Un jeu de données de grande dimension est un jeu de données qui comporte un grand nombre de colonnes (ou de variables). Un tel ensemble de données présente de nombreux défis mathématiques ou informatiques. L’objectif est de réduire les dimensions avec des techniques de réduction de dimension.

Contenus
ToggleTechniques de réduction de dimension basés sur le PCA
La bonne nouvelle est que les variables (ou appelées caractéristiques) sont souvent corrélées – les données de grande dimension sont dominées « superficiellement » par un petit nombre de variables simples.
Nous pouvons trouver un sous-ensemble de variables pour représenter le même niveau d’information dans les données ou transformer les variables en un nouvel ensemble de variables sans perdre beaucoup d’informations. Bien que le calcul haute puissance puisse d’une manière ou d’une autre gérer des données de grande dimension, dans de nombreuses applications, il est toujours nécessaire de réduire la dimensionnalité des données d’origine.
L’analyse en composantes principales (ACP) est probablement la technique la plus populaire lorsque l’on pense à la réduction de dimension. Dans cet article, je commencerai par l’ACP, puis je présenterai d’autres techniques de réduction de dimension. Le code Python sera inclus dans chaque technique.
Les data scientists peuvent utiliser des techniques de réduction de dimension pour identifier les anomalies. Pourquoi? Ne voulons-nous pas simplement réduire la dimensionnalité ? L’intuition réside dans les valeurs aberrantes elles-mêmes. D.M.Hawkins a déclaré : « Une valeur aberrante est une observation qui s’écarte tellement des autres observations qu’elle éveille des soupçons qu’elle a été générée par un mécanisme différent. Une fois que les dimensions sont réduites à moins de dimensions principales, les modèles sont identifiés, puis les valeurs aberrantes sont révélées.
Analyse en composantes principales ACP (principal component analysis PCA)
L’idée de l’analyse en composantes principales (ACP) est de réduire la dimensionnalité d’un ensemble de données composé d’un grand nombre de variables liées tout en conservant autant de variance dans les données que possible. L’ACP trouve un ensemble de nouvelles variables dont les variables d’origine ne sont que leurs combinaisons linéaires. Les nouvelles variables sont appelées composantes principales (PC). Ces composantes principales sont orthogonales : dans un cas 3D, les composantes principales sont perpendiculaires entre elles. X ne peut pas être représenté par Y ou Y ne peut pas être représenté par Z.
La figure suivante montre l’intuition de l’ACP : elle « fait pivoter » les axes pour mieux s’aligner avec vos données. La première composante principale captera la majeure partie de la variance des données, suivie de la deuxième, de la troisième, etc. Par conséquent, les nouvelles données auront moins de dimensions.

Let’s use the iris dataset to illustrate PCA:
# Use the iris dataset to illustrate PCA:
import pandas as pd
url = “https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
# load dataset into Pandas DataFrame
df = pd.read_csv(url, names=[‘sepal length’,’sepal width’,’petal length’,’petal width’,’target’])
df.head()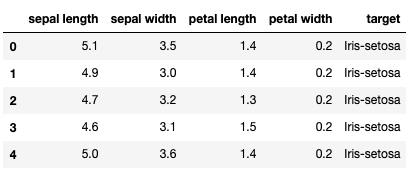
Notez que cet ensemble de données IRIS est fourni avec la variable cible. Dans PCA, vous ne transformez que les variables X sans la variable Y cible.
Toutes les variables doivent être sur la même échelle avant d’appliquer l’ACP, sinon, une caractéristique avec de grandes valeurs dominera le résultat.
Ci-dessous, j’utilise StandardScaler dans scikit-learn pour standardiser les caractéristiques de l’ensemble de données sur l’échelle unitaire (moyenne = 0 et variance = 1).
from sklearn.preprocessing import StandardScaler
variables = [‘sepal length’, ‘sepal width’, ‘petal length’, ‘petal width’]
x = df.loc[:, variables].values
y = df.loc[:,[‘target’]].values
x = StandardScaler().fit_transform(x)
x = pd.DataFrame(x)
Il y a quatre caractéristiques dans les données d’origine. PCA fournira donc le même nombre de composants principaux.
from sklearn.decomposition import PCA
pca = PCA()
x_pca = pca.fit_transform(x)
x_pca = pd.DataFrame(x_pca)
x_pca.head()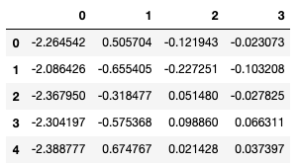
Quelles sont les variances expliquées par chacune des composantes principales ? Utilisez pca.explained_variance_ratio_ pour renvoyer un vecteur de la variance :
explained_variance = pca.explained_variance_ratio_
explained_variancearray([0.72770452, 0.23030523, 0.03683832, 0.00515193])
Il montre que la première composante principale représente une variance de 72,22 %, les deuxième, troisième et quatrième représentent respectivement une variance de 23,9 %, 3,68 % et 0,51 %. Nous pouvons dire que 72,22 + 23,9 = 96,21% de l’information est capturée par les première et deuxième composantes principales.
Nous voulons souvent ne garder que les fonctionnalités significatives et supprimer les insignifiantes. Une règle empirique consiste à conserver les principales composantes principales qui captent une variance importante et à ignorer les petites.
Nous pouvons tracer les résultats en utilisant les deux premières composantes. Ajoutons la variable cible y aux nouvelles données x_pca :
x_pca[‘target’]=y
x_pca.columns = [‘PC1’,’PC2',’PC3',’PC4',’target’]
x_pca.head()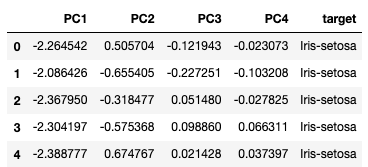
Le résultat montre que les données sont séparables dans le nouvel espace.
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.set_xlabel(‘Principal Component 1’)
ax.set_ylabel(‘Principal Component 2’)
ax.set_title(‘2 component PCA’)
targets = [‘Iris-setosa’, ‘Iris-versicolor’, ‘Iris-virginica’]
colors = [‘r’, ‘g’, ‘b’]
for target, color in zip(targets,colors):
indicesToKeep = x_pca[‘target’] == target
ax.scatter(x_pca.loc[indicesToKeep, ‘PC1’]
, x_pca.loc[indicesToKeep, ‘PC2’]
, c = color
, s = 50)
ax.legend(targets)
ax.grid()
Comment utilisons-nous l’ACP pour détecter les valeurs aberrantes ? Laissez-moi vous donner l’intuition. Après la transformation, les points de données « normaux » s’aligneront le long des vecteurs propres (nouveaux axes) avec de petites valeurs propres. Les valeurs aberrantes sont éloignées des vecteurs propres avec de grandes valeurs propres. Par conséquent, les distances entre chaque point de données et les vecteurs propres deviennent une mesure de la valeur aberrante. Une grande distance indique une anomalie.
Kernel ACP (KPCA)
L’ACP applique la transformation linéaire, qui n’est que sa limitation. KACP étend l’ACP à la non-linéarité. Il mappe d’abord les données d’origine sur un espace d’entités non linéaires (généralement de dimension supérieure), puis applique l’ACP pour extraire les composants principaux de cet espace. Ceci peut être compris par la figure (B). Le graphique de gauche montre que les points bleus et rouges ne peuvent pas être séparés à l’aide d’une transformation linéaire. Mais si tous les points sont projetés sur un espace 3D, le résultat devient linéairement séparable ! Nous appliquons ensuite PCA pour séparer les composants.
D’où vient l’intuition ? Pourquoi la séparation des composants devient-elle plus facile dans un espace de dimension supérieure ? Cela doit remonter à la théorie de Vapnik-Chervonenkis (VC). Il dit que la cartographie dans un espace de dimension supérieure fournit souvent une plus grande puissance de classification.

Le code Python suivant crée un tracé circulaire composé de points rouges et bleus. Évidemment, il n’y a aucun moyen de séparer les points rouges et bleus avec une ligne (séparation linéaire).
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA, KernelPCA
from sklearn.datasets import make_circlesnp.random.seed(0)
X, y = make_circles(n_samples=400, factor=.3, noise=.05)plt.figure(figsize=(10,10))
plt.subplot(2, 2, 1, aspect='equal')
plt.title("Original space")
reds = y == 0
blues = y == 1plt.scatter(X[reds, 0], X[reds, 1], c="red",s=20, edgecolor='k')
plt.scatter(X[blues, 0], X[blues, 1], c="blue",s=20, edgecolor='k')
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
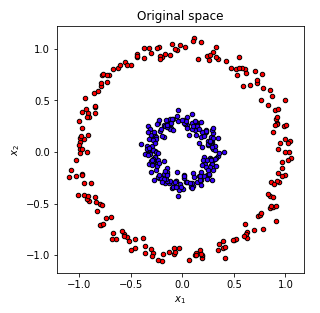
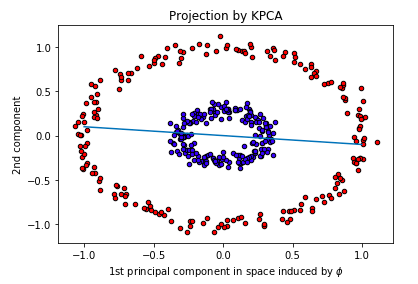
Cependant, lorsque nous projetons le cercle dans un espace de dimension supérieure et que nous séparons à l’aide de l’ACP, les observations de données par rapport aux première et deuxième composantes principales sont séparables ! Vous trouverez ci-dessous le résultat que les points sont tracés par rapport aux première et deuxième composantes principales. Je trace une ligne pour séparer les points rouges et bleus.
Dans KernelPCA, nous spécifions kernel=’rbf’, qui est la fonction de base radiale, ou la distance euclidienne. Les RBF sont couramment utilisés comme noyau dans les techniques d’apprentissage automatique telles que la machine à vecteurs de support (SVM).
kpca = KernelPCA(kernel=”rbf”, fit_inverse_transform=True, gamma=10)
X_kpca = kpca.fit_transform(X)
pca = PCA()
X_pca = pca.fit_transform(X)plt.scatter(X_kpca[reds, 0], X_kpca[reds, 1], c=”red”,s=20, edgecolor=’k’)
plt.scatter(X_kpca[blues, 0], X_kpca[blues, 1], c=”blue”,s=20, edgecolor=’k’)
x = np.linspace(-1, 1, 1000)
plt.plot(x, -0.1*x, linestyle=’solid’)
plt.title(“Projection by KPCA”)
plt.xlabel(r”1st principal component in space induced by $\phi$”)
plt.ylabel(“2nd component”)

Si nous spécifions que le noyau est « linéaire » comme le code ci-dessous (KernelPCA(kernel=’linear’), il devient le PCA standard avec seulement une transformation linéaire, et les points rouges et bleus ne sont pas séparables.
kpca = KernelPCA(kernel=”linear”, fit_inverse_transform=True, gamma=10)
X_kpca = kpca.fit_transform(X)
pca = PCA()
X_pca = pca.fit_transform(X)plt.scatter(X_kpca[reds, 0], X_kpca[reds, 1], c=”red”,s=20, edgecolor=’k’)
plt.scatter(X_kpca[blues, 0], X_kpca[blues, 1], c=”blue”,s=20, edgecolor=’k’)
x = np.linspace(-1, 1, 1000)
plt.plot(x, -0.1*x, linestyle=’solid’)
plt.title(“Projection by KPCA”)
plt.xlabel(r”1st principal component in space induced by $\phi$”)
plt.ylabel(“2nd component”)
Analyse Discriminante Linéaire ADL (Linear Discriminant Analysis LDA)
L’origine de LDA est différente de PCA. L’ACP est une méthode d’apprentissage non supervisée qui transforme les fonctionnalités d’origine en un ensemble de nouvelles fonctionnalités. Nous ne nous soucions pas de savoir si le nouvel ensemble de caractéristiques peut fournir le meilleur pouvoir discriminant pour la variable cible. En revanche, l’analyse discriminante linéaire (LDA) cherche à préserver autant de pouvoir discriminant que possible pour la variable dépendante, tout en projetant la matrice de données d’origine sur un espace de dimension inférieure.
LDA est un type de technique d’apprentissage supervisé. Il utilise les classes de la variable dépendante pour diviser l’espace des prédicteurs en régions. Toutes les régions devraient avoir des limites linéaires. D’où le nom linéaire vient. Le modèle prédit que toutes les observations d’une région appartiennent à la même classe de la variable dépendante.
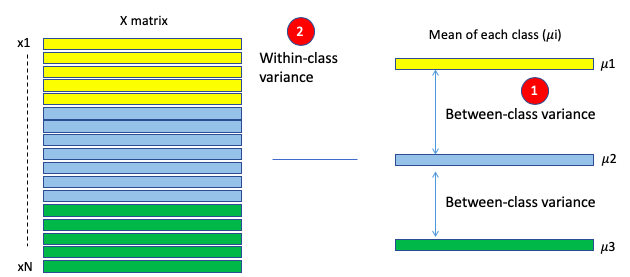
LDA atteint l’objectif ci-dessus en trois étapes principales. Tout d’abord, il calcule la séparabilité entre les différentes classes de la variable dépendante, appelée variance entre les classes, comme indiqué en (1) de la figure LDA. Deuxièmement, il calcule la distance entre la moyenne et les échantillons de chaque classe, appelée variance intra-classe, comme indiqué dans (2). Ensuite, il construit l’espace de dimension inférieure avec ce critère : maximiser la variance inter-classes et minimiser la variance intra-classe.
La solution à ce critère est de calculer les valeurs propres et les vecteurs propres. Les vecteurs propres résultants représentent les directions du nouvel espace et les valeurs propres correspondantes représentent la longueur des vecteurs propres. Ainsi, chaque vecteur propre représente un axe de l’espace LDA, et la valeur propre représente la longueur de ce vecteur propre.
J’utiliserai l’ensemble de données « Qualité du vin rouge » dans le cadre du concours Kaggle. Cet ensemble de données a 11 variables d’entrée et une variable de sortie « qualité ».
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
wine = pd.read_csv(‘winequality-red.csv’)
wine.head()
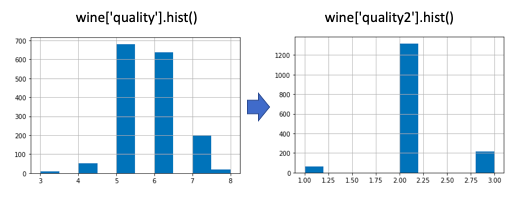
Par souci de simplicité, je regroupe la variable de sortie en trois valeurs. wine[‘quality2’] = np.where(wine[‘quality’]<=4,1, np.where(wine[‘quality’]<=6,2,3)).
Le code suivant exécute PCA et LDA.
X = wine.drop(columns=[‘quality’,’quality2'])
y = wine[‘quality2’]
target_names = np.unique(y)
target_namespca = PCA(n_components=2)
X_r = pca.fit(X).transform(X)lda = LinearDiscriminantAnalysis(n_components=2)
X_r2 = lda.fit(X, y).transform(X)
Ensuite, tracez les résultats de PCA et LDA :
# Percentage of variance explained for each components
print(‘explained variance ratio (first two components): %s’
% str(pca.explained_variance_ratio_))plt.figure()
colors = [‘navy’, ‘turquoise’, ‘darkorange’]
lw = 2for color, i, target_name in zip(colors, target_names, target_names):
plt.scatter(X_r[y == i, 0], X_r[y == i, 1], color=color, alpha=.8, lw=lw,
label=target_name)
plt.legend(loc=’best’, shadow=False, scatterpoints=1)
plt.title(‘PCA of WINE dataset’)plt.figure()
for color, i, target_name in zip(colors, target_names, target_names):
plt.scatter(X_r2[y == i, 0], X_r2[y == i, 1], alpha=.8, color=color,
label=target_name)
plt.legend(loc=’best’, shadow=False, scatterpoints=1)
plt.title(‘LDA of WINE dataset’)plt.show()

LDA convient à un problème de classification multi-classes.
Décomposition en valeurs singulières (Singular Value Decomposition SVD)
SVD est une méthode de synthèse des données similaire à l’ACP. Il extrait les caractéristiques importantes des données. Mais il y a un autre avantage de SVD : reconstruire l’ensemble de données d’origine en un petit ensemble de données. Il a donc de larges applications telles que la compression d’images. Par exemple, si vous avez une image 32*32 = 1 024 pixels, SVD peut la résumer en 66 pixels. Les 66 pixels peuvent récupérer des images de 32*32 pixels sans manquer aucune information importante.
SVD a joué un rôle déterminant dans l’algèbre linéaire, mais il semble « pas aussi célèbre qu’il devrait l’être » comme indiqué dans le manuel classique « L’algèbre linéaire et ses applications » de Gilbert Strang. Pour bien introduire SVD, il est indispensable de commencer par le fonctionnement matriciel. Si A est une matrice réelle n × n symétrique, il existe une matrice orthogonale V et une diagonale D telles que

Les colonnes V sont des vecteurs propres pour A et les entrées diagonales de D sont les valeurs propres de A. Ce processus s’appelle la décomposition des valeurs propres, ou EVD, pour la matrice A. Il nous indique comment choisir des bases orthonormales de sorte que la transformation soit représentée par une matrice. avec la forme la plus simple possible, c’est-à-dire en diagonale. (Pour les lecteurs qui souhaitent passer en revue les étapes de diagonalisation d’une matrice, voici un bon exemple.) Le terme orthonormal signifie que deux vecteurs sont orthogonaux ou perpendiculaires.
En étendant la matrice symétrique, le SVD fonctionne avec n’importe quelle matrice A réelle m × n. Étant donné une matrice A réelle m × n, il existe une matrice orthogonale m × m U, une matrice orthogonale m × m V et une diagonale m × n matrice Σ telle que
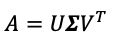
Notez qu’une matrice orthogonale est une matrice carrée telle que le produit d’elle-même et de sa matrice inverse est une matrice identité. Une matrice diagonale est une matrice dans laquelle les entrées autres que la diagonale sont toutes nulles.
Ci-dessous, j’utiliserai à nouveau l’ensemble de données d’iris pour vous montrer comment appliquer SVD.
from numpy import *
import operator
import matplotlib.pyplot as plt
import pandas as pd
from numpy.linalg import *url = “https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
# load dataset into Pandas DataFrame
df = pd.read_csv(url, names=[‘sepal length’,’sepal width’,’petal length’,’petal width’,’target’])# Only the X variables
data = df[[‘sepal length’,’sepal width’,’petal length’,’petal width’]]#calculate SVD
n = 2 # We will take two Singular Values
U, s, V = linalg.svd( data )# eye() creates a matrix with ones on the diagonal and zeros elsewhere
Sig = mat(eye(n)*s[:n])
newdata = U[:,:n]
newdata = pd.DataFrame(newdata)
newdata.columns=[‘SVD1’,’SVD2']
newdata.head()
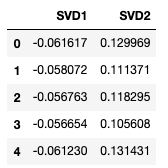
Vous pouvez comparer le résultat de SVD à celui de PCA. Les deux obtiennent des résultats similaires.
# Add the actual target to the data in order to plot it
newdata[‘target’]=df[‘target’]fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.set_xlabel(‘SVD 1’)
ax.set_ylabel(‘SVD 2’)
ax.set_title(‘SVD’)
targets = [‘Iris-setosa’, ‘Iris-versicolor’, ‘Iris-virginica’]
colors = [‘r’, ‘g’, ‘b’]
for target, color in zip(targets,colors):
indicesToKeep = newdata[‘target’] == target
ax.scatter(newdata.loc[indicesToKeep, ‘SVD1’]
, newdata.loc[indicesToKeep, ‘SVD2’]
, c = color
, s = 50)
ax.legend(targets)
ax.grid()

Encastrement du voisin stochastique distribué en t (t-SNE)
t-SNE est développé par Laurens van der Maaten et Geoggrey Hinton. Il s’agit d’un algorithme d’apprentissage automatique pour la visualisation qui présente l’intégration de données de grande dimension dans un espace de faible dimension à deux ou trois dimensions.
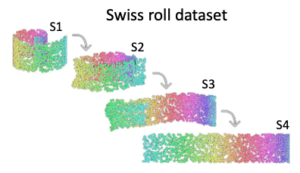
Quelle est la meilleure façon de présenter le rouleau suisse tridimensionnel ci-dessus en bidimensionnel ? Intuitivement, nous voulons « dérouler » le rouleau suisse en un gâteau plat. En mathématiques, cela signifie que des points similaires deviendront des points proches et que des points dissemblables deviendront des points distants.
La figure suivante montre un autre exemple. C’est un tétraèdre tridimensionnel avec des points de données regroupés dans les coins des sommets. Si nous réduisons simplement le graphique tridimensionnel à un graphique bidimensionnel comme le fait le panneau (A), cela ne fonctionne pas bien car le groupe (A) devient le cluster central. En revanche, le panneau (B) est probablement une meilleure exposition 2D qui préserve les distances éloignées entre le groupe (A) – (E) tout en conservant les distances locales des points dans chaque groupe. t-SNE, une technique de réduction de dimension non linéaire, est conçue pour préserver les voisinages locaux. Si un ensemble de points se regroupent sur un tracé t-SNE, nous pouvons être assez certains que ces points sont proches les uns des autres.
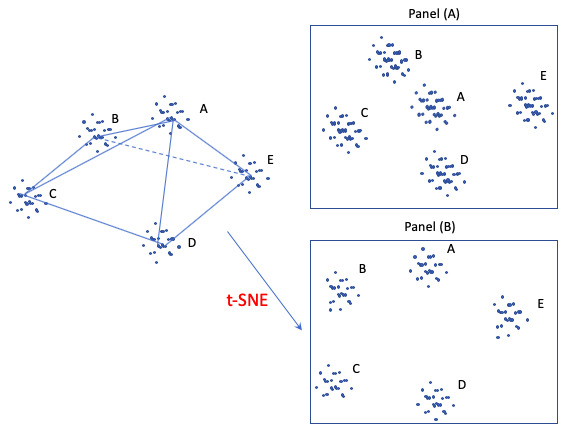
t-SNE modélise les similitudes entre les points. Comment définit-il les similitudes ? Premièrement, il est défini par la distance euclidienne entre le point Xi et Xj. Deuxièmement, il est défini comme la probabilité conditionnelle que « la similarité du point de données i au point j est la probabilité conditionnelle p que le point i choisisse les données j comme son voisin si d’autres voisins étaient sélectionnés en fonction de leurs probabilités sous une distribution gaussienne ». Dans l’expression conditionnelle suivante, si le point j est plus proche du point i que d’autres points, il a une probabilité plus élevée (notez le signe négatif) d’être choisi.
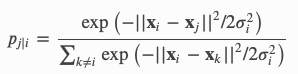
t-SNE vise à faire correspondre la probabilité conditionnelle ci-dessus p entre j et i aussi bien que possible par un espace de faible dimension q entre le point Yi et Yj, comme indiqué ci-dessous. La probabilité q suit une distribution Student-t à queue grasse, d’où provient le « t » dans t-SNE.
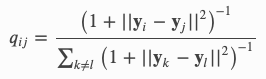
L’étape suivante consiste à trouver Yi de sorte que la distribution q se rapproche le plus possible de la distribution p . t-SNE utilise la technique de descente de gradient, une technique d’optimisation, pour trouver les valeurs.
Ci-dessous, je montre comment la technique t-SNE est utilisée avec l’ensemble de données de l’iris.
from sklearn.manifold import TSNE
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
iris = load_iris()
X_tsne = TSNE(learning_rate=100).fit_transform(iris.data)
X_pca = PCA().fit_transform(iris.data)
plt.figure(figsize=(10, 5))
plt.subplot(121)
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=iris.target)
plt.subplot(122)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=iris.target)
