Cette page montre plusieurs exemples sur les cas d’usage des différentes moyenne, notamment la moyenne géométrique et la moyenne harmonique.

Contenus
ToggleMoyenne arithmétique
La moyenne arithmétique est nommée de manière appropriée : nous la trouvons en ajoutant tous les nombres de l’ensemble de données, puis en divisant par le nombre de nombres dans l’ensemble de données (afin de ramener la somme à l’échelle des nombres d’origine).
3 + 8 + 10 = 21
21 ÷ 3 = 7
Arithmetic mean = 7
Remarquez, ce que nous disons essentiellement ici est : si chaque nombre de notre ensemble de données était le même nombre, quel nombre devrait-il être pour avoir la même somme que notre ensemble de données réel ?
Mais il n’y a rien de particulièrement spécial dans l’addition. C’est juste une opération mathématique assez simple. La moyenne arithmétique fonctionne bien pour produire un nombre « moyen » d’un ensemble de données lorsqu’il existe une relation additive entre les nombres.
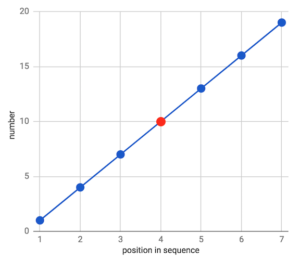
Une telle relation est souvent appelée « linéaire », car lorsqu’ils sont représentés graphiquement dans l’ordre croissant ou décroissant, les nombres ont tendance à tomber sur ou autour d’une ligne droite. Un exemple idéalisé simple serait un ensemble de données où chaque nombre est produit en ajoutant 3 au nombre précédent :
1, 4, 7, 10, 13, 16, 19…

La moyenne arithmétique nous donne donc une valeur médiane parfaitement raisonnable :
(1 + 4 + 7 + 10 + 13 + 16 + 19) ÷ 7 = 10
Mais tous les ensembles de données ne sont pas mieux décrits par cette regression linéaire. Certains ont une relation multiplicative ou exponentielle, par exemple si nous multiplions chaque nombre consécutif par 3 plutôt que d’additionner par 3 comme nous l’avons fait ci-dessus :
1, 3, 9, 27, 81, 243, 729…
Cela produit ce que l’on appelle une série géométrique. Lorsqu’ils sont tracés dans l’ordre, ces nombres ressemblent plus à une courbe qu’à une ligne droite.
Dans cette situation, la moyenne arithmétique est mal adaptée pour produire un nombre « moyen » pour résumer ces données.
(1 + 3 + 9 + 27 + 81 + 243 + 729) ÷ 7 = 156.1
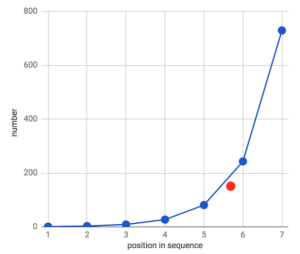
156 n’est pas particulièrement proche de la plupart des chiffres de notre ensemble de données. En fait, c’est plus de 5 x la médiane (chiffre du milieu), qui est de 27.
Que faire dans ce cas là ?
La moyenne géométrique
Puisque la relation est multiplicative, pour trouver la moyenne géométrique, nous multiplions plutôt que d’additionner tous les nombres. Ensuite, pour redimensionner le produit à la plage de l’ensemble de données, nous devons prendre la racine du nombre d’élément, plutôt que de simplement diviser.
Ainsi, la moyenne géométrique de notre jeu de données est :
1 * 3 * 9 * 27 * 81 * 243 * 729 = 10,460,353,203
7th root of 10,460,353,203 = 27
geometric mean = 27
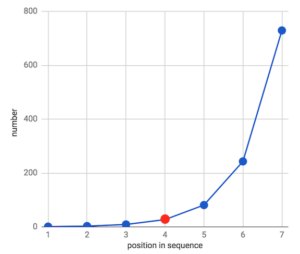
Dans ce cas, notre moyenne géométrique ressemble beaucoup à la valeur médiane de notre ensemble de données. En fait, il équivaut à la médiane.
La moyenne géométrique ne sera pas toujours égale à la médiane, uniquement dans les cas où il existe une relation multiplicative exacte et cohérente entre tous les nombres (par exemple, en multipliant chaque nombre précédent par 3, comme nous l’avons fait).
Les ensembles de données du monde réel contiennent rarement des relations aussi exactes, mais pour ceux qui se rapprochent de ce type de relation multiplicative, la moyenne géométrique donnera un « nombre médian » plus proche que la moyenne arithmétique.
Exemple de moyenne géométrique
Supposons que nous disposions de 100 000 $ qui génèrent un taux d’intérêt variable chaque année pendant 5 ans :
annual interest rates: 1%, 9%, 6%, 2%, 15%
Nous aimerions prendre un raccourci pour trouver notre taux d’intérêt annuel moyen, et donc notre montant total d’argent après 5 ans, alors nous essayons de « faire la moyenne » de ces taux :
(.01 + .09 + .06 + .02 + .15) ÷ 5 = .066 = 6.6%
Ensuite, nous insérons ce pourcentage moyen dans une formule d’intérêt composé :
Total interest earned = $100,000 * (1.066⁵ - 1) = $37,653.11
Interest + principal = $37,653.11 + 100,000 = $137,653.11
Final total = $137,653.11
Comparons les résultats :
Year 1: 100,000 + (100,000 * .01) = 100,000 * 1.01 = $101,000Year 2: 101,000 * 1.09 = $110,090Year 3: 110,090 * 1.06 = $116,695.40Year 4: 116,695.40 * 1.02 = $119,029.31Year 5: 119,029.31 * 1.15 = $136,883.70Actual final total = $136,883.70
Notre raccourci a surestimé nos revenus réels de près de 1 000 $.
Nous avons fait une erreur courante : nous avons appliqué une opération additive à un processus multiplicatif et obtenu un résultat inexact.
Essayons à nouveau avec la moyenne géométrique :
1.01 * 1.09 * 1.06 * 1.02 * 1.15 = 1.368837042
5th root of 1.368837042 = 1.064805657
Geometric mean = 1.064805657
Brancher la moyenne géométrique des taux d’intérêt dans notre formule d’intérêt composé :
Total interest earned = $100,000 * (1.0648⁵ - 1) = $36,883.70
Interest + principal = $36,883.70 + 100,000 = $136,883.70
Final total = $136,883.70 exactly the same as the long method above
Ce qui correspond à la réalité !
Moyenne géométrique et changement d'échelle
Une caractéristique intéressante de la moyenne géométrique est que vous pouvez en fait faire la moyenne de nombres sur des échelles complètement différentes.
Par exemple, nous voulons comparer les notes en ligne de deux coffeeshops en utilisant deux sources différentes. Le problème est que la source 1 utilise une échelle de 5 étoiles et la source 2 utilise une échelle de 100 points :
Coffeeshop A
source 1rating:4.5source 2rating:68Coffeeshop B
source 1rating:3source 2rating:75
Si l’on prend naïvement la moyenne arithmétique des notes brutes de chaque coffeeshop :
Coffeeshop A =
(4.5 + 68) ÷ 2 = 36.25Coffeeshop B =(3 + 75) ÷ 2 = 39
Nous en conclurions que le Coffeeshop B était le gagnant.
Si nous connaissions un peu mieux les chiffres, nous saurions que nous devons normaliser nos valeurs sur la même échelle avant d’en faire la moyenne avec la moyenne arithmétique, pour obtenir un résultat précis. Nous multiplions donc les notes de la source 1 par 20 pour les faire passer d’une échelle de 5 étoiles à l’échelle de 100 étoiles de la source 2 :
Coffeeshop A
4.5 * 20 = 90
(90 + 68) ÷ 2 = 79Coffeeshop B
3 * 20 = 60
(60 + 75) ÷ 2 = 67.5
Nous constatons donc que Coffeeshop A est le vrai gagnant, contrairement à l’application naïve de la moyenne arithmétique ci-dessus.
La moyenne géométrique, cependant, nous permet d’arriver à la même conclusion sans avoir à nous soucier de l’échelle ou des unités de mesure :
Coffeeshop A =
square root of (4.5 * 68) = 17.5Coffeeshop B =square root of (3 * 75) = 15
Et voilà !
La moyenne arithmétique est dominée par des nombres à plus grande échelle, ce qui nous fait penser que Coffeeshop B est le magasin le mieux noté. En effet, la moyenne arithmétique attend une relation additive entre les nombres et ne tient pas compte des échelles et des proportions. D’où la nécessité de mettre les nombres sur la même échelle avant d’appliquer la moyenne arithmétique.
La moyenne géométrique, en revanche, peut facilement gérer des proportions variables, en raison de sa nature multiplicative. C’est une propriété extrêmement utile, mais remarquez ce que nous perdons : nous n’avons plus du tout d’échelle interprétable. La moyenne géométrique est effectivement sans unité dans de telles situations.
Et la moyenne harmonique ?
Alors que la moyenne arithmétique nécessite une addition et que la moyenne géométrique utilise une multiplication, la moyenne harmonique utilise des inverses.
Comme vous vous en souvenez peut-être, l’inverse d’un nombre n est simplement 1 / n. (par exemple, l’inverse de 5 est 1/5). Pour les nombres qui sont déjà des fractions, cela signifie que vous pouvez simplement « inverser » le numérateur et le dénominateur : inverse de 4/5 = 5/4. Cela est vrai car 1 divisé par une fraction donne l’inverse de cette fraction, par ex. 1 ÷ (4/5) = 5/4.
Ainsi, la moyenne harmonique peut être décrite avec des mots : l’inverse de la moyenne arithmétique des inverses de l’ensemble de données.
Ce ne sont en fait que quelques étapes simples :
1. Take the reciprocal of all numbers in the dataset
2. Find the arithmetic mean of those reciprocals
3. Take the reciprocal of that number
En notation mathématique, cela ressemble à :

La moyenne harmonique de 1, 4 et 4 est 2.
Remarque : du fait que 0 n’a pas d’inverse (rien ne peut être multiplié par 0 pour = 1), la moyenne harmonique ne peut pas non plus gérer les ensembles de données contenant des 0, comme la moyenne géométrique.
Mais à quoi ça sert ?
Exemple de moyenne harmonique
Encore une fois, similaire à l’utilisation de la moyenne géométrique comme contrepartie de la moyenne arithmétique pour les relations multiplicatives ou non linéaires, la moyenne harmonique nous aide à trouver des relations multiplicatives/divisantes entre les fractions sans nous soucier des dénominateurs communs.
En tant que telle, la moyenne harmonique accepte naturellement une autre couche de multiplication/division sur la moyenne géométrique. Il est donc utile lorsqu’il s’agit d’ensembles de données de taux ou de ratios (c’est-à-dire de fractions) sur différentes longueurs ou périodes.
L’exemple canonique de l’utilisation de moyens harmoniques dans le monde réel implique de voyager dans l’espace physique à différentes vitesses, c’est-à-dire des vitesses.
Envisagez un voyage à l’épicerie et retour :
- Sur le chemin, vous avez conduit 30 mph tout le trajet
- Sur le chemin du retour, la circulation était lente et vous avez conduit 16 km/h tout le trajet
- Vous avez emprunté le même itinéraire et couvert la même quantité de terrain (5 miles) dans chaque sens.
Quelle a été votre vitesse moyenne sur toute la durée de ce trajet ?
Encore une fois, nous pourrions naïvement appliquer la moyenne arithmétique à 30 mph & 10 mph, et déclarer fièrement « 20 mph ! »
Étant donné que vous avez voyagé plus vite dans une direction, vous avez parcouru ces 8 km plus rapidement et passé moins de temps à voyager à cette vitesse, de sorte que votre vitesse de déplacement moyenne sur l’ensemble de la durée de votre voyage n’est pas le point médian entre 30 mph et 10 mph, il devrait être plus près de 10 mph parce que vous avez passé plus de temps à rouler à cette vitesse.
Afin d’appliquer correctement la moyenne arithmétique ici, nous devons déterminer le temps passé à voyager à chaque tarif, puis pondérer notre calcul de moyenne arithmétique de manière appropriée :
Trip There: (at 30 mph)
30 miles per 60 mins = 1 mile every 2 minutes = 1/2 mile every minute
5 miles at 1/2 mile per minute = 5 ÷ 1/2 = 10 minutes
"Trip There" time = 10 minutes
Trip Back: (at 10 mph)
10 miles per 60 mins = 1 mile every 6 minutes = 1/6 miles every minute
5 miles at 1/6 mile per minute = 5 ÷ 1/6 = 30 minutes
"Trip Back" time = 30 minutes
Total trip time = 10 + 30 = 40 minutes
“Trip There” % of total trip = 10 / 40 minutes = .25 = 25%
“Trip Back” % of total trip = 30 / 40 minutes = .75 = 75%
Weighted Arithmetic Mean = (30mph * .25)+(10mph * .75) = 7.5 + 7.5 = 15
Average rate of travel = 15 mph
Nous voyons donc que notre véritable taux moyen de déplacement était 15 mph, ce qui est 5 mph (ou 25 %) inférieur à notre déclaration naïve de 20 mph en utilisant une moyenne arithmétique non pondérée.
Essayons à nouveau en utilisant la moyenne harmonique.
Harmonic mean of 30 and 10 = ...
Arithmetic mean of reciprocals = 1/30 + 1/10 = 4/30 ÷ 2 = 4/60 = 1/15
Reciprocal of arithmetic mean = 1 ÷ 1/15 = 15/1 = 15
Et voilà !
