Contenus
ToggleRéseau de Hopfield
Dans un réseau de Hopfield, au cours du processus de formation, on peut penser que les poids dans le réseau minimisent une fonction énergétique et glissent sur une surface d’énergie. Dans un réseau entrainé, chaque modèle présenté au réseau fournit un attracteur, où des progrès sont réalisés vers le point d’attraction en propageant des informations autour du réseau.
L’objectif de traitement de l’information du système est d’associer les composants d’un modèle d’entrée à une représentation holistique du modèle appelé Content Addressable Memory (CAM). Cela signifie qu’une fois formé, le système rappellera des motifs entiers ou une version bruyante du motif d’entrée.
Le réseau de Hopfield comprend une structure de données en graphe avec des arêtes pondérés et des procédures distinctes pour la formation et l’application de la structure. La structure du réseau est entièrement connectée (un nœud se connecte à tous les autres nœuds sauf lui-même) et les arêtes (poids) entre les nœuds sont bidirectionnels.
Les poids du réseau peuvent être appris via une méthode en one-shot (une itération sur tous les modèles) si tous les modèles à mémoriser par le réseau sont connus. Alternativement, les poids peuvent être mis à jour de manière incrémentielle en utilisant la règle Hebb où les poids sont augmentés ou diminués en fonction de la différence entre la sortie réelle et la sortie attendue. Le calcul ponctuel des poids de réseau pour un seul nœud se produit comme suit:

où w_i, j est le poids entre le neurone i et j, N est le nombre de modèles d’entrée, v est le modèle d’entrée et v_ik est le i-ème attribut sur le k-ème modèle d’entrée.
La propagation des informations à travers le réseau peut être asynchrone où un nœud aléatoire est sélectionné à chaque itération, ou de manière synchrone, où la sortie est calculée pour chaque nœud avant d’être appliquée à l’ensemble du réseau. La propagation des informations se poursuit jusqu’à ce qu’aucune autre modification ne soit effectuée ou jusqu’à ce qu’un nombre maximal d’itérations soit terminé, après quoi le modèle de sortie du réseau peut être lu. L’activation pour un seul nœud est calculée comme suit:
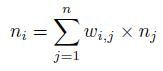
où n_i est l’activation du i-ème neurone, w_i, j avec le poids entre les nœuds i et j, et n_j est la sortie du j-ème neurone. L’activation est transférée dans une sortie à l’aide d’une fonction de transfert, généralement une fonction à pas comme suit:
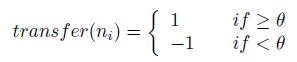
où le seuil θ est généralement fixé à 0.
Le réseau de Hopfield peut être utilisé pour résoudre le problème de rappel des correspondances de repères pour un motif d’entrée à un motif pré-appris associé.
La fonction de transfert pour transformer l’activation d’un neurone en sortie est typiquement une fonction à pas f(a) dans {-1, 1} (préférée), ou plus traditionnellement f(a) dans {0, 1}. Les vecteurs d’entrée sont généralement normalisés aux valeurs booléennes x dans [-1; 1].
Le réseau peut être propagé de manière asynchrone (où un nœud aléatoire est sélectionné et généré en sortie), ou de manière synchrone (où la sortie de tous les nœuds est calculée avant d’être appliquée).
Les pondérations peuvent être apprises selon une méthode ponctuelle ou incrémentielle en fonction de la quantité d’informations connues sur les modèles à apprendre. Tous les neurones du réseau sont généralement à la fois des neurones d’entrée et de sortie, bien que d’autres topologies de réseau aient été étudiées (comme la désignation des neurones d’entrée et de sortie). Un réseau de Hopfield a des limites sur les modèles qu’il peut stocker et récupérer avec précision à partir de la mémoire, décrite par N<0,15*n où N est le nombre de modèles qui peuvent être stockés et récupérés et n est le nombre de nœuds dans le réseau.
