Contenus
ToggleCritères de qualité internes
Les critères de qualité internes mesurent généralement la compacité des clusters à l’aide d’une mesure de similitude. Il mesure généralement l’homogénéité intra-cluster, la séparabilité inter-cluster ou une combinaison de ces deux. Il n’utilise pas d’informations externes à côté des données elles-mêmes.

Liste
- Somme de l’erreur quadratique
- Critères de dispersion
- Métrique d’utilité de la catégorie
- Mesures de coupe
- Ball-Hall
- Banfeld-Raftery
- Critère de Condorcet
- Critère C
- Calinski-Harabasz
- Davies-Bouldin
- Det_Ratio
- Dunn
- GDImn
- Gamma
- G+
- Ksq_DetW
- Log_Det_Ratio
- Log_SS_Ratio
- McClain-Rao
- PBM
- Point biserial
- Ratkawsky-Lance
- Ray-Turi
- Scott-Symons
- SD_Scat
- SD_Dis
- S_Dbw
- Silhouette
- Trace W
- Trace WiB
- Wemmert-Gançarski
- Xie-Beni
Comment lire les mesures de qualité interne
Afin de trouver la meilleure partition des données, on exécute généralement un algorithme de clustering avec différentes valeurs du nombre attendu de clusters K : disons que Km ≤ K ≤ KM. L’algorithme de clustering appliqué pourrait être un clustering hiérarchique ascendant (AHC) ou l’algorithme k-means ou toute autre technique. On calcule ensuite un indice de qualité QK pour chaque valeur de K et sélectionne la partition qui a conduit à la « meilleure » valeur pour QK.
Cette section explique ce qui est considéré comme la « meilleure » valeur pour les différents indices de qualité.
Le tableau résume, pour chaque indice, quelle règle doit être appliquée afin de déterminer la meilleure valeur d’indice. Par exemple, dans le cas de l’indice de Calinski-Harabasz, si l’indice de qualité a été calculé pour différentes partitions des données, la meilleure partition est celle correspondant à la plus grande valeur de l’indice.
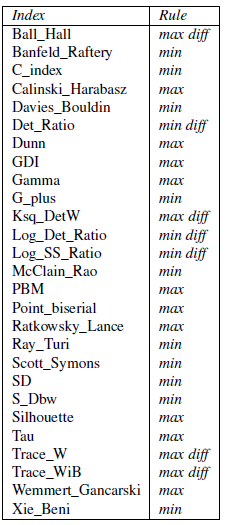
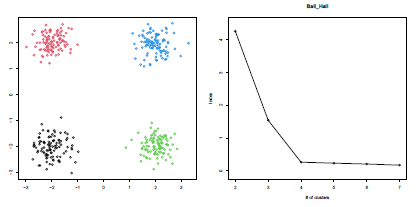
Les règles de décision appelées max et min dans le tableau signifient qu’il faut sélectionner respectivement la plus grande ou la plus petite valeur d’indice. La règle de décision appelée max diff signifie que la meilleure valeur de K est celle correspondant à la plus grande différence entre deux pentes successives. Sur un diagramme représentant les valeurs d’index par rapport au nombre de clusters sélectionnés, cela correspond à un coude.
Somme de l’erreur quadratique
Les métriques de qualité internes mesurent généralement la compacité des clusters à l’aide d’une mesure de similitude (comme la Somme de l’erreur quadratique). Il mesure généralement l’homogénéité intra-cluster, la séparabilité inter-cluster ou une combinaison de ces deux. Il n’utilise pas d’informations externes à côté des données elles-mêmes.
Somme de l’erreur quadratique est la mesure de critère la plus simple et la plus largement utilisée pour le clustering. Il est calculé comme:
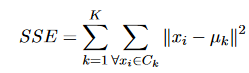
où C_k est l’ensemble des instances du cluster k; μ_k est la moyenne vectorielle du cluster k. Les composantes de μ_k sont calculées comme:
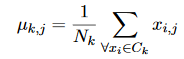
où N_k = | C_k | est le nombre d’instances appartenant au cluster k.
Les méthodes de partitionnement qui minimisent le critère SSE sont souvent appelées partitions de variance minimale, car par simple manipulation algébrique, le critère SSE peut s’écrire:
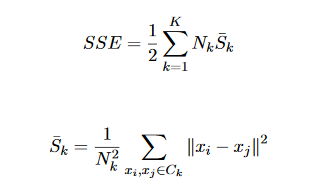
La fonction de critère SSE convient aux cas où les clusters forment des nuages compacts bien séparés les uns des autres.
Des critères minimaux supplémentaires pour SSE peuvent être produits en remplaçant la valeur de S_k par des expressions telles que:
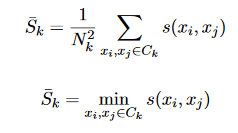
Critères de dispersion
Les métriques de qualité internes mesurent généralement la compacité des clusters à l’aide d’une mesure de similitude (comme les Critères de dispersion : la trace, le déterminant, l’invariance). Il mesure généralement l’homogénéité intra-cluster, la séparabilité inter-cluster ou une combinaison de ces deux. Il n’utilise pas d’informations externes à côté des données elles-mêmes.
Les critères de diffusion scalaire sont dérivés des matrices de diffusion, reflétant la diffusion intra-cluster, la diffusion inter-cluster et leur sommation – la matrice de diffusion totale. Pour le k-ème cluster, la matrice de diffusion peut être calculée comme suit :
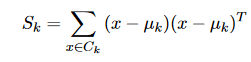
La matrice de dispersion intra-cluster est calculée comme la somme de la dernière définition sur tous les clusters W :

La matrice de diffusion entre clusters peut être calculée comme suit :
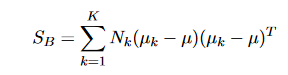
où μ est le vecteur moyen total et est défini comme :

La matrice de diffusion totale doit être calculée comme suit :

Trois critères scalaires peuvent être dérivés de S_W, S_B et S_T.
La trace est la somme des éléments diagonaux d’une matrice. Minimiser la trace de S_W est similaire à minimiser SSE et est donc couramment utilisé. Ce critère, représentant la dispersion intra-cluster, est calculé comme suit :
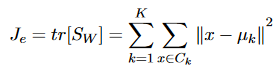
Un autre critère, qui peut être maximisé, est le critère entre les clusters :

Le déterminant d’une matrice de diffusion mesure approximativement le carré du volume de diffusion. Puisque S_B sera singulier si le nombre de clusters est inférieur ou égal à la dimensionnalité, ou si m-c est inférieur à la dimensionnalité, son déterminant n’est pas un critère approprié. Si nous supposons que S_W n’est pas singulier, la fonction du critère de déterminant est :
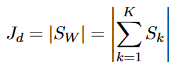
Les valeurs propres λ_1, λ_2,. . . , λ_d de S_W * S_B sont les invariants linéaires de base des matrices de diffusion. Les bonnes partitions sont celles pour lesquelles les valeurs propres non nulles sont grandes. En conséquence, plusieurs critères peuvent être dérivés, y compris les valeurs propres. Trois de ces critères sont :

Uutilitaire de catégorie
L’utilitaire de catégorie est défini comme l’augmentation du nombre attendu de valeurs d’entités pouvant être correctement prédites compte tenu d’un certain regroupement. Cette métrique est utile pour les problèmes qui contiennent un nombre relativement petit de caractéristiques nominales ayant chacune une petite cardinalité.
Mesure de Coupe
Dans certains cas, il est utile de représenter le problème de clustering comme un problème de coupe minimal. Dans de tels cas, la qualité est mesurée comme le rapport des poids restants aux poids coupés totaux. S’il n’y a pas de restriction sur la taille des clusters, il est facile de trouver la valeur optimale. Ainsi, la mesure min-cut est révisée pour pénaliser les structures déséquilibrées.
Ball-Hall
La dispersion moyenne d’un cluster est la moyenne des carrés des distances des points du cluster par rapport à leur barycentre. L’indice Ball-Hall est la moyenne, à travers tous les clusters, de leur dispersion moyenne :
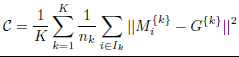
Dans le cas particulier où tous les clusters ont la même taille N/K, cette somme se réduit à WGSS/N.
Banfeld-Raftery
Cet indice est la somme pondérée des logarithmes des traces de la matrice de variance-covariance de chaque cluster.
L’index peut s’écrire ainsi :
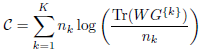
La quantité Tr(WG{k})/nk peut être interprétée comme la moyenne des carrés des distances entre les points du cluster Ck et leur barycentre G{k}. Si un cluster contient un seul point, cette trace est égale à 0 et le logarithme n’est pas défini.
Concordet
Une autre approche appropriée consiste à appliquer la solution de Condorcet au problème de clustering. Dans ce cas, le critère est calculé comme suit:
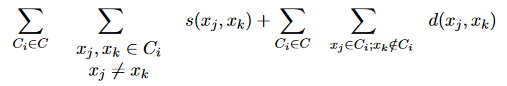
où s (x_j, x_k) et d (x_j, x_k) mesurent la similitude et la distance des vecteurs x_j et x_k.
Critère C
Le critère C est une extension du critère de Condorcet et est défini comme (où γ est une valeur seuil):
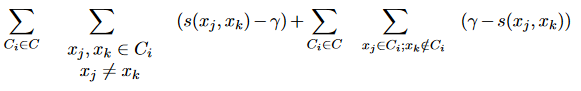
Si l’on considère les distances NT entre paires de points comme une suite de valeurs triées par ordre croissant, l’indice C utilise les plus petites valeurs NW et les valeurs NW les plus grandes pour calculer les sommes Smin et Smax : la somme S implique les distances NW dans cette séquence qui correspondent à des paires présentes dans un cluster (c’est-à-dire des paires dont les deux points sont dans un même cluster). Au maximum, les distances 3NW sont effectivement retenues dans le calcul de cet indice.
Le critère C s’écrit alors ainsi :
![]()
Calinski-Harabasz
Performance basée sur le SSE moyen intra et inter-cluster (Tr):
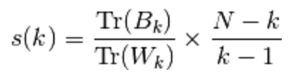
où B_k est la matrice de dispersion entre les clusters et W_k est la matrice de dispersion intra-cluster définie par:
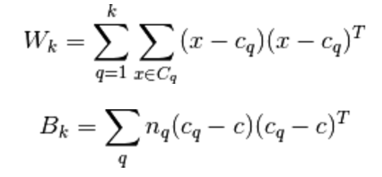
avec N le nombre de points dans nos données, C_q l’ensemble des points du cluster q, c_q le centre du cluster q, c le centre de E, n_q le nombre de points du cluster q.
Davies-Bouldin
Cet indice traite chaque cluster individuellement et cherche à mesurer à quel point elle est similaire au cluster qui lui est le plus proche. L’indice DB est formulé de la façon suivante :
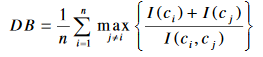
I(c_i) représente la moyenne des distances entre les objets appartenant au cluster C_i et son centre. Et I(c_i,c_j) représente la distance entre les centres des deux clusters C_i et C_j.
Pour chaque cluster i de la partition, on cherche le cluster j qui maximise l’indice décrit comme suit :

La meilleure partition est donc celle qui minimise la moyenne de la valeur calculée pour chaque cluster. En d’autres termes, la meilleure partition est celle qui minimise la similarité entre les clusters.
Det_Ratio
L’index Det_Ratio est défini comme ceci :
![]()
T désigne la matrice de diffusion totale. C’est la somme des matrices BG et WG.
Dunn
L’indice de Dunn est une autre mesure de validation de cluster interne qui peut être calculée comme suit :
- Pour chaque cluster, calculez la distance entre chacun des objets du cluster et les objets des autres clusters
- Utilisez le minimum de cette distance par paire comme séparation inter-cluster (min.separation)
- Pour chaque cluster, calculez la distance entre les objets du même cluster.
- Utilisez la distance maximale intra-cluster (c’est-à-dire le diamètre maximum) comme compacité intra-cluster
- Calculez l’indice de Dunn (D) comme suit :
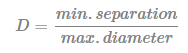
GDImn
L’indice de Dunn généralisé (GDI) donne une valeur basée sur le « bon comportement » des clusters et de leurs membres, mesurée en fonction des distances entre les clusters et à l’intérieur des clusters.
Notons par la lettre δ une mesure de la distance inter-cluster et par Δ une mesure de la distance intra-cluster (qui est aussi appelée diamètre du cluster). L’indice GDI, relatif à ces distances, est défini ainsi :
![]()
Avec k et k’ entre 1 et K.
Six définitions différentes de δ (notées δ1 à δ6) et trois définitions de Δ (notées Δ1 à Δ3) ont été suggérées. Cela conduit à 18 indices différents notés Cuv : ici u est un entier désignant la distance entre les clusters (1 ≤ u ≤ 6) et v un entier désignant la distance au sein des groupes (1 ≤ v ≤ 3). Les définitions des distances Δ au sein du cluster sont :
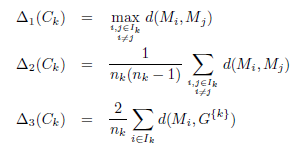
Ici d est la distance euclidienne. Le facteur 2 dans la définition de Δ3 permet d’interpréter la valeur comme un diamètre plutôt que comme un rayon. Les définitions des distances entre clusters δ sont :
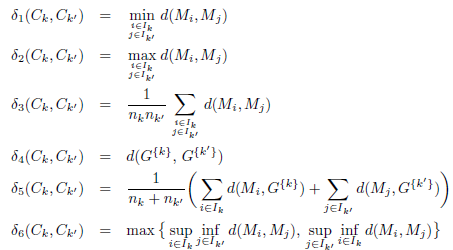
Les quatre premières distances (δ1 à δ4) apparaissent dans les algorithmes de clustering ascendant et sont respectivement appelées liaison simple, liaison complète, liaison moyenne et liaison centroïde. La mesure δ5 est la moyenne pondérée (avec les poids nk et nk′ ) des distances moyennes entre les points des clusters Ck et Ck′ et leur barycentre respectif. La mesure δ6 est la distance de Hausdorff DH.
Baker-Hubert Gamma
L’indice Gamma de Baker-Hubert est une adaptation, dans le cadre du clustering, de l’indice Γ de corrélation entre deux vecteurs de données A et B de même taille.
Généralement, pour deux indices i et j tels que ai < aj , on dit que les deux vecteurs sont concordants si bi < bj , autrement dit si les valeurs se classent dans le même ordre dans les deux vecteurs. On calcule le nombre s+ de couples concordants {i, j} et le nombre s− de couples discordants. Notez que les inégalités sont strictes, ce qui signifie que les égalités sont supprimées. Dans ce contexte, l’indice Γ est classiquement défini ainsi :
![]()
La valeur est entre -1et 1.
Dans le cadre d’une partition, le premier vecteur A est choisi pour être l’ensemble des distances dij entre couples de points {Mi,Mj} (avec i < j). Le deuxième vecteur B est un vecteur binaire : dans ce vecteur, la coordonnée correspondant à un couple {Mi,Mj} vaut 0 si les deux points sont dans le même cluster et 1 sinon. Ces deux vecteurs ont une longueur NT = N(N − 1)/2.
Le nombre s+ représente le nombre de fois qu’une distance entre deux points appartenant à un même cluster (c’est-à-dire un couple pour lequel la valeur du vecteur B est 0) est strictement inférieure à la distance entre deux points n’appartenant pas au même cluster. cluster (c’est-à-dire un couple pour lequel la valeur du vecteur B est 1).
Le nombre s− représente le nombre de fois où la situation inverse se produit, c’est-à-dire qu’une distance entre deux points appartenant à un même cluster (valeur 0 dans B) est strictement supérieure à une distance entre deux points n’appartenant pas au même cluster. (valeur 1 en B). Les cas où il y a égalité (égalité ou ex-aequos) ne sont pas pris en compte.
Il existe des distances inter-clusters NB et, pour chacune d’entre elles, on compare avec les distances intra-clusters NW : on effectue finalement des comparaisons NB × NW. On peut écrire les nombres s+ et s− sous la forme suivante :
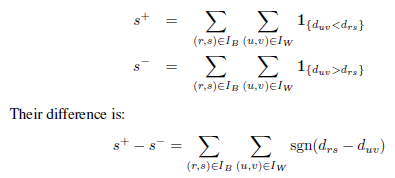
G+
En utilisant les mêmes notations que pour l’indice Γ de Baker-Hubert, l’indice G+ est défini ainsi :
![]()
C’est la proportion de couples discordants parmi tous les couples de points distincts.
Ksq_DetW
Comme son nom l’indique, sa formule est K²|WG|.
Log_Det_Ratio
L’index Log_Det_Ratio est défini comme ceci :
![]()
où T est la matrice de diffusion et WG. Il s’agit d’une variante logarithmique de l’indice Det_Ratio.
Log_SS_Ratio
L’index Log_SS_Ratio est défini comme ceci :
![]()
où BGSS et WGSS sont respectivement les traces des matrices BG et WG.
McClain-Rao
Quant à l’indice C, notons SW la somme des distances intra-cluster :
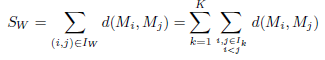
Rappelons que le nombre total de distances entre des paires de points appartenant à un même cluster est NW. Notons SB la somme des distances entre clusters :
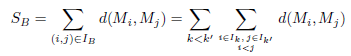
Le nombre total de distances entre des paires de points qui n’appartiennent pas au même cluster est NB = N(N − 1)/2 − NW. L’indice de McClain-Rao est défini comme le quotient entre les distances moyennes au sein d’une cluster et entre les clusters :
![]()
PBM
L’indice PBM (acronyme constitué des initiales des noms de ses auteurs, Pakhira, Bandyopadhyay et Maulik) est calculé à partir des distances entre les points et leurs barycentres et des distances entre les barycentres eux-mêmes.
Notons par DB la plus grande distance entre deux barycentres de cluster :
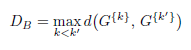
En revanche, notons EW la somme des distances des points de chaque cluster à leur barycentre et ET la somme des distances de tous les points au barycentre G de l’ensemble des données :
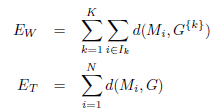
L’index PBM est défini comme ceci :
![]()
ET est une constante qui ne dépend ni de la partition, ni du nombre de clusters.
Point-Bisérial
De manière générale, en statistique, le coefficient point-bisérial est une mesure de corrélation entre une variable continue A et une variable binaire B (c’est-à-dire une variable dont les valeurs sont 0 ou 1). A et B sont des ensembles de même longueur n.
Les valeurs de A sont réparties en deux groupes A0 et A1 selon que la valeur correspondante dans B est 0 ou 1. Notons MA0 et MA1 les moyennes dans A0 et A1, et nA0 et nA1 le nombre d’éléments dans chaque groupe. Le coefficient de corrélation point-bisérial est défini comme la quantité :
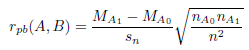
où sn est l’écart type de A.
Dans le cadre d’une comparaison entre différents clusterings, le terme sn peut être omis car il ne dépend pas des partitions mais uniquement de l’ensemble des données.
Comme dans le cas de l’indice Γ, on adapte cette définition en choisissant A comme l’ensemble des NT distances entre couples de points Mi et Mj. La valeur correspondante dans B est 1 si les deux points se trouvent dans le même cluster et 0 sinon :
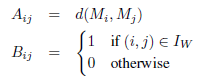
MA1 est la moyenne de toutes les distances au sein du cluster et MA0 est la moyenne de toutes les distances entre les clusters. Ainsi, la définition de l’indice point-bisérial est :
![]()
Ratkowsky-Lance
On calcule la moyenne ¯R des quotients entre BGSS et TSS pour chaque dimension de la donnée, c’est-à-dire pour chaque colonne de la matrice A. Notons :
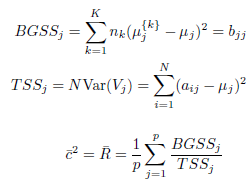
BGSSj est en fait le j-ème terme diagonal de la matrice BG. L’indice de Ratkowsky-Lance (¯c/√K) est défini comme ceci :
![]()
Ray-Turi
L’indice de Ray-Turi est défini comme un quotient :
– le numérateur est la moyenne des carrés des distances de tous les points par rapport au barycentre du cluster auquel ils appartiennent :
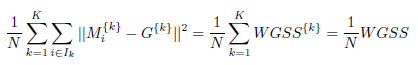
– le dénominateur est le minimum des carrés des distances Δkk′ entre tous les barycentres du cluster :
![]()
L’indice de Ray-Turi peut donc s’écrire ainsi :
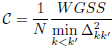
Scott-Symons
Cet indice est la somme pondérée des logarithmes des déterminants de la matrice de variance-covariance de chaque cluster. Cela peut s’écrire ainsi :
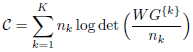
Les déterminants des matrices WG{k} sont supérieurs ou égaux à 0 car ces matrices sont semi-définies positives. Si l’un d’eux est égal à 0, l’index est indéfini.
SD_Scat et SD_Dis
On définit deux grandeurs S et D appelées respectivement diffusion moyenne des clusters et séparation totale entre clusters.
La diffusion moyenne des clusters, notée S, est définie comme suit. Considérons le vecteur de variances pour chaque variable de l’ensemble de données. C’est un vecteur V de taille p défini par :
![]()
De même, on définit des vecteurs de variance V{k} pour chaque cluster Ck :
![]()
La quantité S est la moyenne des normes des vecteurs V{k} divisée par la norme du vecteur V :
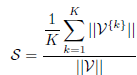
En revanche, la séparation totale entre clusters, notée D, est définie comme suit. Notons Dmax et Dmin respectivement la plus grande et la plus petite distance entre les barycentres des clusters :
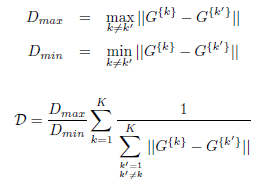
L’index SD est finalement défini comme ceci :
![]()
où α est un poids égal à la valeur de D obtenue pour la partition comportant le plus grand nombre de clusters. Afin de comparer plusieurs partitions des données, il faut d’abord calculer la valeur de D correspondant au plus grand nombre de clusters afin de retrouver la valeur du coefficient α puis calculer les autres indices à partir de ce coefficient.
S_Dbw
Cet indice s’appuie sur la notion de densité de points appartenant à deux clusters. On définit d’abord une valeur limite σ égale à la racine carrée de la somme des normes des vecteurs de variance V{k} divisée par le nombre de clusters :
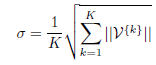
La densité γkk′ pour un point donné, relative à deux clusters Ck et Ck′ , est égale au nombre de points dans ces deux clusters dont la distance à ce point est inférieure à σ. Géométriquement, cela revient à considérer la boule de rayon σ centrée en un point donné et à compter le nombre de points de Ck ∪ Ck′ situés dans cette boule.
Pour chaque paire de clusters, évaluons les densités pour les barycentres G{k} et G{k′} des clusters et pour leur milieu Hkk′ . On forme le quotient Rkk’ entre la densité au milieu et la plus grande densité aux deux barycentres :
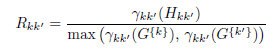
En revanche, on définit une densité inter-clusters G comme la moyenne des quotients Rkk′ :
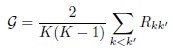
L’indice S-Dbw est défini comme la somme de la dispersion moyenne dans les clusters S et de la densité inter-clusters G :
![]()
Silhouette
Valide les performances en fonction des distances intra et inter-cluster:
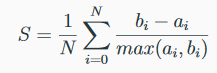
avec a(i) la dissimilarité moyenne avec les autres données du cluster et b(i) la dissimilarité la plus faible avec tout cluster non membre pour chaque x_i et centre du cluster y:

Le coefficient de silhouette varie entre -1 (pire classement) et 1 (meilleur classement). La moyenne globale de Silhouette est souvent calculée.

Tau
Utilisant les mêmes notations que pour l’indice Gamma, l’indice τ de Kendall entre deux vecteurs de données de longueur NT est classiquement défini en statistique comme la quantité :
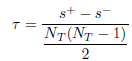
Les nombres s+ et s− ne comptent pas les liens, donc si une distance entre clusters et une distance intra-cluster sont égales, elles n’entrent pas dans le numérateur. Afin de prendre en compte les égalités, on modifie le dénominateur et définit l’indice corrigé τc comme ceci :
![]()
avec
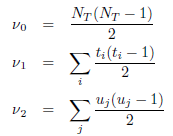
où ti est le nombre de valeurs dans le i-ème groupe de liens pour le vecteur A et uj est le nombre de valeurs dans le j-ème groupe de liens pour le vecteur B. Ici le vecteur B est constitué uniquement de valeurs 0 et 1 (correspondant respectivement aux paires inter-cluster et intra-cluster) et on a ainsi :
![]()
Un calcul simple montre que ν0 − ν2 = NBNW. Si l’on fait l’hypothèse raisonnable que le vecteur A contient peu de valeurs identiques, on peut estimer que ν2 est négligeable par rapport à ν0. Ceci justifie la définition suivante de l’indice de clustering Tau :
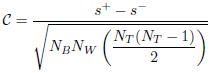
Trace_W
L’index Trace_W est défini comme ceci :
![]()
Trace_WiB
L’index Trace_WiB est défini comme ceci :
![]()
Wemmert-Gançarski
L’indice de Wemmert-Gançarski est construit à partir des quotients de distances entre les points et les barycentres de tous les clusters.
Pour un point M appartenant au cluster Ck, on forme le quotient R(M) entre la distance de ce point au barycentre du cluster auquel il appartient et la plus petite distance de ce point aux barycentres de tous les autres clusters :
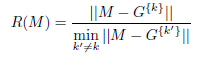
On fait ensuite la moyenne de ces quotients dans chaque cluster. Si cette moyenne est supérieure à 1, on l’ignore, sinon on prend son complément à 1. Précisément, définissons :
![]()
L’indice de Wemmert-Gançarski est défini comme la moyenne pondérée, pour tous les clusters, des quantités Jk comme ceci :
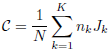
Ce qui peut se réécrire comme :
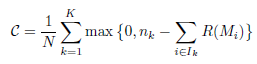
Xie-Beni
L’indice de Xie-Beni est un indice de clustering flou, mais il s’applique également au clustering net.
Elle est définie comme le quotient entre l’erreur quadratique moyenne et le minimum des distances carrées minimales entre les points des clusters. L’erreur quadratique moyenne, dans le cas d’un clustering net, est simplement la quantité 1/N*WGSS, autrement dit la moyenne des carrés des distances de tous les points par rapport au barycentre du cluster auquel ils appartiennent.
![]()
et l’indice Xie-Beni peut s’écrire ainsi :