Contenus
ToggleQualité sur le nombre de clusters
Un sujet lié à la validation des clusters est de décider si le nombre de clusters obtenu est le bon (Qualité sur le nombre de clusters). Ce point est particulièrement important pour les algorithmes qui ont besoin de cette valeur comme paramètre. La procédure habituelle consiste à comparer les caractéristiques des regroupements de différentes tailles. Généralement, des indices de critères internes sont utilisés dans cette comparaison. Un graphique de ces indices pour différents nombres de clusters peut montrer le nombre de grappes le plus probable.
Certains des indices de validité internes peuvent être utilisés à cette fin: indice de Calinsky Harabasz, indice de Silhouette. En utilisant la matrice de dispersion intra-classe (S_W), d’autres critères peuvent être définis (indice de Hartigan et indice de Krzanowski Lai) :

Évaluons le nombre de clusters en comparant un cluster avec la distribution attendue des données étant donné l’hypothèse nulle (pas de clusters). Calculons différents regroupements de données augmentant le nombre de clusters et les comparons aux clusters de données (B) générés avec une distribution uniforme.
La matrice de distance interclasse S_W est calculée pour les deux et comparée. Le nombre correct de clusters est celui où l’écart le plus large apparaît entre le S_W des données et les données uniformes (premier terme de l’équation suivante) :
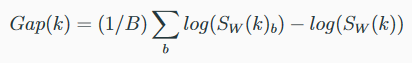
Le nombre probable de clusters est le plus petit nombre qui vérifie :
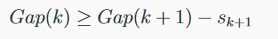
où s_k est défini comme (sd_k est l’écart type du premier terme de Gap) :