Contenus
ToggleAlgorithme de Floyd Warshall
Nous voulons déterminer les chemins les plus courts entre toutes les paires de sommets. Nous pourrions utiliser Dijkstra de Bellman-Ford, avec chaque sommet comme source. Pouvons-nous faire mieux? Dans l’algorithme de Floyd Warshall, nous supposons que nous avons accès à un graphe avec n sommets comme matrice d’adjacence n².
L’algorithme de Floyd Warshall prend en entrée un graphe orienté et valué, décrit par une matrice d’adjacence donnant le poids d’un arc lorsqu’il existe et la valeur ∞ sinon. Le poids d’un chemin entre deux sommets est la somme des poids sur les arcs constituant ce chemin. Les arcs du graphe peuvent avoir des poids négatifs, mais le graphe ne doit pas posséder de circuit de poids strictement négatif. L’algorithme calcule, pour chaque paire de sommets, le poids minimal parmi tous les chemins entre ces deux sommets.
Conditions.
- Cas général étendu
On suppose que les sommets de G sont {1, 2, 3, 4, …, n}. Il résout successivement les sous-problèmes suivants :
Wkij est le poids minimal d’un chemin du sommet i au sommet j n’empruntant que des sommets intermédiaires dans {1, 2, 3, …, k} s’il en existe un, et ∞ sinon. On note Wk la matrice des Wkij.
Pour k = 0, W0 est la matrice d’adjacence définissant le graphe.
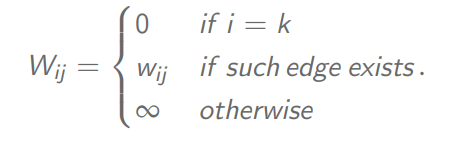
Pour trouver une relation de récurrence, on considère un chemin p entre i et j de poids minimal dont les sommets intermédiaires sont dans {1, 2, 3, …, k} :
- soit p n’emprunte pas le sommet k
- soit p emprunte exactement une fois le sommet k et p est donc la concaténation de deux chemins, entre i et k et k et j respectivement, dont les sommets intermédiaires sont dans {1, 2, 3, …, k-1}.
Soit p un chemin le plus court de i à j avec tous les sommets intermédiaires de l’ensemble {1,. . . , k}. Si k n’est pas un sommet intermédiaire de p, alors p est aussi un chemin le plus court avec tous les sommets intermédiaires de l’ensemble {1,. . . , k – 1}. Si k est un sommet intermédiaire de p, nous décomposons p en un chemin p1 entre i et k, et un chemin p2 entre k et j; ce sont les chemins les plus courts.
L’observation ci-dessus donne la relation de récurrence :
Wkij=min( Wk-1ij, Wk-1ik + Wk-1kj ), pour tous i, j et k dans {1, 2, 3, 4…, n}.
Ainsi on résout les sous-problèmes par valeur de k croissante.
Ce qui donne sur les deux premières étapes :
Exemple de l’algorithme de Floyd Warshall
La première matrice est la matrice d’adjacente puis des plus courts chemins. La deuxième matrice présente les prédécesseurs. Elle est initialisée par une valeur z qui est égale au nombre de la ligne si une valeur existe dans la matrice d’adjacence (à l’état initial). La matrice des prédécesseurs est mise à jour chaque fois qu’une valeur en (i, j) est modifiée. La valeur correspondante en (i, j) de la matrice des prédécesseurs est égale au nombre d’itérations (c’est-à-dire la valeur de la puissance de la matrice).
Optimalité de l’algorithme de Floyd Warshall
Au départ, nous avons les plus courts chemins de taille 1 en partant de tous les sommets. Ensuite, nous calculons les chemins de taille supérieure passant par le sommet 1, et nous ne gardons que les plus courts chemins. La nouvelle itération affiche donc les plus courts chemins de taille 1 et ceux de taille 2 passant par le sommet 1. Par récurrence, nous en déduisons que la dernière matrice affiche les plus courts chemins de taille inférieure au nombre de sommet entre tout couple de sommet.
CODE W est la matrice d'adjacence
pour k de 1 à n
pour i de 1 à n
pour j de 1 à n
Wkij=min( Wk-1ij, Wk-1ik + Wk-1kj )
fin
fin
fin
retourner W