Contenus
ToggleLangages réguliers et expressions régulières
Il existe deux types d’expressions régulières.
On rappelle qu’une grammaire G1 = (T, N, S, R) est une expression régulière à droite si les règles de R sont de la forme : A → aB ou A → a avec A, B ∈ N et a ∈ T.
On rappelle qu’une grammaire G2 = (T, N, S, R) est une expression régulière à gauche si les règles de R sont de la forme : A → Ba ou A → a avec A, B ∈ N et a ∈ T.
L’intérêt de distinguer grammaires régulières à droite ou à gauche apparaît lors de l’analyse : si on lit les symboles du mot à analyser de la gauche vers la droite, alors
- une grammaire régulière à droite sera utilisée pour une analyse descendante, de l’axiome vers le mot
- une grammaire régulière à gauche sera utilisée pour une analyse ascendante, du mot vers l’axiome.
Par exemple, pour analyser le mot aaabb avec la grammaire G1, on construira la dérivation S1 ⇒ aS1 ⇒ aaS1 ⇒ aaaU1 ⇒ aaabU1 ⇒ aaabb; tandis que pour analyser ce mot avec la grammaire G2, on construira la dérivation aaabb ⇐ U2aabb ⇐ U2abb ⇐ U2bb ⇐ S2b ⇐ S2.
Langage et expression
Une expression E est une expression régulière sur un alphabet A si et seulement si :
- E = ∅ ou
- E = ε ou
- E = a avec a ∈ A ou
- E = E1 | E2 et E1 et E2 sont deux expressions régulières sur A ou
- E = E1.E2 et E1 et E2 sont deux expressions régulières sur A ou
- E = E∗1 et E1 est une expression régulière sur A
Les opérateurs ∗, . et | ont une priorité décroissante. Si nécessaire, on peut ajouter des parenthèses.
Le langage L(E) décrit par une expression régulière E définie sur un alphabet A est défini par
- L(E) = ∅ si E = ∅,
- L(E) = {ε} si E = ε,
- L(E) = {a} si E = a,
- L(E) = L(E1) ∪ L(E2) si E = E1 | E2,
- L(E) = L(E1).L(E2) si E = E1.E2,
- L(E) = L(E1)∗ si E = E∗1 et E1 est une expression régulière sur A.
L’équivalence entre expressions régulières et langages réguliers est établie par les deux implications suivantes :
- Toute expression régulière décrit un langage régulier.
- Tout langage régulier peut être décrit par une expression régulière.
Liste d’équivalence triviale :
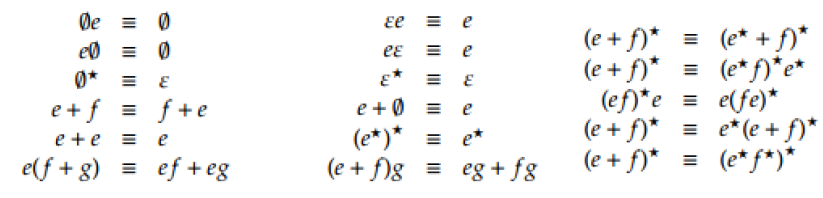
Processus de création d’automate à partir d’une expression régulière

