Programme dual

Programme dual

Bien que le programme primal offre une solution par la méthode du simplexe, nous n’avons que la garantie de ne pas pouvoir améliorer la solution. Afin de prouver qu’il s’agit d’une solution optimale, nous devons aussi résoudre son programme dual. Ce programme dual, en plus de garantir ou non l’optimalité, permettra aussi d’analyser la sensibilité des variables au changement.

Lorsque le programme primal a plus de variables que de contraintes, alors il n’y a pas de garanti de solution (comme pour un système d’équations). Dans ce cas, il est préférable de passer par le dual afin de chercher une solution.

Construction du programme dual

Le programme dual est une symétrie du programme primal : Il y a une contrainte pour chaque variable du programme primal; et une variable duale pour chaque contrainte du programme primal; les coefficients de la fonction objectif primale sont des éléments b du dual et réciproquement. Il est à noter que le dual du dual est le primal.

Pour les règles de transformation particulières suivante, on considère que le primal est sous la forme canonique :

• Si la variable i du primal est positive ou nulle, alors la contrainte i du dual est sous sa forme canonique
• Si la variable i du primal est un nombre réel, alors la contrainte i du dual est une égalité (logique si on considère l’égalité comme une combinaison « inférieur ou égale » et « supérieur ou égale »)
• Si la contrainte j du primal est sous forme canonique, alors la variable j du dual est positive ou nulle
• Si la contrainte j du primal est une égalité, alors la variable j du dual est un nombre réel (logique si on considère l’égalité comme une combinaison « inférieur ou égale » et « supérieur ou égale »)

Compte tenu de la transformation d’un programme linéaire sous forme canonique, le deuxième point et le quatrième point sont normalement non appliqué lors de la transformation en dual pour le calcul du Simplexe !

Voici un résumé de la transformation en Dual par la forme canonique.

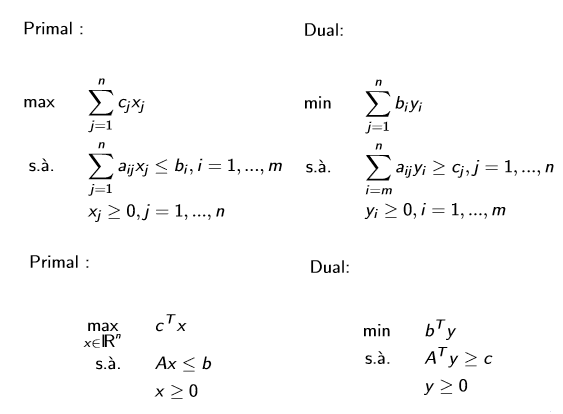
Dualité faible et dualité forte

Dualité faible : pour toute solution du dual et pour toute solution du primal, la valeur objectif du dual z=cx* est supérieur ou égal à celui du primal w=by*.

Dualité forte : si le primal a une solution optimale x* alors le dual a une solution optimale y* et la valeur objectif du primal est égal à celle du dual.

Puisque le dual du dual est le primal, le primal a une solution optimale si et seulement si le dual a une solution optimale.

Il existe une relation dans les solutions du primal et du dual :

• si un problème a des solutions réalisables et un domaine borné pour la fonction objectif, alors il en est de même pour son dual.
• si un problème a des solutions réalisables et un domaine non borné pour la fonction objectif, alors son dual n’a pas de solution réalisable.
• si un problème n’a pas de solutions réalisables, le dual a soit un domaine non borné pour la fonction objectif, soit n’a pas de solutions réalisables.

Interprétation du programme dual