- Graphes parfaits
- Amalgamation de graphes
- Graphe régulier
- Cage
- Graphe biparti
- Graphe de Cayley
- Clique
- Graphe complémentaire
- Graphe de Bruijin
- Densité des graphes (Graphes denses et Graphes creux)
- Graphe d’intervalles
- Graphe en cercle
- Graphe line
- Graphe de Petersen
- Graphe planaire
- Graphe aléatoire
- Graphe à invariance d’échelle
- Graphe cordal ou splité
- Treillis
Contenus
ToggleThéorie des graphes
En théorie des graphes, un graphe G est défini par un couple (S,A) avec S un ensemble fini de sommets, et A un ensemble fini de couple de sommets (si, sj) dans S².
Dans un graphe orienté, les couples (si,sj) de A sont orientés, c’est-à-dire que si est le sommet initial et sj le sommet terminal. Graphiquement, ce couple est un arc du sommet si vers le sommet sj.

Dans un graphe non orienté, les couples (si,sj) ne sont pas orientés. Ainsi, (si,sj) est équivalent à écrire (sj,si). Graphiquement, ce couple est une arête entre les sommets si et sj.
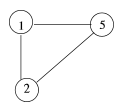
Éléments de terminologie :
- L’ordre d’un graphe est le nombre de ses sommets |S|.
- Une boucle est un arc ou une arête (si,si).
- Un graphe non orienté est dit simple s’il ne contient pas de boucle et s’il comporte au plus une arête entre tout couple de sommets. Sinon il s’agit d’un multi-graphe.
- Un graphe orienté est dit élémentaire s’il ne contient pas de boucle.
- Un graphe orienté est un p-graphe sil comporte au plus p arcs entre tout couple de sommets.
- Un graphe partiel d’un graphe est le graphe obtenu en supprimant certains arcs (ou arêtes).
- Un sous-graphe d’un graphe est le graphe obtenu en supprimant certains sommets et tous les arcs incidents aux sommets supprimés.
- Un graphe est dit complet s’il possède une arête (si,sj) pour tout couple de sommets (ou deux arcs (si,sj) et (sj,si)). Un graphe simple complet à n sommets aura n(n-1)/2 arêtes.
- Un attribut peut être associé à (si,sj). L’attribut peut être une lettre, un mot ou un poids (valeur numérique). Un graphe avec des poids est appelé Réseau.
Considérons un graphe G = (V, E,w) avec une fonction de poids :

Notions d’adjacence :
- Dans un graphe non orienté, un sommet si est dit adjacent à un sommet sj s’il existe une arête entre si et sj. L’ensemble des sommets adjacents à un sommet si est définit par :

- Dans un graphe orienté, on distingue les sommets successeurs (terminaux d’un arc) et prédécesseurs (initiaux d’un arc) :
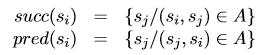
Notions de degré d’un sommet :
- Dans un graphe non orienté, le degré d’un sommet est le nombre d’arêtes incidentes à ce sommet. Dans le cas d’un graphe simple nous avons :
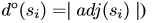
- Dans un graphe orienté, le demi-degré extérieur d’un sommet est le nombre d’arcs partant de ce sommet. Dans un 1-graphe nous avons :

- Dans un graphe orienté, le demi-degré intérieur d’un sommet est le nombre d’arcs arrivant de ce sommet. Dans un 1-graphe nous avons :
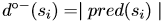
- Le nombre de sommets de degré impair est pair. La somme de tous les degrés est égale à deux fois le nombre d’arêtes. Puisque la somme des degrés est paire et que la somme des degrés des sommets à degré pair est paire, la somme des degrés des sommets à degré impair doit être paire. Si la somme des degrés de sommets avec degré impair est pair, il doit y avoir un nombre pair de ces sommets.
Représentation informatique
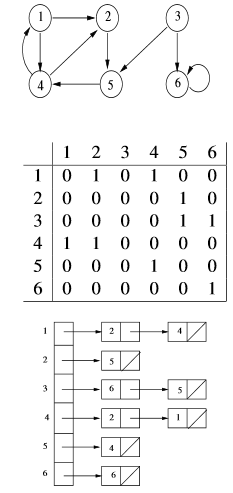
Il existe deux manières « académiques » de représenter un graphe de façon informatique : soit par une matrice d’adjacence, soit par des listes d’adjacence.
On suppose que les sommets de S sont numérotés de 1 à n. La matrice d’adjacence est une matrice M de taille n*n telle que M[i,j] = value si (i,j) dans A, M[i,j] = no value sinon. Dans le cadre de la présence de lien entre le sommet i et j, value = 1 et no value = 0. Dans le cadre de lien valué entre le sommet i et j, value = pondération et no value = infini. Dans un cadre non-orienté, la matrice sera symétrique du triangle supérieur droit. Ce type de codage demande O(|S|²) emplacements mémoire.
La représentation par listes d’adjacences consiste en un tableau T de n listes, une pour chaque sommet de S. Une liste chainée T[si] contient tous les éléments sj de S tels qu’il existe un lien (si, sj) dans A. C’est-à-dire la liste des successeurs de si. Si le graphe est valué, chaque maillon peut contenir des informations sur la pondération. Ce type de codage demande O(|S|+|A|) emplacements mémoire.
Chaque méthode a des avantages comme des inconvénients en fonction des opérations que l’on souhaite effectuer sur le graphe.
Cheminements
Cela peut se calculer par fermeture transitive. Cette dernière est la somme des n premières puissances de la matrice d’adjacence, n=|A|. Le graphe est fortement connexe si toute la matrice comporte value. Une composante fortement connexe est un sous-graphe fortement connexe.
Les mêmes notions existent pour les graphes non orientés sous le nom de chaine et de cycle. Le graphe est dit connexe et l’on parle de composante connexe.
