- Graphe non-dirigé
- Graphe dirigé avec poids non négatifs
- Graphe dirigé avec tous types de poids
- Basé sur une heuristique
- Algorithme A*
- Anytime Repairing A* (ARA*)
- Anytime Dynamic A*
- D*
- Fringe
- Fringe Saving A* (FSA*)
- Generalized Adaptive A* (GAA*)
- Incremental heuristic search
- Informational search
- Iterative deepening A* (IDA*)
- Jump point search
- Lifelong Planning A* (LPA*)
- Multiplier-accelerated A* (MAA*)
- New Bidirectional A* (NBA*)
- Simplified Memory bounded A* (SMA*)
- Realtime A*
- Time-Bounded A* (TBA*)
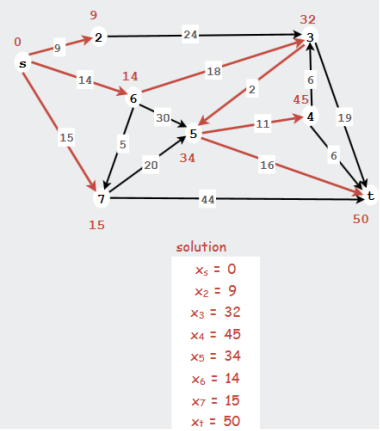
- Résolution du plus court chemin avec Excel
- Passer d’un multi-sources/puits vers un unique
Contenus
ToggleRecherche de chemin
La recherche de chemins, couramment appelée pathfinding consiste à trouver comment se déplacer dans un environnement entre un point de départ et un point d’arrivée en prenant en compte différentes contraintes.
Définition d’un graphe valué
Un graphe valué est un graphe aux arcs desquels on associe un nombre réel appelé longueur de l’arc.
On notera w(x,y) la longueur de l’arc (x,y) entre les sommets x et y.
Par analogie avec la matrice d’adjacence, on peut représenter un graphe valué par une matrice carrée, dont les coefficients correspondent à la valuation des arcs.
Soit un graphe valué dont on a numéroté les sommets de 1 à n . La matrice de valuation de G est la matrice carrée M =mij,de taille n*n, définie par
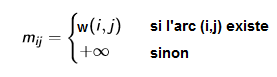
En voici un exemple :

Nous pouvons donc en déduire le programme linéaire suivant, avec xij=1 si l’arc fait partie du plus court chemin, 0 sinon :
- minimize
 avec A l’ensemble des arcs
avec A l’ensemble des arcs - subject to

and for all i, 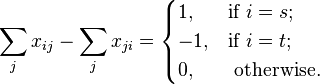

Bien qu’il s’agisse de programmation linéaire, cette méthode peut être très couteuse en mémoire, et même impossible à mettre en place dans certains cas (par exemple s’il s’agit d’un système distribué). Une autre méthode pour connaitre le plus court chemin serait de connaitre le plus petit de tous les chemins d’un sommet vers un autre.
On définit le poids d’un chemin c=(u,…,v)
comme la somme des poids des arcs qui le constituent noté w(c).On définit alors la distance minimum (plus court chemin) entre deux sommets u et v par :
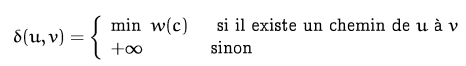
Nous aimerions disposer d’une méthode capable, pour tout graphe et pour toute paire de sommets x et y, de déterminer le plus court chemin entre eux. Pour cela, nous devons comprendre et de caractériser au mieux la structure d’une solution : quelles sont les propriétés d’un plus court chemin ?
Lemme de Koenig. Un plus court chemin entre 2 sommets est élémentaire. Un chemin est élémentaire si chacun des sommets du parcours est visité une seule fois.
Le fait d’énumérer tous les chemins pour déterminer le plus court révèle un grave défaut : son temps d’exécution. Si le nombre de chemins élémentaires est bien fini, il n’en demeure pas moins très grand, de l’ordre de n! sur un graphe d’ordre n.
Problème sous-optimal
Nous avons besoin d’une seconde propriété, fondamentale, la sous-optimalité (voir Programmation Dynamique). Il s’agit de remarquer qu’être un plus court chemin est récursif : une séquence d’un plus court chemin est encore un plus court chemin entre ses extrémités. Ou encore si le trajet le plus rapide entre u et v passe par 2 sommets x et y, ce trajet emprunte nécessairement le plus court chemin entre x et y.
Si p=(u,…,v) est un plus court chemin entre u et v, alors pour tout sommet x sur le chemin p :
- le sous-chemin de p jusqu’à x, (u,…,x), est un plus court chemin de u à x
- le sous-chemin de p depuis x, (x,…,v), est un plus court chemin de x à v
Par l’absurde supposons qu’il existe par exemple entre u et x un chemin q de longueur strictement inférieur à celle de p=(u,…,x,…,v). Alors nous pouvons construire un nouveau chemin p’ entre u et v en substituant q sur (u,…,x) dans le chemin p. La longueur de p’ est alors strictement inférieure à celle de p, ce qui contredit que p est un plus court chemin de u à v.
Arbre de chemins
Il y a un arbre des chemins les plus courts d’un sommet de départ à tous les autres. Supposons que le graphe est connecté, que les arêtes ne sont pas dirigées et que les poids sont non négatifs. Nous développons un nuage de sommets, commençant par s et couvrant finalement tous les sommets. Nous stockons à chaque sommet v une étiquette d (v) représentant la distance de v de s dans le sous-graphe constitué du nuage et de ses sommets adjacents. A chaque étape: nous ajoutons au nuage le sommet en dehors du nuage avec la plus petite étiquette de distance; nous mettons à jour les étiquettes des sommets adjacents à u (voir arbre couvrant).
Considérons une arête e = (u, z) tel que u est le sommet le plus récemment ajouté au nuage et z n’est pas dans le nuage. La relaxation du bord e met à jour la distance d(z) comme suit: d (z) ← min {d(z), d(u) + poids(e)}


