Pathfinding 101

Path search

The path search, commonly called pathfinding consists in finding how to move in an environment between a starting point and an ending point while taking into account various constraints.

Definition of a valued graph

A valued graph is a graph with the arcs of which we associate a real number called the length of the arc.

We denote by w (x, y) the length of the arc (x, y) between the vertices x and y.

By analogy with the adjacency matrix, we can represent a graph valued by a square matrix, the coefficients of which correspond to the valuation of the arcs.

Let be a valued graph whose vertices have been numbered from 1 to n. The valuation matrix of G is the square matrix M = m_ij, of size n * n, defined by

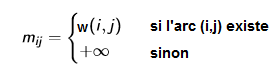
Here is an example:

We can therefore deduce the following linear program, with x_ij= 1 if the arc is part of the shortest path, 0 otherwise:

• minimize with A the set of arcs
• subject to

and for all i,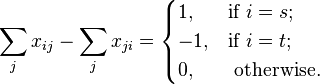

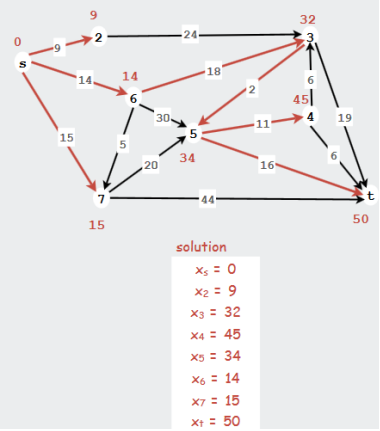
Although it is linear programming, this method can be very expensive in memory, and even impossible to set up in certain cases (for example if it is about a distributed system). Another method of knowing the shortest path would be to know the smallest of all the paths from one vertex to another.

We define the weight of a path c = (u,…, v)

as the sum of the weights of the arcs which constitute it noted w (c).We then define the minimum distance (shortest path) between two vertices u and v by:

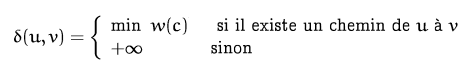
We would like to have a capable method, for any graph and for any pair of vertices x and y, to determine the shortest path between them. For this, we must understand and characterize as well as possible the structure of a solution: what are the properties of a shorter path?

Lemma of Koenig. A shorter path between 2 vertices is elementary. A path is elementary if each of the peaks of the route is visited only once.

Listing all the paths to determine the shortest one reveals a serious flaw: its execution time. If the number of elementary paths is finite, it nonetheless remains very large, of the order of not! on an order graph not.

Suboptimal problem

We need a second, fundamental property, the suboptimality (see Dynamic Programming). It is a matter of noticing that being a shorter path is recursive: a sequence of a shorter path is still a shorter path between its ends. Or if the fastest route between u and v goes through 2 peaks x and y, this route necessarily takes the shortest path between x and y.

Yes p = (u,…, v) is a shorter way between u and v, then for any summit x on the road p :

• the subpath of p up to x, (u,…, x), is a shorter path of u To x
• the subpath of p since x, (x,…, v), is a shorter path of x To v

For the absurd let us suppose that there exists for example between u and x a path q of length strictly less than that of p = (u,…, x,…, v). So we can build a new way p ' Between u and v substituting q on (u,…, x) in the way p. The length of p ' is then strictly lower than that of p, which contradicts that p is a shorter way of u To v.

Tree of paths

There is a tree There is a tree showing the shortest paths from one starting point to all the others. Suppose the graph is connected, the edges are not directed, and the weights are non-negative. We develop a cloud of vertices, starting with s and eventually covering all the vertices. We store at each vertex v a label d (v) representing the distance of v from s in the subgraph made up of the cloud and its adjacent vertices. At each step: we add to the cloud the top outside the cloud with the smallest distance label; we update the labels of the vertices adjacent to u (see spanning tree).

Consider an edge e = (u, z) such that u is the most recently added vertex to the cloud and z is not in the cloud. The relaxation of edge e updates the distance d (z) as follows: d (z) ← min {d (z), d (u) + weight (e)}