Algorithmics 101 - Complex systems and AI

Analysis:

II. Programming paradigms and strategies

Toggle Content

Contenus

Algorithmic

Algorithmics have been around forever, it is a thought process that is described in a logical manner. Although this system seems essential to us today for many sciences, the systematization of algorithmic writing has evolved over time and through technology. It began in the time of the Babylonians, until it was concretely established by René Descartes in the general method proposed by the Discourse on Method in 1637.

Modern algorithms, including a so-called “program” language, made its debut shortly afterwards in 1677. The term we use today, “algorithm”, appears two centuries later.

The algorithm of XX^e and XXI^e century is often based on formalisms like that of Turing machines, which provides a scientific framework for studying the properties of algorithms.

With computer science, algorithms developed a lot in the second half of the XX^e century and Knuth (1969), author of The Art of Computer Programming defines 5 properties which constitute the prerequisites of an algorithm.

1. Finiteness: an algorithm must terminate after a finite number of steps

2. Precise definition: each step of an algorithm must be defined precisely without ambiguity

3. Inputs: quantities that are defined before the algorithm begins

4. Outputs: quantities that have a specified relationship to inputs

5. Performance: all the operations that the algorithm must perform must be sufficiently basic to be able in principle to be carried out in a finite period of time by a man using paper and a pencil.

Markov (1967) defines an algorithm as “An exact prescription defining a processing process which leads from initial data to the final result”.

Which implies the following characteristics:
• Precision of the prescription leaving no room for arbitrariness and universal understanding • Possibility of starting with initial data which can vary within given limits • The orientation of the algorithm in the search for a desired result which must be obtain at the end of the execution from the initial data: this is the conclusion property of the algorithm.

For Minsky (1967) the definition is even more direct:
“A set of rules that tell us, from moment to moment, precisely how to behave”

And finally for Stone (1972)
“An algorithm is a set of rules that precisely defines a sequence of operations such that each rule is effective and defined and the sequence completes in a finite time. »

It further specifies that:
“for those who follow the rules of the algorithm, they must be formulated so that they are followed mechanically without having to think”

For example :
If the instructions require extracting a square root and are performed by someone who knows how to do arithmetic but does not know how to extract a square root, then one must provide a set of rules for extracting a square root, so to satisfy the definition of the algorithm

Many formal or theoretical tools have been developed to describe algorithms, study them, express their qualities, and be able to compare them:

algorithmic structures: control structures and data structures.
the notions of correctness, completeness and termination.
the theory of complexity.

Transcribe an algorithm

THEnatural language : verbose and ambiguous, rarely used for complex algorithms but not prohibited.
Pseudocode : a structured language, but no strict rules defined; Independent of any implementation
Organizational chart : no ambiguity, good readability, writing in the form of standardized symbols
THEprogramming languages : normally intended to transcribe flowcharts into a form understandable by computers; can also be used to describe algorithms
THEalgorithmic languages : language using pseudo-code composed of fixed rules, understandable by a computer, allowing the description and execution of algorithms.

Control structure and data structure

A control structure is a command that controls the order in which the various instructions of an algorithm or a computer program are executed. The processor is responsible for memorizing the address of the next instruction to be executed, the blocks (loops, if, etc.) or the subroutines.

This sequence of instructions is also called the execution flow of a program and it can be represented using a graph of control flow or a automaton. Certain programming paradigm calling on several processors is then exposed to the problem of assignment of tasks in the processors.

A data structure is a logical structure intended to contain data, in order to give them an organization allowing their processing to be simplified. There are many types of data structure depending on the actions to be performed on them, we will not delay any further on this subject.

Each computer language has a type of control structure and data structure. The writing of an algorithm is very often based on widely used languages such as C, java, etc.

Notions of termination, correction, completeness

Termination is the assurance that the algorithm will terminate in a finite time. The proofs of termination usually involve a strictly decreasing positive integer function at each step / iteration of the algorithm.

Given the guarantee that an algorithm will finish, the proof of correctness must provide the assurance that if the algorithm ends by giving a proposed solution, then this solution is correct (in the sense that it answers the problem posed).

The proof of completeness guarantees that, for a given problem space, the algorithm, if it finishes, will give a solution for each of the inputs of the algorithm.

Termination : the algorithm has time complexity.

Correction : any computed answer of the algorithm is solution of the problem.

Completeness : the algorithm can calculate a response for any instance of the problem.

Algorithmic complexity

The complexity of algorithms is an evaluation of the cost of running an algorithm in terms of time (temporal complexity) or memory space (spatial complexity). The efficiency of an algorithm therefore depends on these two criteria, which we will try to minimize.

Algorithmic complexity makes it possible to learn about the intrinsic efficiency of a
algorithm: the “natural” performance of an algorithm outside the environment in which the latter will be implemented.

There are several types of analysis of the performance of an algorithm:

Optimistic analysis (best-case analysis or best-case analysis).
The average analysis is often a factor in the programming paradigm used.
Pessimistic analysis (worst-case analysis or worst-case analysis).

Complexity classes are sets of problems which all have the same complexity according to a certain criterion. The best-known classes are classes defined on Turing machines (deterministic or non-deterministic - see the course on automata) with time and space constraints. There is a relationship between algorithmic complexity and its energy cost of operation, called Landauer's principle.

Here is a list of the most commonly encountered complexities:

Rating	Complexity type
$O (1)$	constant complexity: an assignment, an elementary calculation, etc.
$O (\ log (n))$	logarithmic complexity: dichotomy, tree
$We)$	linear complexity: a loop
$O (n \ log (n))$	quasi-linear complexity: divide and rule, tree
$O (n ^ {2})$	quadratic complexity: nesting two loops
$O (n ^ {3})$	cubic complexity: nesting of three loops
$O (n ^ p)$	polynomial complexity: nesting of loops without knowledge of states
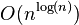$O (n ^ {\ log (n)})$	quasi-polynomial complexity: divide and conquer
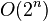$O (2 ^ {n})$	exponential complexity: tree, brute force
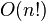$We!)$	factorial complexity: naive approach to combinatorial enumeration