Naive / greedy / enumeration algorithm

Contents

Naive algorithm

a algorithm naif aims to provide a basic result to a problem. The naive method does not make any preparatory calculations and uses only the basic data of the problem.

Take for example a problem of backpack. The naive algorithm would consist in taking first the objects of the smallest size until no more new objects can be put in the bag.

for i of 1 To not
   if w [i] + w_conso ≤ W so
      x [i]: = 1 w_conso: = w_conso + w [i]
   otherwise
      x [i]: = 0
   end if
end for

Greedy algorithm (intuitive method)

Like the naive algorithm, a so-called greedy algorithm is built on a simple principle: during an iteration, the algorithm always makes the decision of the “best choice”. A locally optimal choice is therefore necessary with the objective that this choice will lead to the overall optimal solution. However, the algorithm does not give any guarantee that the latter solution is an optimal solution.

Intuitively, we can say to ourselves that to maximize the utility in the backpack problem, it suffices to put the element having the greatest utility (with a size compatible with the remaining size in the bag) until no more have enough room in the bag.

For this we will consider x and w the vectors of the choice of the object and of its weight sorted in decreasing order of efficiency (efficiency = utility / weight). Then the algorithm works like the naive method.

A simple example makes it possible to understand that this choice is not always optimal: let us take an object of size 1 and utility 2, and an object of size and utility equal to the size of the bag. Under these conditions the first object with the greatest utility, it will be chosen first. There is no more room to place the second object. The optimal solution would be to choose only the second object in the bag.

Brute force or enumeration

Unlike the naive algorithm, this method guarantees the overall optimum, but its execution time and memory consumption can quickly exceed the limits of a PC. The principle is simple, you have to list all the possible solutions to the problem and choose the best solution.

Usually, the solution tree is represented as the name suggests as a tree. Let's take the example of the backpack problem with four objects with the following parameters and a bag size of 30:

object	1	2	3	4
u_i	7	3	4	3
w_i	13	8	12	10

The tree is built by iteration: at each iteration, the new leaves represent whether or not to take the next object. We get the following binary tree:

naive algorithm greedy algorithm brute force enumeration

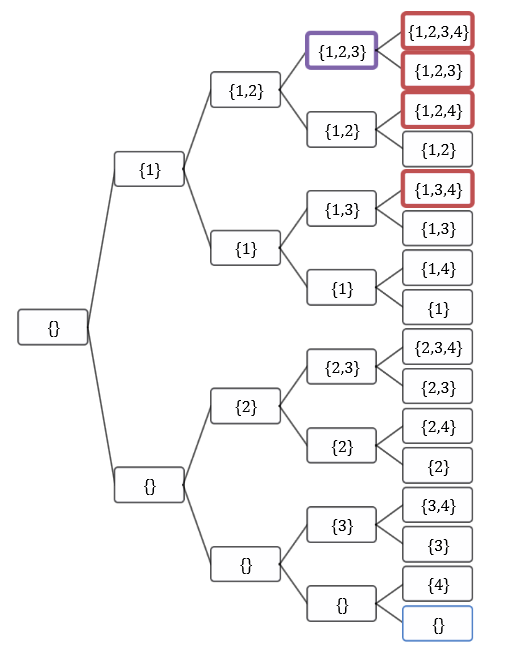
The tops in red exceed the maximum bag size, the top in purple is the optimal solution. As you can see, the number of leaf is equal to 2^(n-1) for the object not. The number of nodes generated up to the object n is therefore 2^not -1.