Contents
ToggleCorrected exercises: recursive algorithm
The following corrected exercises concern the principle of recursive algorithm, for example Fibonacci, the Towers of Hanoi and many other cases math. The exercises include simple recursion, tail recursion, cross-recursion or mutual recursion, and the principle of memoization (for more details on this last point, please see the principle of dynamic programming).

Exercise 1
Rewrite the following algorithms in recursive form in terminal form when possible.



A last one for the road. This time you have to understand what it does before making it terminal recursive!

We consider that n is a positive integer or zero.


algo3 is already recursive but not terminal. Since the algorithm returns 2^not, we will change its structure to make it terminal.

For the last algorithm, we must first understand that it calculates the gcd between a and b. Do a test by hand, you will understand that the first branch is useless, so we will remove it for the recursion. The variable r is not present to replace the value of a and b, so it will not fit in the recursion.

Exercise 2
The Fibonacci problem (1170 – 1250):
“Originally possessing a pair of rabbits, how many pairs do you get in twelve months if each pair generates a new pair every month from the second month of its existence? Rabbits never die.”
So if we take an example of the first 7 months.
Month | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Couple | 1 | 1 | 2 | 3 | 5 | 8 | 13 |
a – Express the population of couples of month n as a function of the previous months.
b – Write an iterative algorithm that calculates the number of couples after 12 months.
c – Modify the iterative algorithm to calculate the number of months after which the population of rabbit pairs exceeds 300.
d – Write the recursive algorithm to calculate the number of pairs of rabbits after n months.
has -
The number of pairs of rabbits in month n is the sum of the pairs existing the month before (in month n − 1) and the new pairs in month n.
However, the text specifies that all the couples existing two months before (at month n − 2) reproduce.
Therefore, at month n ≥ 2 the number of rabbits is equal to the sum of month n-1 and n-2. At month 0 and month 1, there is only one pair.
b-

vs -

d-

It is possible to do Fibonacci in terminal form:

Or by using memorization:

Exercise 3
a – Write an algorithm that calculates the maximum of 2 real numbers
b – Write a recursive algorithm that calculates the maximum of 3 real numbers using the algorithm of a. Show call tree.
c – Write a recursive algorithm that calculates the maximum of 4 real numbers using the algorithm of a. Show call tree.
d – Is the algorithm recursive?
has -

b-

Here, Maximum2 acts as the terminal condition of the recursive algorithm. The call stack is as follows:

vs -

The call stack is as follows:

d – Although it looks like a recursion, it's more of a function overload or function call to reduce the size of the problem. It is not a recursive algorithm per se.
Exercise 4
a – Are the algorithms below recursive algorithms?
b – Are they terminal?
c – Do they end?



has -
The log and sum algorithms are recursive: each contains at least one call to itself, on the other hand, power is not: it calls the algorithm then. It is necessary to replace then by power.
b-
log is terminal, power and sum are not because they require computation during the recursion.
vs -
log terminates for any integer x. The iteration of integer division by 2 leads to 0, and the base case 0 ends with the execution of return.
For the power algorithm (corrected), the base case 0 ends with the execution of returning. If the algorithm terminates for the value n−1 then it also terminates for the value n is executing return. Don't forget that a user can enter anything like power(2, – 5) so you have to check his termination.
sum does not end when n is strictly positive. Indeed, the algorithm for n terminates only if the algorithm terminates for n+1. However, there is no strictly positive integer for which the algorithm stops.
Exercise 5
a – We want to write a recursive function that calculates the square of an integer. To do this, we will have to use a relation between square(n) and square(n-1) knowing that square(1)=1. Represent the call stack for carre(5).
b – Combinations are a mathematical concept describing the different ways of choosing a given number of objects from a set of given size. For example how much it is possible to draw 6 Lotto balls out of 60 in the reel. Or draw 3 cards from a tarot deck. The combination of choosing p elements from n elements is denoted C(p,n)=(n/p)*C(p-1, n-1). We got C(0,n)=1 and C(n,n)=1.
Write the non-terminal recursive function then the terminal recursive function, and show the call stack for C(3,7). Via the terminal function, deduce the iterative function.
c – For combinations, we generally prefer to avoid the b method because the divisions can create rounding problems. We will instead use the following relationship: C(p,n)=C(p,n-1)+C(p-1,n-1). Write the recursive function and the stack or tree calls for C(2,4).
a – To find a link between square(n) and square(n-1), we use the formula: (n+ 1)² = n² + 2n+ 1. We write it as a function of n to n-1: n² = (n−1)²+2(n−1)+1 hence square(n)=square(n-1)+2*n-1. That's it !

The call stack is:

b – Everything is said in the statement, all that remains is to write it down.

Here is the list of calls for C(3,7):

And now for the terminal version, it's a little more complicated because you have to wonder about what you have to keep in memory for the recursion. At each iteration we did n/p times the previous one, so n/p * (n-1)/(p-1). We could have written it n(n-1)/p(p-1). So we could store the multiplication of decreasing n on one side and decreasing p on the other.

Here is the call stack for C(3,7,1,1):

We deduce the iterative function from the terminal function. Just do a Until the stopping condition is reached.

c – We already have the recursive relation in the statement.

Here is the call tree for C(2,4):

Exercise 6
We define the McCarthy function as follows:

What does the function do for n>100? for n=98, 99, 100? In general for n<=100?
We are going to do a bit of math… If n > 100 we will have n-10. The problem arises when we start with n<=100. Calculate for 98, 99 and 100. We will do a direct demonstration.
For n between 90 and 100 inclusive – i.e. 11 consecutive values, this will be useful later. We will do Carthy(Carthy(n+11)) so we will exceed the value of 100. So we will have Carthy(n+1) in the end. If n+1 is still not greater than 100, we put the cover back. So we stop when we go from 100 to 101, or Carthy(101)=101-10=91.
In resumes what we left at the beginning of the previous paragraph. On the last 11 consecutive values, we will have a result of 91. We note that any number between 0 and 89, to which we add 11 as long as it is less than 90 will have a final value between 90 and 100 inclusive.
We deduce that Carthy on a value of 100 or less will give the value of 91.
It needed a bit of math. Computer science is just another syntactic way of doing math!
Exercise 7
We are talking about recursion cross when two functions call each other recursively.
We will test on a cross recursion to know if a number is even (true) or odd (false). Here is the proposal:

Test for even(2), odd(3), even(3), and odd(2). Is the algorithm correct? Otherwise change it to check the correction ← PS: if the teacher asks that, it's because the algo has a problem CQFD
Obviously the algo is not correct. Take even(3) → odd(2) → even(1) → odd(0) → even(-1) → odd(-2) → etc. This is because the stop conditions only work if the number of the even method is even and the odd method is odd. We will only change the odd method.

It's up to you to retest if it's correct now!
To have a more robust algorithm, it would be necessary to check that the input integer is positive (or make the absolute value).
In the case of an entry with a double or floating, it is possible to make it whole by rounding it. To do this, you need to know the number after the decimal point with the following calculation comma=n*10[10]. If comma<5 then we cast (integer)n, otherwise we cast (integer)n+1.
Exercise 8
It is impossible to conclude on the recursive without mentioning the famous Towers of Hanoi (the obsession of students and sometimes also of lecturers and teachers!). So we're going to take it slowly.

There are n trays of different sizes, and 3 rods, numbered from 0 to 2.
Initially, all trays are located on stem i. The goal is to transfer them to the rod j, respecting the following rules:
– You can only move one board at a time.
– The trays must always be arranged in decreasing size on a rod (the largest at the bottom then in decreasing order going up on the rod).
1 – Solve the problem by hand if n = 2, i = 0 and j = 2 (so 2 trays, they are all base on rod 0 and we want to put them on rod 2).
2 – Solve the problem by hand if n = 3, i = 0 and j = 2 (so 3 trays, they are all base on rod 0 and we want to put them on rod 2).
3 – Suppose a friend of yours knows how to solve the problem for some n, and any which i and j. You are asked to solve the problem for n + 1. You have the right to use your friend's help. How do you do it?
4 – Write the recursive function that solves this problem for all n, i, j (If you can do it without cheating, congratulations! Otherwise it's normal, we almost all went through this great moment of misunderstanding and questioning of her career…)
1 –
The small board is transferred from 0 to 1.
The large board is transferred from 0 to 2.
We transfer the small tray from 1 to 2.
2 –
The small board is transferred from 0 to 2.
We transfer the average plateau from 0 to 1.
We transfer the small board from 2 to 1. (we moved 2 boards from 0 to 1).
The large board is transferred from 0 to 2.
The small board is transferred from 1 to 0.
We transfer the medium board from 1 to 2.
We transfer the small board from 0 to 2. (we moved 2 boards from 1 to 2).
3 –
We move n trays from i to the location which is neither i nor j (by the series of three manipulations of point 2). We then move the last board (the biggest) from i to j. We call on the friend to move the n trays to j.
4 –
If you find that… champagne! We will rename for ease the stems in d for the starting one, a for the arrival one and r for the remaining one

Let's look at how it works, here is the general structure of the algorithm:
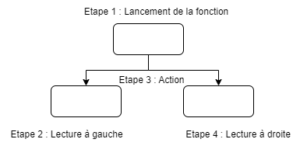
Take for example Hanoi(2,d,a,r), denote the set of recursions with the basic order (d,a,r) even if this does not make sense of a recursive view weight:
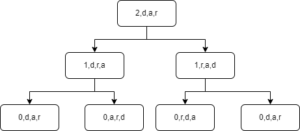
Note that nodes with an n value of 0 are of no use because the function will be empty.
Now let's take the tree with the order of actions. To traverse the tree let's do a tree traversal
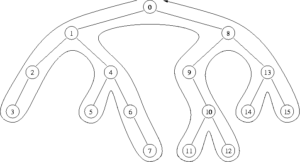
A node carries out its action when we pass under it:
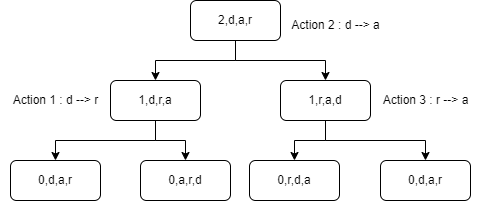
Which would give the following movements:
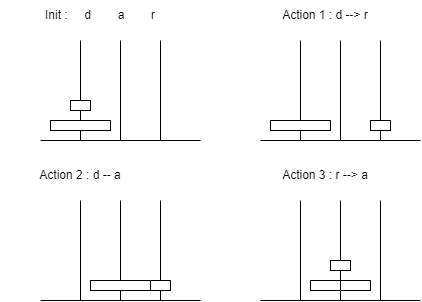
Exercise 9
Write a program to find the GCD of two numbers using recursion.
Here is the idea behind the algorithm:
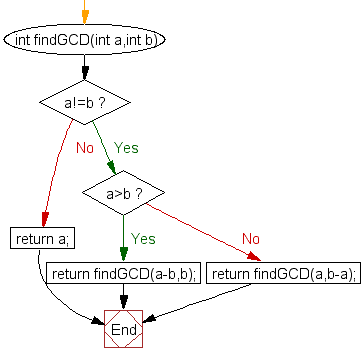
Which gives the following algorithm:

It is also possible to do the modulo directly (rather than ab several times) to do a recursion with the remainder:

Exercise 10
Write a program to convert a decimal number to binary using recursion.
Here is the idea behind the algorithm:
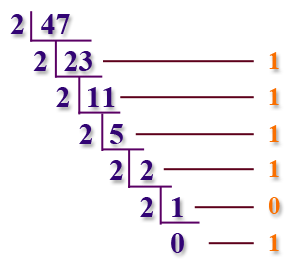

Exercise 11
Write a program to find the LCM of two numbers using recursion.

Here is the algorithm:
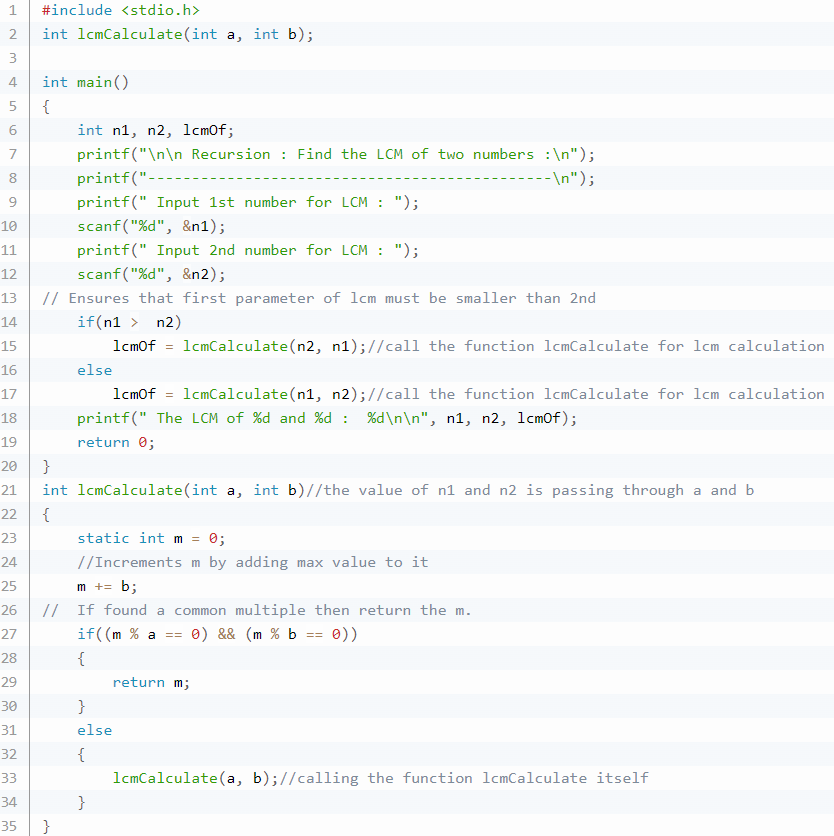
The recursive lcm() function takes two integers as arguments. Take a static variable m and initialize it with zero, then update with one of the numbers. Here we update variable m with b, so variable m will always be divisible by variable b. Therefore, we need to check only with variable a i.e. (m%a == 0).
Since we are adding the largest number to the variable m, then the variable b must contain the largest number. When calling lcm(), we need to pass the smaller number as a and the larger number as b.
If we add the larger number, the number of recursive calls will be the minimum, but if we add the smaller number, the number of recursive calls will be more than the previous case. We know that fewer recursive calls give high performance.
Let's take the example of numbers 3 and 7. If we add the larger number 7 to the sum variable then,
0+7 = 7 (call from the main function), 7%3 != 0
7+7 = 14 (first recursive call), 14%3 != 0
14+7 = 21 (second recursive call)
21 is divisible by 3 and 7
So there will only be 2 recursive calls.
Similarly, if we take the smallest number (3) then,
0+3 = 3 , 3%7 != 0
3+3 = 6 , 6%7 != 0
6+3 = 9 , 9%7 != 0
9+3 = 12 , 12%7 != 0
12+3 = 15 , 15%7 != 0
15+3 = 18 , 18%7 != 0
18+3 = 21
21 is divisible by 3 and 7
There will therefore be 6 recursive calls.
Exercise 12
Write a program to check if a given string is Palindrome or not.
Exercise 13
The number Pi can be calculated by the following formula:
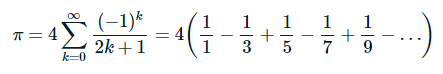
Write a recursive algorithm to calculate the value of Pi by considering the sequence up to rank n.
Do the same with the following approximations of Pi.
Gregory-Leibniz series:

And the older series of Madhava, Ramanujan, David and Chudnovsky (the factorial will be a recursive call in its own right):

Here is the recursive algorithm:
gregory(n)
{
if(n==0) return 4
return 4*pow(-1,n)/(2*n+1)+gregory(n-1)
}
The other formulas follow the same principle, no need to detail everything. Be careful all the same to use the correct calculation in the recursion! (the algorithms will be easier to write in non-terminal recursive.
Exercise 14
In the 1920s, Wilhelm Ackermann and Gabriel Sudan, then students under David Hilbert, studied the foundations of computability. Sudan is the first to give an example of a primitive recursive but non-recursive function, then called Sudan's function. Soon after and independently, in 1928, Ackermann published his own example of a primitive recursive but non-recursive function. Originally, Ackermann considers a function ϕ(m, n, p) dependent on three variables.
A function of only two variables is given later by Rózsa Péter and Raphael Robinson; it is the latter which is known today as the Ackermann function.
The Ackermann-Péter function is defined recursively as follows:

The function grows so fast that it is quickly impossible to write it with a classical number and it is necessary to use Knuth's notation!

The solution is very simple, but I do not recommend running the algorithm on a PC.
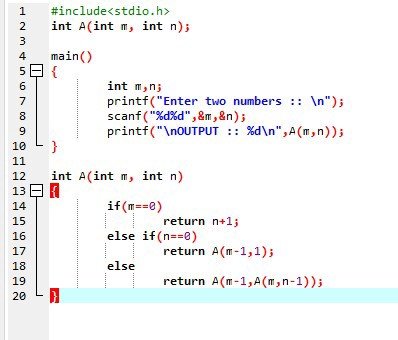
Exercise 15
Here is the function of Sudan, another student of David Hilbert. This function was designed in 1927 so a year earlier than Ackermann's function.
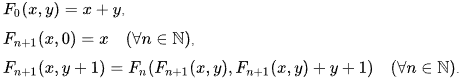
Here, the more the value of n grows, the more the result of the function of the function explodes. Here is the example for F_1(14,14).
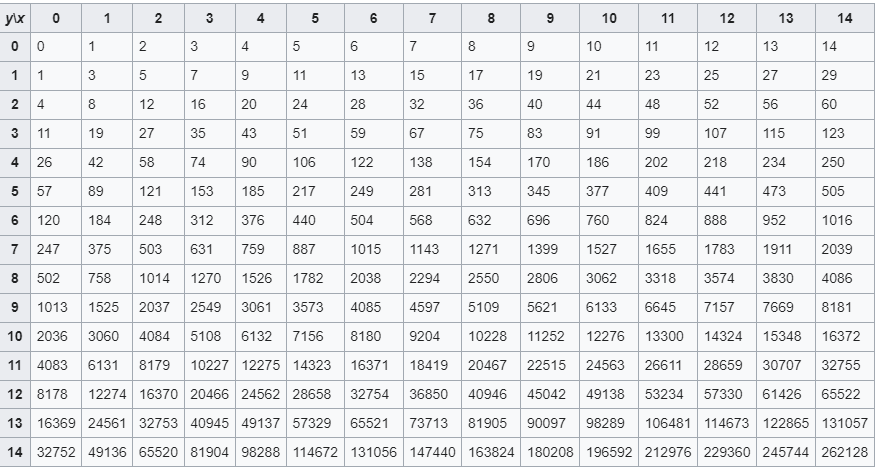
Nothing very complicated, just copy the mathematical formula in the form of recursion.

Exercise 16
Takeuchi's function, abbreviated tak or sometimes tarai, is the recursive presentation of a function named after Ikuo Takeuchi (竹内郁雄). The presentation of the function, which, moreover, admits a fairly simple non-recursive definition, may require very long calculations if the compiler which implements it is not efficient. For this reason, it is often used to test the performance of the implementation of recursive functions by the compiler of a programming language.
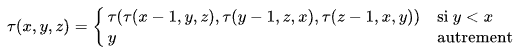
Takeuchi's original definition was:

tarai is the abbreviation of "to pass around" in Japanese. John McCarthy named this function tak() after Takeuchi.
Recursion has been improved thanks to cross-recursion:

Exercise 17
The Male-Female Hofstadter sequence is defined by:
F(0)=1, M(0)=0 and
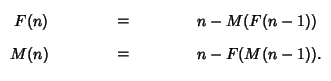
Write a recursive algorithm to calculate the Hofstadter sequence.
Likewise for the sequence G:

This is a cross-recursive (also called perfect) algorithm.

For sequence G, the principle is the same:

Below is an example of a node tree formed when the program is run with values of n between 1 and 21. For example, G(15) will produce the value 9, and G(9) will produce the value 6 , etc. Interestingly, the Fibonacci sequence is visible on the right side of the tree.
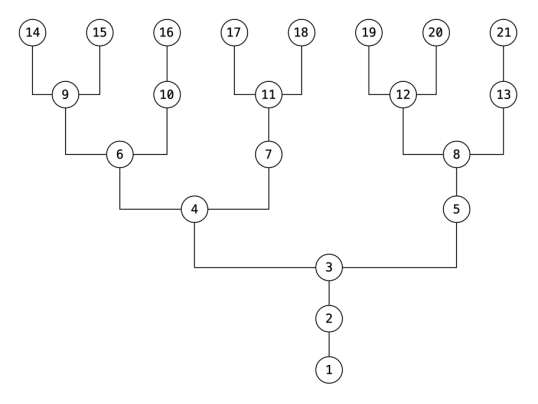
Exercise 18
Some programming languages allow memoization. It is a caching of the return values of a function according to its input values. The purpose of this code optimization technique is to reduce the execution time of a computer program by memorizing the values returned by a function.
Thus, by carrying out the Fibonacci sequence, it is possible to memorize the values already calculated in order to avoid saturating the memory with values already obtained in another branch of the call tree.
In fact, whenever we compute fib(i), we could just cache that result and use it later. So when we call fib(n), we shouldn't have to do much more than 0(n) calls, because there are only O(n) possible values we can cast to fib(n).

Here the recursion tree will be very different from that of the non-terminal variant:
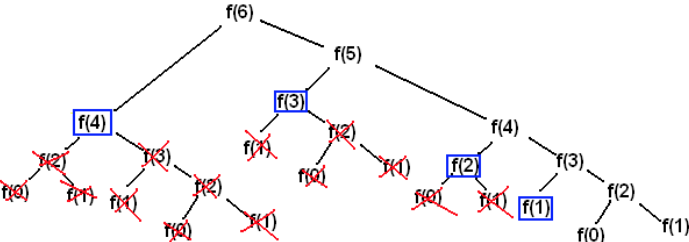
Note that the tree above does not take into account the direction of left call then right call. For greater comfort, it is customary to put the first call as a left son and the second as a right son, therefore the opposite of the tree presented!
Calculation times are greatly reduced as shown in the following diagram on Fibo(100) in its variants:
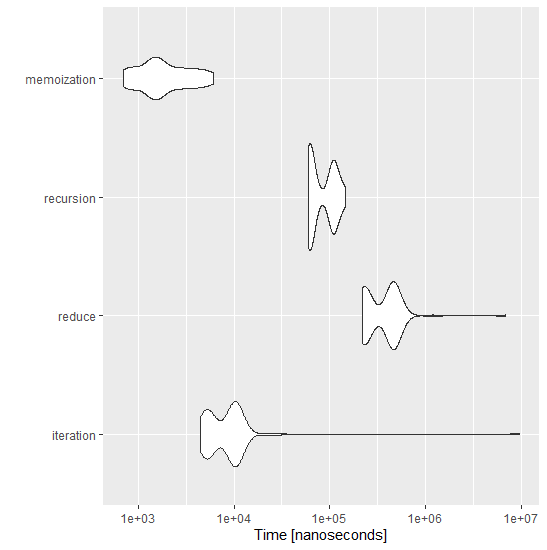
Exercise 19
Some programming languages allow memoization. It is a caching of the return values of a function according to its input values. The purpose of this code optimization technique is to reduce the execution time of a computer program by memorizing the values returned by a function.
Write an algorithm calculating factorial n (n!) using the principle of memoization.
Here is the classic solution for doing recursive factorial calculation:

The non-memorized implementation above, given the nature of the recursive algorithm involved, would require n + 1 invocations of factorials to arrive at a result, and each of these invocations, in turn, has an associated cost in terms of time required for the function. to return the calculated value. Depending on the machine, this cost can be the sum of:
The cost of setting up the working call stack framework.
The cost of comparing n to 0.
The cost of subtracting 1 from n.
The cost of setting up the recursive call stack framework. (As above.)
The cost of multiplying the result of the recursive to factorial call by n.
The cost of storing the returned result so that it can be used by the calling context.
In an unmemorized implementation, each call higher than factorial includes the cumulative cost of steps 2 through 6 proportional to the initial value of n.
A memorized version of the factorial function follows:

In this particular example, if factorial is first invoked with 5, then invoked later with a value less than or equal to five, these return values will also have been remembered, since factorial will have been called recursively with the values 5, 4 , 3, 2, 1 and 0, and the return values for each of these will have been stored. If it is then called with a number greater than 5, such as 7, only 2 recursive calls will be made (7 and 6), and the value for 5! will have been stored from the previous call.
In this way, memoization allows a function to become more time efficient as it is called more often, leading to eventual overall speedup.
Exercise 20
And here's a little exercise combining everything you've seen recursion, crossover and memoization.
There are oranges in the kitchen and you have decided to eat some of these oranges every day as follows:
- Eat an orange.
- If the number of remaining oranges n is divisible by 2 then you can eat n/2 oranges.
- If the number of remaining oranges n is divisible by 3 then you can eat 2*(n/3) oranges.
You can only choose one of the actions per day.
Given the integer n, returns the minimum number of days to eat n oranges.
Input: n = 10
Output: 4
Explanation: You have 10 oranges.
Day 1: Eat 1 orange, 10 – 1 = 9.
Day 2: Eat 6 oranges, 9 – 2*(9/3) = 9 – 6 = 3. (Since 9 is divisible by 3)
Day 3: Eat 2 oranges, 3 – 2*(3/3) = 3 – 2 = 1.
Day 4: Eat the last orange 1 – 1 = 0.
It takes at least 4 days to eat all 10 oranges.


