Contenido
PalancaEjercicios corregidos: algoritmo recursivo
Los siguientes ejercicios corregidos se refieren al principio del algoritmo recursivo, por ejemplo Fibonacci, las Torres de Hanoi y muchos otros casos Matemáticas. Los ejercicios incluyen recursión simple, recursión de cola, recursión cruzada o recursión mutua, y el principio de memorización (para más detalles sobre este último punto, consulte el principio de programación dinámica).

Ejercicio 1
Reescriba los siguientes algoritmos en forma recursiva en forma terminal cuando sea posible.



Una última para el camino. ¡Esta vez tienes que entender lo que hace antes de convertirlo en terminal recursivo!

Consideramos que n es un entero positivo o cero.


algo3 ya es recursivo pero no terminal. Dado que el algoritmo devuelve 2^no, cambiaremos su estructura para convertirlo en terminal.

Por el último algoritmo, primero debemos entender que calcula el mcd entre a y b. Haga una prueba a mano, comprenderá que la primera rama es inútil, por lo que la eliminaremos para la recursividad. La variable r no está presente para reemplazar el valor de a y b, por lo que no encajará en la recursividad.

Ejercicio 2
El problema de Fibonacci (1170 – 1250):
“Teniendo originalmente una pareja de conejos, ¿cuántas parejas obtienes en doce meses si cada pareja genera una nueva pareja cada mes a partir del segundo mes de su existencia? Los conejos nunca mueren.
Entonces, si tomamos un ejemplo de los primeros 7 meses.
Mes | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Pareja | 1 | 1 | 2 | 3 | 5 | 8 | 13 |
a – Expresar la población de parejas del mes n en función de los meses anteriores.
b – Escriba un algoritmo iterativo que calcule el número de parejas después de 12 meses.
c – Modifique el algoritmo iterativo para calcular el número de meses después de los cuales la población de parejas de conejos supera los 300.
d – Escribe el algoritmo recursivo para calcular el número de parejas de conejos después de n meses.
posee -
El número de parejas de conejos en el mes n es la suma de las parejas existentes el mes anterior (en el mes n − 1) y las parejas nuevas en el mes n.
Sin embargo, el texto especifica que todas las parejas existentes dos meses antes (en el mes n − 2) se reproducen.
Por tanto, en el mes n ≥ 2 el número de conejos es igual a la suma del mes n-1 y n-2. En el mes 0 y el mes 1, solo hay un par.
b-

contra -

d-

Es posible hacer Fibonacci en forma terminal:

O usando la memorización:

Ejercicio 3
a – Escribe un algoritmo que calcule el máximo de 2 números reales
b – Escribe un algoritmo recursivo que calcule el máximo de 3 números reales usando el algoritmo de a. Mostrar árbol de llamadas.
c – Escribe un algoritmo recursivo que calcule el máximo de 4 números reales usando el algoritmo de a. Mostrar árbol de llamadas.
d – ¿El algoritmo es recursivo?
posee -

b-

Aquí, Maximum2 actúa como la condición terminal del algoritmo recursivo. La pila de llamadas es la siguiente:

contra -

La pila de llamadas es la siguiente:

d – Aunque parece una recursividad, es más una sobrecarga de función o una llamada de función para reducir el tamaño del problema. No es un algoritmo recursivo per se.
Ejercicio 4
a – ¿Están los algoritmos por debajo de los algoritmos recursivos?
b – ¿Son terminales?
c – ¿Terminan?



posee -
Los algoritmos log y sum son recursivos: cada uno contiene al menos una llamada a sí mismo, por otro lado, power no lo es: llama al algoritmo entonces. Es necesario reemplazar luego por energía.
b-
log es terminal, power y sum no lo son porque requieren cálculo durante la recursividad.
contra -
log termina para cualquier entero x. La iteración de la división de enteros por 2 conduce a 0, y el caso base 0 termina con la ejecución de return.
Para el algoritmo de potencia (corregido), el caso base 0 finaliza con la ejecución de return. Si el algoritmo termina para el valor n−1, también termina para el valor n está ejecutando return. No olvide que un usuario puede ingresar cualquier cosa como potencia (2, – 5), por lo que debe verificar su terminación.
sum no termina cuando n es estrictamente positivo. De hecho, el algoritmo para n termina solo si el algoritmo termina para n+1. Sin embargo, no existe un entero estrictamente positivo para el cual el algoritmo se detenga.
Ejercicio 5
a – Queremos escribir una función recursiva que calcule el cuadrado de un número entero. Para hacer esto, tendremos que usar una relación entre cuadrado(n) y cuadrado(n-1) sabiendo que cuadrado(1)=1. Representa la pila de llamadas para carre(5).
b – Las combinaciones son un concepto matemático que describe las diferentes formas de elegir un número dado de objetos de un conjunto de tamaño dado. Por ejemplo, cuánto es posible sacar 6 bolas de Lotto de 60 en el carrete. O saca 3 cartas de una baraja de tarot. La combinación de elegir p elementos de n elementos se denota C(p,n)=(n/p)*C(p-1, n-1). Obtuvimos C(0,n)=1 y C(n,n)=1.
Escriba la función recursiva no terminal, luego la función recursiva terminal y muestre la pila de llamadas para C(3,7). A través de la función terminal, deducir la función iterativa.
c – Para las combinaciones, generalmente preferimos evitar el método b porque las divisiones pueden crear problemas de redondeo. En su lugar, utilizaremos la siguiente relación: C(p,n)=C(p,n-1)+C(p-1,n-1). Escriba la función recursiva y la pila o árbol pide C(2,4).
a – Para encontrar un vínculo entre cuadrado(n) y cuadrado(n-1), usamos la fórmula: (n+ 1)² = n² + 2n+ 1. Lo escribimos en función de n a n-1: n² = (n−1)²+2(n−1)+1 por lo tanto cuadrado(n)=cuadrado(n-1)+2*n-1. Eso es todo !

La pila de llamadas es:

b – Todo está dicho en el enunciado, sólo resta anotarlo.

Aquí está la lista de llamadas para C(3,7):

Y ahora para la versión de terminal, es un poco más complicado porque tienes que preguntarte qué tienes que guardar en la memoria para la recursividad. En cada iteración hicimos n/p veces la anterior, entonces n/p * (n-1)/(p-1). Podríamos haberlo escrito n(n-1)/p(p-1). Entonces podríamos almacenar la multiplicación de n decreciente en un lado y p decreciente en el otro.

Aquí está la pila de llamadas para C(3,7,1,1):

Deducimos la función iterativa de la función terminal. Simplemente haga un hasta que se alcance la condición de parada.

c – Ya tenemos la relación recursiva en el enunciado.

Aquí está el árbol de llamadas para C(2,4):

Ejercicio 6
Definimos la función de McCarthy de la siguiente manera:

¿Qué hace la función para n>100? para n=98, 99, 100? En general para n<=100?
Vamos a hacer un poco de matemática... Si n > 100 tendremos n-10. El problema surge cuando empezamos con n<=100. Calcula para 98, 99 y 100. Haremos una demostración directa.
Para n entre 90 y 100 inclusive, es decir, 11 valores consecutivos, esto será útil más adelante. Haremos Carthy(Carthy(n+1)) por lo que excederemos el valor de 100. Entonces tendremos Carthy(n+1) al final. Si n+1 aún no es mayor que 100, volvemos a colocar la tapa. Entonces paramos cuando pasamos de 100 a 101, o Carthy(101)=101-10=91.
En resume lo que dejamos al principio del párrafo anterior. Sobre los últimos 11 valores consecutivos, tendremos un resultado de 91. Observamos que cualquier número entre 0 y 89, al que le sumamos 11 siempre que sea menor que 90, tendrá un valor final entre 90 y 100 inclusive.
Deducimos que Carthy en un valor de 100 o menos dará el valor de 91.
Necesitaba un poco de matemática. ¡La informática es solo otra forma sintáctica de hacer matemáticas!
Ejercicio 7
Hablamos de recursión se cruzan cuando dos funciones se llaman recursivamente.
Probaremos en una recursividad cruzada para saber si un número es par (verdadero) o impar (falso). Aquí está la propuesta:

Pruebe par (2), impar (3), par (3) e impar (2). ¿Es correcto el algoritmo? De lo contrario cámbialo para comprobar la corrección ← PD: si el profesor pregunta eso es porque el algo tiene un problema CQFD
Obviamente el algoritmo no es correcto. Tome par (3) → impar (2) → par (1) → impar (0) → par (-1) → impar (-2) → etc. Esto se debe a que las condiciones de parada solo funcionan si el número del método par es par y el método impar es impar. Solo cambiaremos el método impar.

¡Depende de usted volver a probar si es correcto ahora!
Para tener un algoritmo más robusto, sería necesario comprobar que el número entero de entrada sea positivo (o hacer el valor absoluto).
En el caso de una entrada con doble o flotante, es posible completarla redondeándola. Para hacer esto, necesita saber el número después del punto decimal con el siguiente cálculo coma=n*10[10]. Si la coma <5 entonces convertimos (entero) n; de lo contrario, convertimos (entero) n + 1.
Ejercicio 8
Es imposible concluir sobre el recursivo sin mencionar las famosas Torres de Hanoi (¡la obsesión de los estudiantes y, a veces, también de los profesores y profesores!). Así que vamos a tomarlo con calma.

Hay n bandejas de diferentes tamaños y 3 varillas, numeradas del 0 al 2.
Inicialmente, todas las bandejas están ubicadas en el vástago i. El objetivo es transferirlos al varilla j, respetando las siguientes reglas:
– Solo puedes mover un tablero a la vez.
– Las bandejas deben estar siempre dispuestas en tamaño decreciente sobre una varilla (las más grandes en la parte inferior y luego en orden decreciente subiendo sobre la varilla).
1 – Resuelva el problema a mano si n = 2, i = 0 y j = 2 (entonces 2 bandejas, todas están basadas en la barra 0 y queremos ponerlas en la barra 2).
2 – Resuelva el problema a mano si n = 3, i = 0 y j = 2 (entonces 3 bandejas, todas están basadas en la barra 0 y queremos ponerlas en la barra 2).
3 – Supongamos que un amigo tuyo sabe cómo resolver el problema para algún n, y cualquier que i y j. Se le pide que resuelva el problema para n + 1. Tiene derecho para utilizar la ayuda de su amigo. ¿Cómo lo haces?
4 – Escribe la función recursiva que resuelve este problema para todo n, i, j (Si puedes hacerlo sin hacer trampas, ¡enhorabuena! De lo contrario es normal, casi todos pasamos por ese gran momento de incomprensión y cuestionamiento de su carrera…)
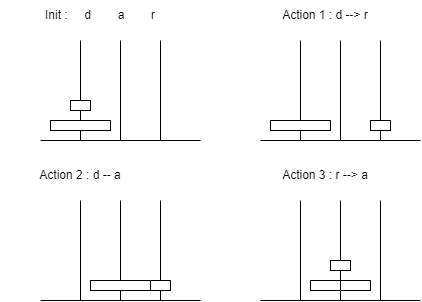
1 –
El tablero pequeño se transfiere de 0 a 1.
El tablero grande se transfiere de 0 a 2.
Pasamos la bandeja chica del 1 al 2.
2 –
El tablero pequeño se transfiere de 0 a 2.
Transferimos la meseta promedio de 0 a 1.
Pasamos el tablero pequeño del 2 al 1. (movimos 2 tableros del 0 al 1).
El tablero grande se transfiere de 0 a 2.
El tablero pequeño se transfiere de 1 a 0.
Pasamos el tablero mediano de 1 a 2.
Pasamos el tablero pequeño del 0 al 2. (movimos 2 tableros del 1 al 2).
3 –
Movemos n bandejas desde i hasta la ubicación que no es ni i ni j (mediante la serie de tres manipulaciones del punto 2). Luego movemos el último tablero (el más grande) de i a j. Le pedimos al amigo que mueva las n bandejas a j.
4 –
Si encuentras eso… ¡champaña! Renombraremos para mayor facilidad los tallos en d para el inicial, a para el de llegada y r para el restante

Veamos cómo funciona, aquí está la estructura general del algoritmo:
Tomemos, por ejemplo, Hanoi(2,d,a,r), que denota el conjunto de recursiones con el orden básico (d,a,r), incluso si esto no tiene sentido para un peso de vista recursivo:
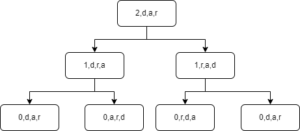
Tenga en cuenta que los nodos con un valor n de 0 no sirven porque la función estará vacía.
Ahora tomemos el árbol con el orden de acciones. Para atravesar el árbol, hagamos un recorrido del árbol.

Un nodo realiza su acción cuando pasamos por debajo de él:
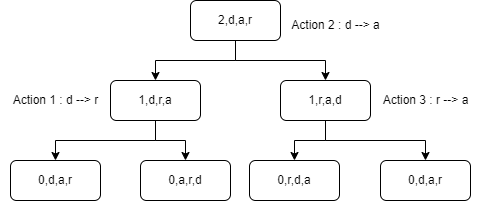
Lo que daría los siguientes movimientos:
Ejercicio 9
Escriba un programa para encontrar el MCD de dos números usando recursividad.
Aquí está la idea detrás del algoritmo:
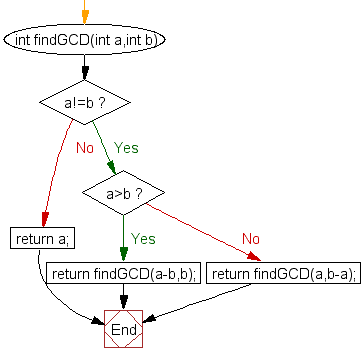
Lo que da el siguiente algoritmo:

También es posible hacer el módulo directamente (en lugar de ab varias veces) para hacer una recursividad con el resto:

Ejercicio 10
Escriba un programa para convertir un número decimal a binario usando recursividad.
Aquí está la idea detrás del algoritmo:
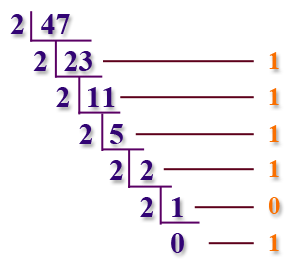

Ejercicio 11
Escriba un programa para encontrar el MCM de dos números usando recursividad.

Aquí está el algoritmo:
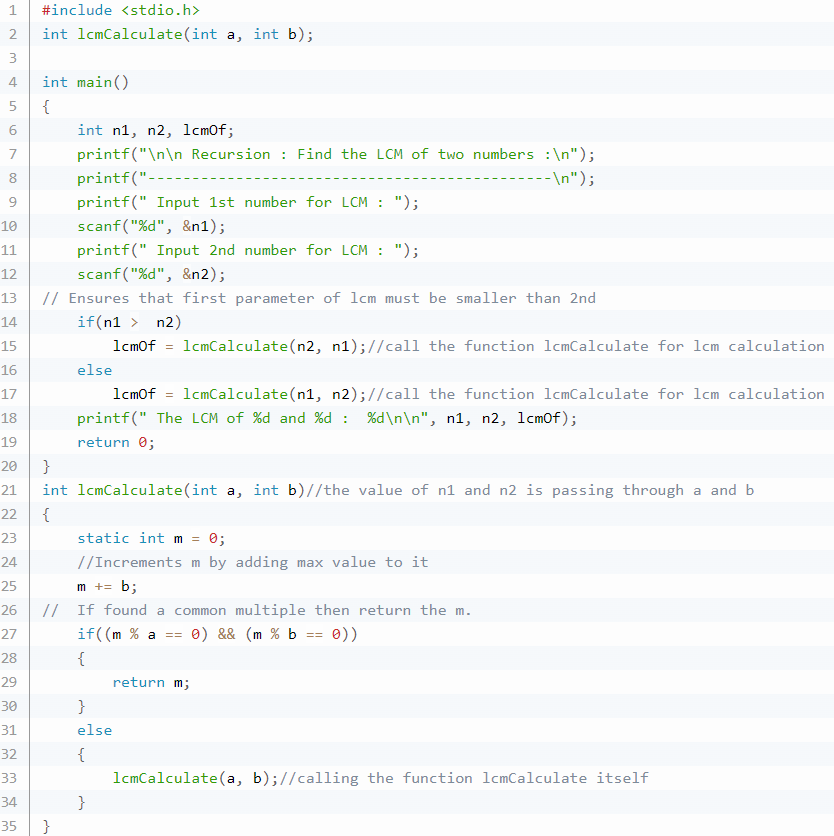
La función recursiva lcm() toma dos números enteros como argumentos. Tome una variable estática m e inicialícela con cero, luego actualícela con uno de los números. Aquí actualizamos la variable m con b, por lo que la variable m siempre será divisible por la variable b. Por lo tanto, necesitamos verificar solo con la variable a, es decir (m%a == 0).
Como estamos sumando el número más grande a la variable m, entonces la variable b debe contener el número más grande. Al llamar a lcm(), debemos pasar el número menor como a y el número mayor como b.
Si sumamos el número mayor, el número de llamadas recursivas será el mínimo, pero si sumamos el número menor, el número de llamadas recursivas será mayor que en el caso anterior. Sabemos que menos llamadas recursivas dan un alto rendimiento.
Tomemos el ejemplo de los números 3 y 7. Si sumamos el número mayor 7 a la variable de suma, entonces,
0+7 = 7 (llamada desde la función principal), 7%3 != 0
7+7 = 14 (primera llamada recursiva), 14%3 != 0
14+7 = 21 (segunda llamada recursiva)
21 es divisible por 3 y 7
Entonces solo habrá 2 llamadas recursivas.
De manera similar, si tomamos el número más pequeño (3), entonces,
0+3 = 3 , 3%7 != 0
3+3 = 6 , 6%7 != 0
6+3 = 9 , 9%7 != 0
9+3 = 12 , 12%7 != 0
12+3 = 15 , 15%7 != 0
15+3 = 18 , 18%7 != 0
18+3 = 21
21 es divisible por 3 y 7
Por tanto, habrá 6 llamadas recursivas.
Ejercicio 12
Escriba un programa para verificar si una cadena dada es Palindrome o no.
Ejercicio 13
El número Pi se puede calcular mediante la siguiente fórmula:
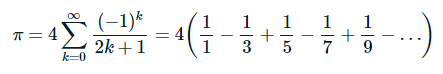
Escriba un algoritmo recursivo para calcular el valor de Pi considerando la secuencia hasta el rango n.
Haz lo mismo con las siguientes aproximaciones de Pi.
Serie de Gregory-Leibniz:

Y la serie anterior de Madhava, Ramanujan, David y Chudnovsky (el factorial será una llamada recursiva por derecho propio):

Aquí está el algoritmo recursivo:
gregorio(n)
{
si (n==0) devuelve 4
devolver 4*pow(-1,n)/(2*n+1)+gregorio(n-1)
}
Las otras fórmulas siguen el mismo principio, no es necesario detallarlo todo. ¡Tenga cuidado de todos modos de usar el cálculo correcto en la recursividad! (los algoritmos serán más fáciles de escribir en recursivo no terminal.
Ejercicio 14
En la década de 1920, Wilhelm Ackermann y Gabriel Sudan, entonces estudiantes de David Hilbert, estudiaron los fundamentos de la computabilidad. Sudán es el primero en dar un ejemplo de una función primitiva recursiva pero no recursiva, luego llamada función de Sudán. Poco después y de forma independiente, en 1928, Ackermann publicó su propio ejemplo de una función primitiva recursiva pero no recursiva. Originalmente, Ackermann considera una función ϕ(m, n, p) dependiente de tres variables.
Más tarde, Rózsa Péter y Raphael Robinson dan una función de solo dos variables; es esta última la que se conoce hoy como la función de Ackermann.
La función de Ackermann-Péter se define recursivamente de la siguiente manera:

¡La función crece tan rápido que es rápidamente imposible escribirla con un número clásico y es necesario usar la notación de Knuth!

La solución es muy simple, pero no recomiendo ejecutar el algoritmo en una PC.
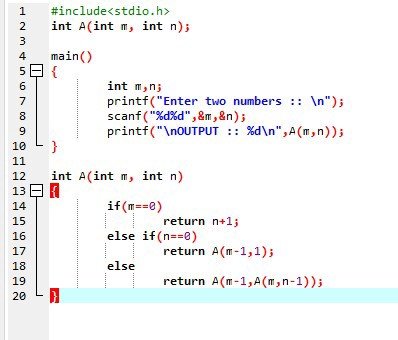
Ejercicio 15
Aquí está la función de Sudán, otro alumno de David Hilbert. Esta función fue diseñada en 1927, un año antes que la función de Ackermann.
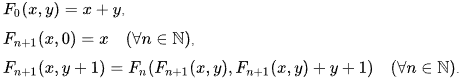
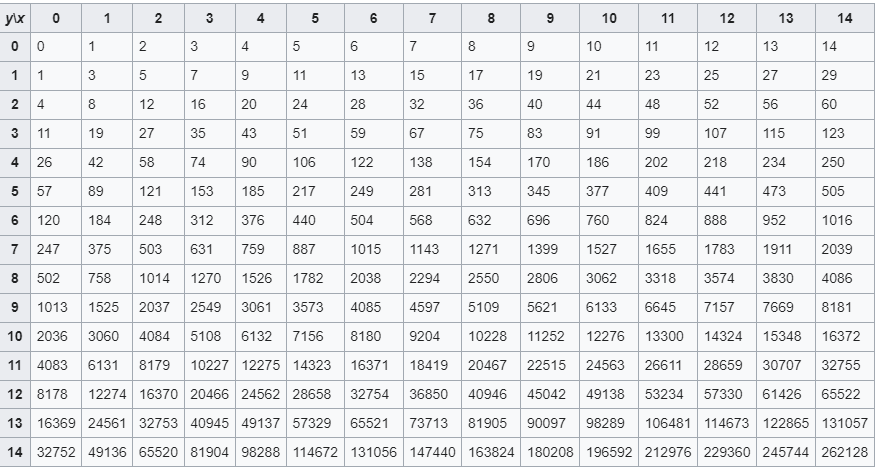
Aquí, cuanto más crece el valor de n, más explota el resultado de la función de la función. Aquí está el ejemplo para F_1(14,14).
Nada muy complicado, solo copia la fórmula matemática en forma de recursividad.

Ejercicio 16
La función de Takeuchi, abreviada tak o, a veces, tarai, es la presentación recursiva de una función que lleva el nombre de Ikuo Takeuchi (竹内郁雄). La presentación de la función, que además admite una definición no recursiva bastante simple, puede requerir cálculos muy largos si el compilador que la implementa no es eficiente. Por esta razón, a menudo se usa para probar el rendimiento de la implementación de funciones recursivas por parte del compilador de un lenguaje de programación.
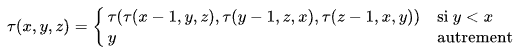
La definición original de Takeuchi era:

tarai es la abreviatura de "pasar por ahí" en japonés. John McCarthy llamó a esta función tak() en honor a Takeuchi.
La recursividad se ha mejorado gracias a la recursividad cruzada:

Ejercicio 17
La secuencia de Hofstadter macho-hembra está definida por:
F(0)=1, M(0)=0 y
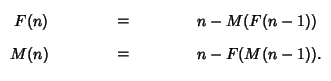
Escribe un algoritmo recursivo para calcular la sucesión de Hofstadter.
Lo mismo para la secuencia G:

Este es un algoritmo recursivo cruzado (también llamado perfecto).

Para la secuencia G, el principio es el mismo:

A continuación se muestra un ejemplo de un árbol de nodos formado cuando el programa se ejecuta con valores de n entre 1 y 21. Por ejemplo, G(15) producirá el valor 9 y G(9) producirá el valor 6, etc. . Curiosamente, la secuencia de Fibonacci es visible en el lado derecho del árbol.
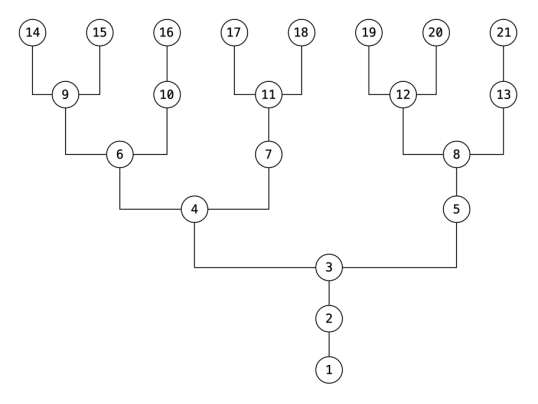
Ejercicio 18
Algunos lenguajes de programación permiten la memorización. Es un almacenamiento en caché de los valores de retorno de una función según sus valores de entrada. El objetivo de esta técnica de optimización de código es reducir el tiempo de ejecución de un programa informático mediante la memorización de los valores devueltos por una función.
Así, realizando la secuencia de Fibonacci, es posible memorizar los valores ya calculados para evitar saturar la memoria con valores ya obtenidos en otra rama del árbol de llamadas.
De hecho, cada vez que calculamos fib(i), podemos almacenar en caché ese resultado y usarlo más tarde. Entonces, cuando llamamos a fib(n), no deberíamos tener que hacer mucho más que llamadas 0(n), porque solo hay O(n) valores posibles que podemos enviar a fib(n).

Aquí el árbol de recursividad será muy diferente al de la variante no terminal:
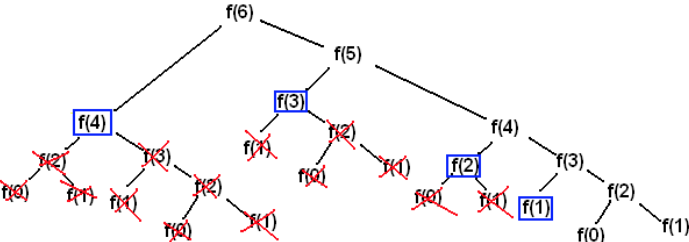
Tenga en cuenta que el árbol de arriba no tiene en cuenta la dirección de la llamada izquierda y luego la llamada derecha. Para mayor comodidad, se acostumbra poner la primera llamada como hijo izquierdo y la segunda como hijo derecho, por lo tanto ¡lo opuesto al árbol presentado!
Los tiempos de cálculo se reducen considerablemente como se muestra en el siguiente diagrama sobre Fibo(100) en sus variantes:
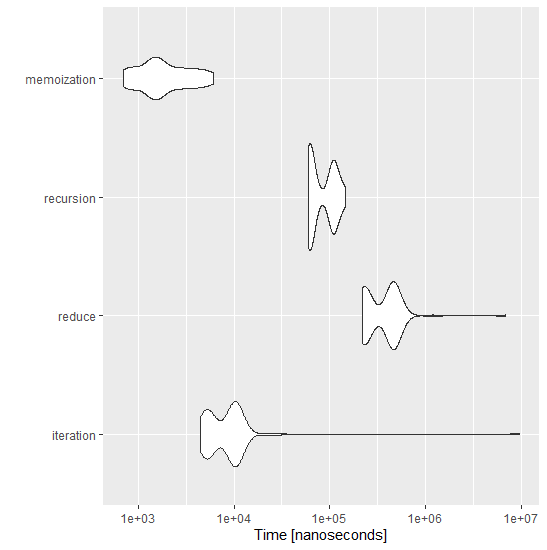
Ejercicio 19
Algunos lenguajes de programación permiten la memorización. Es un almacenamiento en caché de los valores de retorno de una función según sus valores de entrada. El objetivo de esta técnica de optimización de código es reducir el tiempo de ejecución de un programa informático mediante la memorización de los valores devueltos por una función.
Escriba un algoritmo que calcule el factorial n (n!) utilizando el principio de memorización.
Aquí está la solución clásica para realizar cálculos factoriales recursivos:

La implementación no memorizada anterior, dada la naturaleza del algoritmo recursivo involucrado, requeriría n + 1 invocaciones de factoriales para llegar a un resultado, y cada una de estas invocaciones, a su vez, tiene un costo asociado en términos de tiempo requerido para la ejecución. función. para devolver el valor calculado. Dependiendo de la máquina, este costo puede ser la suma de:
El costo de configurar el marco de la pila de llamadas funcional.
El costo de comparar n con 0.
El costo de restar 1 de n.
El costo de configurar el marco de pila de llamadas recursiva. (Como anteriormente.)
El costo de multiplicar el resultado de la llamada recursiva a factorial por n.
El costo de almacenar el resultado devuelto para que pueda ser utilizado por el contexto de llamada.
En una implementación no memorizada, cada llamada mayor que factorial incluye el costo acumulativo de los pasos 2 al 6 proporcional al valor inicial de n.
A continuación se muestra una versión memorizada de la función factorial:

En este ejemplo en particular, si primero se invoca factorial con 5, luego se invoca después con un valor menor o igual a cinco, estos valores de retorno también se habrán recordado, ya que factorial se habrá llamado recursivamente con los valores 5. , 4 , 3, 2, 1 y 0, y se habrán almacenado los valores de retorno para cada uno de estos. Si luego se llama con un número mayor que 5, como por ejemplo 7, solo se realizarán 2 llamadas recursivas (7 y 6), ¡y el valor de 5! habrán sido almacenados de la llamada anterior.
De esta manera, la memorización permite que una función sea más eficiente en el tiempo a medida que se llama con más frecuencia, lo que eventualmente conduce a una aceleración general.
Ejercicio 20
Y aquí hay un pequeño ejercicio que combina todo lo que has visto recursividad, cruce y memorización.
Hay naranjas en la cocina y has decidido comer algunas de estas naranjas todos los días de la siguiente manera:
- Come una naranja.
- Si el número de naranjas restantes n es divisible por 2, entonces puedes comer n/2 naranjas.
- Si el número de naranjas restantes n es divisible por 3, entonces puedes comer 2*(n/3) naranjas.
Solo puedes elegir una de las acciones por día.
Dado el entero n, devuelve el número mínimo de días para comer n naranjas.
Entrada: n = 10
Salida: 4
Explicación: Tienes 10 naranjas.
Día 1: Come 1 naranja, 10 – 1 = 9.
Día 2: Come 6 naranjas, 9 – 2*(9/3) = 9 – 6 = 3. (Ya que 9 es divisible por 3)
Día 3: Come 2 naranjas, 3 – 2*(3/3) = 3 – 2 = 1.
Día 4: Come la última naranja 1 – 1 = 0.
Se necesitan al menos 4 días para comer las 10 naranjas.


