Proceso de Markov 101

Proceso de Markov

Un proceso de Markov representa todos los procesos que tienen argumentos de experiencia aleatorios.

Un experimento aleatorio, indicado con E, es un experimento cuyo resultado está sujeto al azar. Denotamos por Ω el conjunto de todos los posibles resultados de este experimento, y se denomina universo, espacio de posibilidades o incluso espacio de estados. Un resultado de E es un elemento de Ω anotado ω.

Por ejemplo, en el juego de lanzamiento de moneda, el universo de la experiencia de "lanzar una moneda" es Ω = {P, F}. Para el experimento "lanza dos monedas una tras otra", el universo es Ω = {PP, PF, FP, FF}.

Un evento aleatorio A vinculado al experimento E es un subconjunto de Ω que se puede decir a la luz del experimento si se realizó o no. En el ejemplo anterior, el evento aleatorio de “sacar cara” en el lanzamiento de una moneda se puede observar fácilmente lanzando una moneda. Un evento aleatorio es un conjunto y, por tanto, tiene las principales propiedades de la teoría de conjuntos.

Operaciones elementales sobre las partes de un conjunto:

• Intersección: la intersección de los conjuntos A y B señalados A ∩B es el conjunto
  puntos pertenecientes tanto a A como a B.
• Reunión: la reunión de dos conjuntos A y B denotados A∪B es el conjunto de
  puntos pertenecientes a al menos uno de los dos conjuntos.
• Conjunto vacío: el conjunto vacío, anotado Ø, es el conjunto que no contiene
  elemento.
• Conjuntos disjuntos: se dice que los conjuntos A y B son disjuntos si A ∩B = Ø.
• Complementario: el complementario del conjunto A ⊂ Ω en Ω, denotado por A^vs donde Ω \ A, es el conjunto de elementos que no pertenecen a A. Los conjuntos A
  y A^vs son disjuntos.

Establecer operaciones:

• No: la ocurrencia del evento contrario a A está representada por A^vs: los
  El resultado del experimento no pertenece a A.
• Y: el evento “A y B se logran” está representado por A∩B; el resultado de
  la experiencia se encuentra tanto en A como en B.
• O: el evento "A o B se logra" está representado por A∪B; el resultado
  hay experiencia en A o B o en ambos.
• Implicación: el hecho de que la realización del evento A conduce a la realización
  de B se traduce en A ⊂ B.
• Incompatibilidad: si A∩B = Ø, se dice que A y B son incompatibles. Un resultado de
  la experiencia no puede ser tanto en A como en B.

Con cada evento buscamos asociar una medida (que no definiremos en este curso) entre 0 y 1 y que represente la probabilidad de que ocurra el evento. Para un experimento A, esta medida se denota P (A).

Formalmente, sea E un experimento aleatorio del universo Ω. Llamamos a una medida de probabilidad en Ω (o más simplemente probabilidad) una aplicación P que asocia con cualquier evento aleatorio A un número real P (A) tal que
(i) Para cualquier A tal que P (A) existe, tenemos 0 ≤ P (A) ≤ 1.
(ii) P (Ø) = 0 y P (Ω) = 1.
(iii) A∩B =; implica que P (A ∪B) = P (A) + P (B).

La probabilidad de un evento puede entenderse como P (A) = número de casos factibles / número de casos posibles. El "número de casos" es el cardinal de un evento / universo.

Variables aleatorias y probabilidad

Una variable aleatoria es una función cuyo valor depende del resultado de una
experimento aleatorio E del universo Ω. Decimos que una variable aleatoria X es discreta si toma un número finito o contable de valores. El conjunto de cuestiones ω en las que X toma un valor fijo x forma el evento {ω: X (ω) = x} que denotamos por [X = x]. La probabilidad de este evento se anota P (X = x).

La función p_X : x → P (X = x) se llama ley de la variable aleatoria X. Si {x₁, X₂,…} Es el conjunto de valores posibles para X, tenemos:

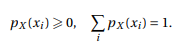
Deje S₂ el número de pilas obtenidas al lanzar dos monedas. El conjunto de valores posibles para S₂ es {0,1,2}. Si proporcionamos el universo Ω asociado con este experimento aleatorio con la probabilidad uniforme P, surgen las siguientes soluciones:

Cuando existe (la expectativa siempre se define si X toma un número finito de valores, o si X tiene valores positivos), llamamos a la expectativa o promedio de una variable aleatoria discreta X la cantidad indicada E (X) definida por:

Cuando existe, llamamos a la varianza de una variable aleatoria discreta X la
cantidad indicada Var (X) definida por:

La idea básica del condicionamiento es la siguiente: la información adicional sobre la experiencia cambia la probabilidad que se le da al evento estudiado.

Por ejemplo, para una tirada de dos dados (uno rojo y otro azul), la probabilidad de
el evento "la suma es mayor o igual a 10" es igual a 1/6 sin información
adicional. Por otro lado, si sabemos que el resultado del dado rojo es 6, es
igual a 1/2 mientras que es igual a 0 si el resultado del dado rojo es 2.

Sea P una medida de probabilidad en Ω y B un evento tal que P (B)> 0. El
probabilidad condicional de que A conozca a B es el P (A | B) real definido por:

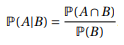
Se dice que los eventos A y B son independientes si:

Podemos extender el independiente an eventos. Deja A₁, PARA₂,…, PARA_no eventos. Se dice que son independientes (como un todo) si para cualquier k ∈ {1,…, n} y para cualquier conjunto de enteros distintos {i₁,…, I_k } ⊂ {1,… n}, tenemos:

Las variables aleatorias pueden ser independientes de dos en dos, sin ser independientes en su conjunto: