Apoyo a la toma de decisiones 101

Ayuda con la decisión

Cualquier problema industrial consiste, bajo determinadas condiciones, en maximizar el beneficio o minimizar el gasto. En este contexto, la ganancia y el gasto no siempre se refieren a una variable monetaria, también se puede expresar por tiempo, distancia u otras.

Muy a menudo, el problema se plantea de manera burda, es decir, mediante un texto o una especificación. El fabricante no era un experto en el campo de la redacción de un problema matemático, las especificaciones incluyen todo tipo de datos, útiles o no para su modelado.

Incluso en el contexto en el que usted mismo es el patrocinador, es posible que no conozca el alcance de su problema y, a lo largo del curso del agua, descubra las diversas limitaciones y variables que debe enfrentar.

Otro problema surge una vez que el modelo matematico llevado a cabo: ¿qué herramienta informática se utilizó para resolver este problema? qué algoritmo Elegir ? su simulación? su complejidad ? su optimidad?

Por lo tanto, construir y resolver un problema industrial requiere rigor, flexibilidad mental y seguir un proceso de modelado preciso.

Optimización y apoyo a la toma de decisiones

Un problema D es decidir si la respuesta es binaria: Sí o No. Denotamos Sí (D) todas las instancias a las que respondemos Sí.

Considere el siguiente problema de decisión: sea un grafico G ponderado, ¿hay un árbol ¿cubierta? Sí (D) = {subgrafo conectado no cíclico de G}. El problema: la existencia de un cubierta de árboles de peso ≤ k es también un problema de decisión. El problema de optimización es encontrar el valor k tal que sea mínimo.

Para comprender mejor los dos conceptos, tomaremos un ejemplo: desea realizar una gira por Europa, visitando un cierto número de ciudades en un período de 6 meses. Además, desea permanecer un tiempo determinado en cada lugar para poder visitar las zonas turísticas y admirar el paisaje.

Este tipo de problemas tiene diferentes formas de modelarse en función de lo que se quiera hacer: ser el más rápido, favorecer zonas densamente turísticas, etc. Una decisión debe seleccionarse entre un conjunto de posibles decisiones para optimizar el criterio elegido.

El modelado incluye una búsqueda de mínimo o máximo, por lo que es una mejoramiento. Todos los problemas de apoyo a la decisión contienen los siguientes tres puntos:

• El tipo de decisión: qué queremos hacer (aquí buscamos una optimización)
• Posibles decisiones: qué se puede hacer (la campo de definición)
• El criterio de selección: cómo se elige (el modelado del problema).

El problema estudiado se ubica en un contexto determinado que se traducirá en parámetros. Todas las relaciones entre estos se muestran en el modelo. Este último puede tomar la forma de un modelo matemático o un gráfico.

El modelado es solo una representación esquemática del problema, solo los elementos considerados relevantes se retienen en la construcción de la decisión. Procede mediante simplificaciones y omisiones.

El entorno del modelo también puede influir. Ya sea determinista o con incertidumbre, está presente a través de leyes de probabilidad, estocásticas, etc. dentro de las limitaciones.

El criterio de selección puede dar lugar a diferentes soluciones en función del parámetro propuesto. En algunos casos, el modelo presenta solo un criterio de selección, esto se denomina investigación operativa.

Todos los modelos constan de tres componentes básicos:

• Las variables de resultado son salidas. Reflejan el nivel de eficiencia del sistema. Son variables dependientes.
• Las variables de decisión describen acciones alternativas.
• Las variables incontrolables son factores que afectan el resultado pero que no están bajo el control de quien toma las decisiones. O estos factores son fijos o pueden variar.

Los componentes están vinculados entre sí por expresiones. Matemáticas en un marco de modelos cuantitativos. Un principio de elección es un criterio que describe la aceptabilidad de una solución de enfoque.

Un modelo puede ser un modelo normativo o un modelo descriptivo. En el primero, la solución elegida es claramente la mejor de todas las alternativas posibles. Para encontrarlo, debemos examinar todas las alternativas y demostrar que la seleccionada es efectivamente la mejor (hablamos de optimización). Los modelos descriptivos estudian acciones alternativas bajo diferentes configuraciones de entrada y proceso. No se verifican todas las alternativas, solo un conjunto dado.

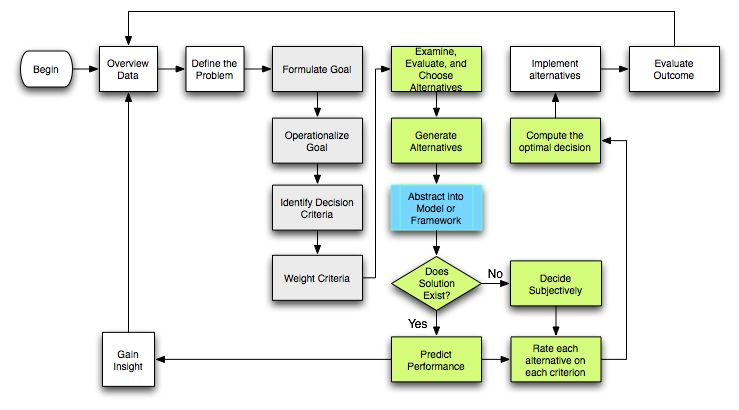
Soporte de soluciones y decisiones

Una vez que se ha creado el modelo y se ha encontrado una solución, es importante analizarlo para validar el modelo. Este último fue solo una representación esquemática del problema, puede no ser adecuado para el propósito previsto. Una solución destaca la validez de las opciones de decisión y las opciones del modelo. Solo el responsable de la toma de decisiones / patrocinador puede validar el enfoque adoptado.

El diagrama del proceso de apoyo a la decisión es el siguiente: