Complejidad del tiempo: sistemas complejos e inteligencia artificial

Contenido

Complejidad del tiempo

La complejidad temporal representa de forma asintótica el tiempo que algoritmo para encontrar una solución.

Sea un problema P y M un método para resolver este problema. El algoritmo es una descripción con estructuras de control y datos que permiten escribir el método M en un lenguaje reconocible por cualquier individuo o máquina.

Como recordatorio, las estructuras de control son: una secuencia, una rama (o selección), un bucle (o iteración). Las estructuras de datos son: constantes, variables, matrices (o espacio de almacenamiento ordenado), estructuras recursivas (listas, gráficos, etc.).

Operación elemental

La complejidad consiste en evaluar la efectividad del método M y comparar este último con otro método M '. Esta comparación es independiente del entorno (máquina, sistema, compilador, lenguaje, etc.). La eficiencia depende del número de operaciones elementales. Éstos dependen del tamaño de los datos y la naturaleza de los datos.

Sea n el tamaño de los datos y T (n) el número de operaciones elementales. La evaluación de la eficacia se realizará en el mejor de los casos, en el peor de los casos y en el caso medio.

En el caso de una estructura de tipo secuencial, la evaluación es igual a la suma de los costos. Por ejemplo, si el algoritmo tiene procesamiento T1 (n) seguido de T2 (n), entonces T (n) = T1 (n) + T2 (n).

En el caso de una sucursal, la evaluación es igual al máximo de sucursales. Por ejemplo, el algoritmo ejecuta T1 (n) de lo contrario T2 (n), luego T (n) = max (T1 (n), T2 (n)).

En el caso de un bucle, la evaluación es igual a la suma de los costos de los pasajes sucesivos. Por ejemplo, si el algoritmo es a "mientras se hace Ti (n) con la complejidad de Ti (n) dependiendo del número i de la iteración. Entonces la complejidad es T (n) = suma (i = 1 an) Ti (n).

Para una versión recursiva, los invito a ir a la página correspondiente. Sea C (n) el procesamiento realizado en una función de divide y vencerás. Entonces la complejidad es T (n) = 2 * T (n / 2) + C (n) = n log (n) si C (n) = n.

Notación Landau

La notación de Landau caracteriza el comportamiento asintótico de una función, es decir, el comportamiento de f (n) cuando n tiende a infinito.

Decimos que f (n) es una gran O de g (n) si

\ existe k> 0, \ existe n_0 \; \ forall n> n_0 \; | f (n) | \ leq | g (n) | \ cdot k

complejidad del tiempo algoritmo de notación big o landau

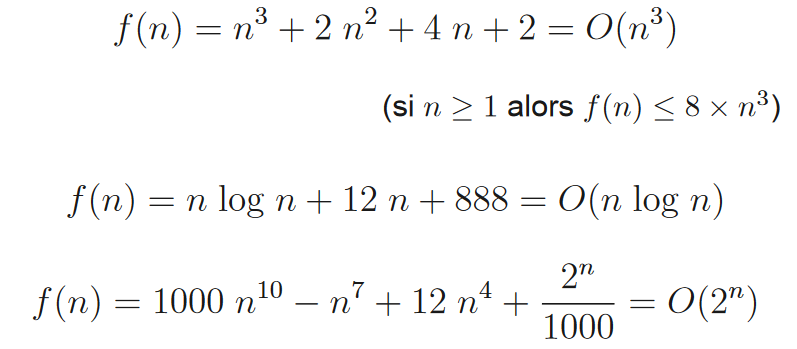
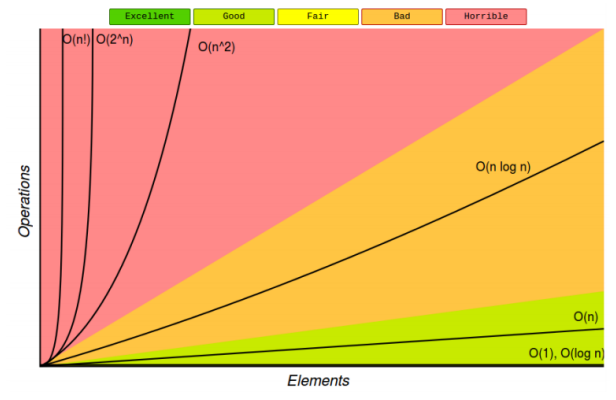
Ejemplos de

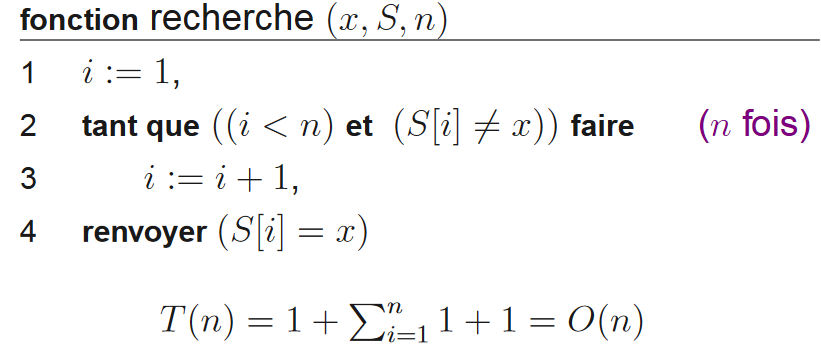
Peor, mejor y promedio

Podemos calcular para la mayoría de los algoritmos una complejidad en el peor de los casos (el mayor número de operaciones elementales), el mejor y en promedio. La media es una suma ponderada por la probabilidad de presencia de posibles complejidades. La mayoría de las veces, usamos la complejidad del peor de los casos porque queremos conocer un límite superior de tiempo de ejecución.

Considere un algoritmo para encontrar un elemento en una matriz en forma iterativa. El algoritmo se detiene cuando se encuentra el valor. El algoritmo se descompone de la siguiente manera: asignación de 0 a i, siempre que i no haya atravesado la matriz, incrementamos i, si tab [i] = valor, devolvemos verdadero, de lo contrario, al final de la matriz devolvemos falso. Sea C la complejidad del cuerpo del bucle.

En el peor de los casos, el algoritmo recorre toda la tabla, es decir, T (n) = 1 + n * C = O (n). En el mejor de los casos, el elemento está al comienzo de la matriz, por lo que T (n) = 1 + C = O (1). Consideramos que, en promedio, hay una probabilidad de 50% de que el elemento no esté en la matriz y 50% de que esté en el medio de la matriz (esto, por supuesto, es absurdo, pero no haremos todas las posibilidades). En este caso, la complejidad en promedio es T (n) = 0.5 * (1 + n * C) + 0.5 * (1 + n * C / 2) = a * n + b con a y b constantes = O (no ). Observamos que el comportamiento asintótico en promedio es el mismo que en el peor de los casos.

Ejemplos de

Suponga que cada una de las siguientes expresiones da el tiempo de procesamiento T (n) empleado por un algoritmo para resolver un problema de tamaño n. Seleccione los términos dominantes con el mayor aumento en n y especifique la complejidad de Big-Oh más baja de cada algoritmo.

Expresión	Dominante	O (.)
5 + 0,001n³+ 0.025n	0.001n³	Nosotros³)
500n + 100n^1.5 + 50n registro₁₀ no	100n^1.5	Nosotros^1.5)
0.3n + 5n^1.5 + 2,5 n^1.75	2,5 n^1.75	Nosotros^1.75)
no² Iniciar sesión₂ n + n (registro₂ no)²	no² Iniciar sesión₂ no	Nosotros² log n)
n registro₃ n + n log₂ no	n registro₃ n, n log₂ no	O (n log n)
3 registro₈ n + log₂ Iniciar sesión₂ Iniciar sesión₂ no	3 registro₈ no	O (log n)
0. 100n + 0.01n²	0.01n²	Nosotros²)
0.01n + 100n²	100n²	Nosotros²)
2n + n^0.5 + 0.5n^1.25	0.5n^1.25	Nosotros^1.25)
0.01n log₂ n + n (registro₂ no)²	n (registro₂ no)²	O (n (log n)²)
Registro de 100n₃ n + n³ + 100n	no³	Nosotros³)

Las instrucciones siguientes muestran algunas características de la notación “Big-Oh” para las funciones f ≡ f (n) y g ≡ g (n). Determine si cada afirmación es VERDADERA o FALSA y corrija la fórmula en el último caso.

Función	¿Verdadero o falso?	Después de corregir
O (f + g) = O (f) + O (g)	FALSO	O (f + g) = max {O (f), O (g)}
O (f g) = O (f) O (g)	CIERTO
si g = O (f) y h = O (f) entonces g = O (h)	FALSO	si g = O (f) yf = O (h) entonces g = O (h)
5n + 8n 2 + 100n 3 = O (n 4)	CIERTO
5n + 8n 2 + 100n 3 = O (n 2 log n)	FALSO	Nosotros³ )