Contenido
PalancaEjercicios corregidos mediante software LARP.
Los siguientes ejercicios corregidos se refieren a la creación de algoritmos según la estructura del diagrama de flujo del software LARP.

Para empezar
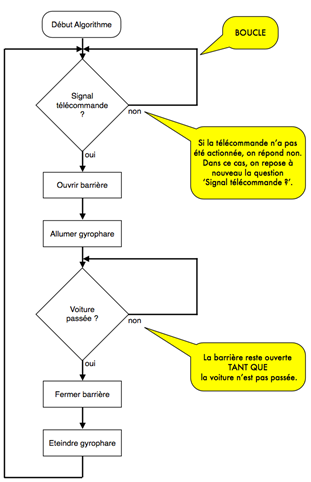
Escriba el diagrama de flujo que permita la siguiente operación:
- Una puerta se abre mediante un mando a distancia.
- El sistema utiliza un sensor de infrarrojos para saber si el coche ha pasado.
- La barrera se cierra cuando el coche ha pasado.
- Una baliza giratoria se enciende cuando la barrera está abierta y se apaga cuando la barrera está cerrada.
Utiliza sólo las acciones y eventos que se enumeran a continuación:
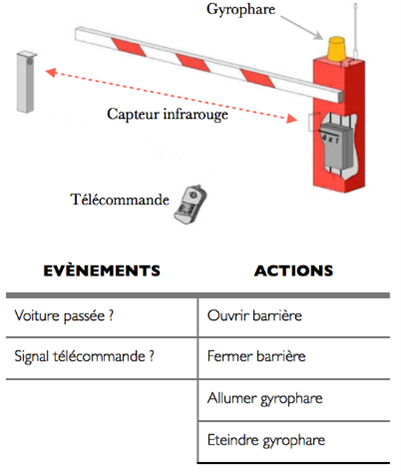
Ejercicio 1
Desafío 1: encontrar el centro de un círculo. Escribe el diagrama de flujo de operaciones para encontrar el centro de un círculo. No está prohibido darle un nombre a tu algoritmo.
Desafío 2: Divide un círculo en 6 partes iguales. Escribe el diagrama de flujo de operaciones que te permita dividir un círculo en 6 partes iguales. No está prohibido utilizar un algoritmo existente si tiene un nombre; Luego podemos llamarlo por su nombre: Ejecutar “myAlgo”.
Desafío 1:
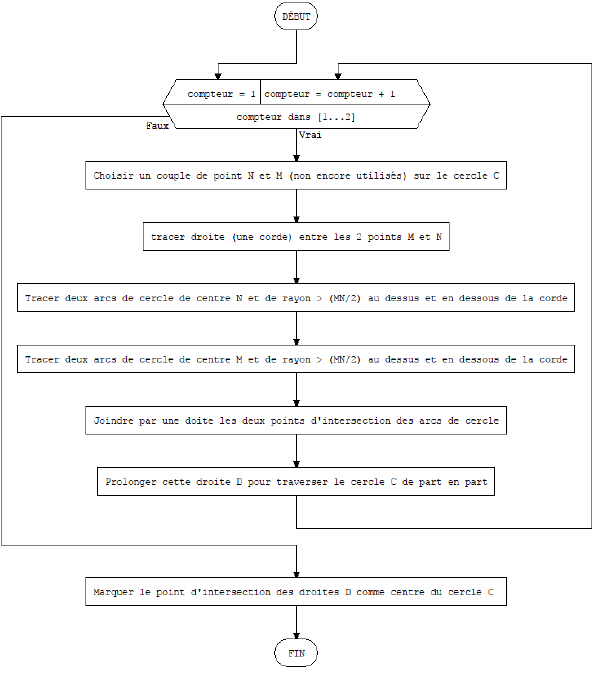
Desafío 2:

Ejercicio 2
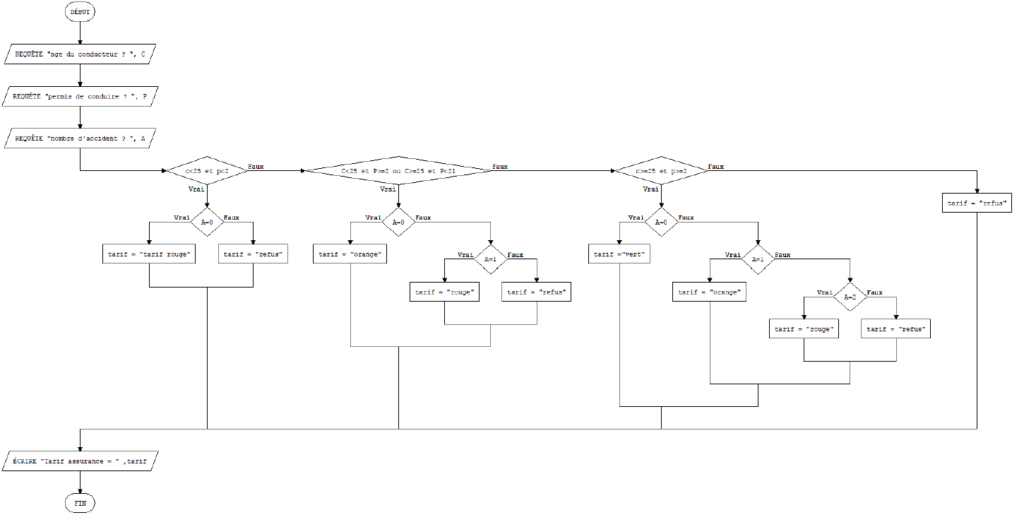
Una compañía de seguros ofrece a sus clientes cuatro tarifas identificables por colores, de menor a mayor: blanco, verde, naranja, rojo.
El precio depende de la situación del conductor:
- Se asigna la tarifa roja al conductor menor de 25 años y con una antigüedad inferior a dos años del permiso, siempre que nunca haya sido responsable de un accidente. En caso contrario, la empresa se niega a asegurarlo.
- Un conductor menor de 25 años y con un permiso de más de dos años, o mayor de 25 años pero con un permiso de menos de dos años, tiene derecho a la tarifa naranja si nunca ha provocado un accidente, a la tarifa roja si accidente, de lo contrario se rechaza.
- Un conductor mayor de 25 años que tenga permiso durante más de dos años se beneficia de la tarifa verde si no es causante de ningún accidente y de la tarifa naranja por un accidente, de la tarifa roja por dos accidentes y de la tarifa rechazada más allá.
Ejercicio 3
Establecer el pseudocódigo del algoritmo que satisface la siguiente necesidad:
El algoritmo comienza preguntándote el importe del préstamo inicial (a interés cero).
Luego registra el importe de sus sucesivos reembolsos.
Con cada reembolso, el algoritmo le envía información: la cantidad de capital que queda por reembolsar.
INICIO
CONSULTA “¿monto del préstamo?” " , mi
MIENTRAS E>0 HACER
SOLICITAR “¿monto de reembolso?” » ,R
SI (ER >=0) ENTONCES
E = RE
ESCRIBA “cantidad restante por reembolsar => “, E
DE LO CONTRARIO
ESCRIBA “su reembolso es demasiado alto”
ESCRIBA “valor máximo => “, E
TERMINARA SI
FINTANTQUE
ESCRIBA “fin del reembolso”
FIN
Ejercicio 4
Desafío 1: Escriba el diagrama de flujo de un algoritmo que solicite al usuario un número y luego muestre su valor absoluto. Pruébelo con números positivos y negativos (maneje el caso del valor 0)
Desafío 2: Escriba un pseudocódigo para un algoritmo que solicite al usuario dos números diferentes y luego muestre el mayor. Pruébelo con pares de números que cubran todos los casos posibles.
Desafío 3: Escriba el diagrama de flujo de un algoritmo que pide al usuario 4 números enteros a, b, c, d. El algoritmo debe dar la solución a la ecuación ax + b = cx + d. O informar al usuario de situaciones especiales para resolver la ecuación. Pruebe el algoritmo en los distintos casos posibles.
Desafío 4: Escribe el pseudocódigo de un algoritmo que pide al usuario 3 números enteros a, b, c. El algoritmo debe dar la(s) solución(es) real(es) de la ecuación ax2 + bx + c = 0. Prueba en varias situaciones posibles.
Desafío 5: Escriba un pseudocódigo para un algoritmo que muestre la lista de cuadrados de números siempre que el cuadrado sea menor que 100
Desafío 6: Escribe el pseudocódigo de un algoritmo que tengamuestra la lista de números enteros múltiplos de 3
Desafío 7: Escribe el pseudocódigo de un algoritmo que tengamuestra la lista de números enteros múltiplos de 3 y 5
Desafío 1:
INICIO
CONSULTA “¿ingresa un número?” " , NO
SI N>0 ENTONCES
val_abs=N
DE LO CONTRARIO
val_abs = -N
TERMINARA SI
ESCRIBA “el valor absoluto de “,N” es “,val_abs
FIN
Desafío 2:
INICIO
CONSULTA "¿un primer número?" » , N1
CONSULTA "¿un segundo número?" » , N2
SI N1>N2 ENTONCES
ESCRIBA N1”, es mayor que “,N2
DE LO CONTRARIO
ESCRIBA N2”, es mayor que “,N1
TERMINARA SI
FIN
Desafío 4:
INICIO
CONSULTA “ingrese el coeficiente a > “, a
CONSULTA “ingrese el coeficiente b > “, b
CONSULTA “ingrese el coeficiente c > “, c
d = b*b – 4*a*c
SI d > 0 ENTONCES
R1 = (-b + RAÍZ(d)) / (2*a)
R2 = (-b + RAÍZ(d)) / (2*a)
ESCRIBIR” hay dos raíces: “,R1” y “,R2
DE LO CONTRARIO SI d=0 ENTONCES
R = (-b) / (2*a)
ESCRIBE “sólo hay una raíz:”, R
DE LO CONTRARIO SI d <0 ENTONCES
ESCRIBA "no existe una raíz real"
TERMINARA SI
FIN
Desafío 5:
INICIO
numero =1
MIENTRAS (número * número <100) HACER
ESCRIBIR número, » «, número*número
número = número + 1
FINTANTQUE
FIN
Ejercicio 5
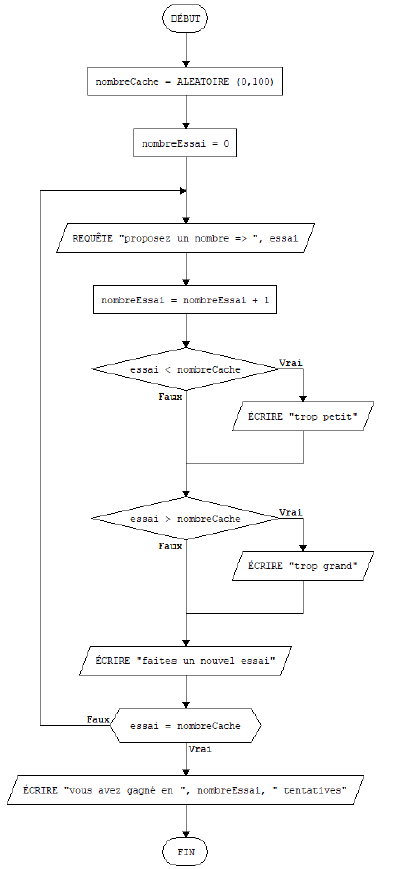
La computadora elige un número misterioso entre 1 y 100. Y tendrás que encontrarlo.
Para permitir que la computadora tenga un número aleatorio entre dos valores enteros y así realizar una respuesta sugerida, puedes utilizar la siguiente función:
número = ALEATORIO (p, q) para obtener un número aleatorio en el intervalo [p, q]
Establezca el diagrama de flujo o el pseudocódigo (o ambos…) de un algoritmo que permita a la computadora responder a sus propuestas numéricas.
Mensaje "demasiado pequeño" si su número es menor que el número misterioso
Mensaje "demasiado grande" si su número es mayor que el número misterioso
Mensaje "ganado" si su número es el número misterioso
Pon a prueba tus algoritmos.
Ejercicio 6
Desafío 1: Escribe el organigrama de un programa que
- Solicitar notas (se desconoce el número de notas)
- Guárdalos en un recipiente
El programa deja de pedir valoraciones cuando recibe una valoración negativa.
Después
- Calcula la media de las notas.
- Muestra el número de notas ingresadas y el promedio de estas notas.
Escriba el diagrama de flujo, pruébelo y luego tradúzcalo a pseudocódigo.
Desafío 2: Para obtener valores enteros aleatorios utilice la función RANDOM (p) que proporciona un número entero aleatorio en el intervalo ]0, p].
Valor = ALEATORIO (p)
Una vez lleno el contenedor, el programa mostrará el contenido del contenedor: posición y valor
Desafío 3: Escribe un programa en pseudocódigo que
- Llena un contenedor con valores aleatorios (ver desafío 2)
- Encuentra el valor más pequeño en el contenedor.
- Muestra el mensaje “el valor más pequeño es” y el valor encontrado
Desafío 4: ¡Escribe el algoritmo para calcular el factorial n! Elige la representación de tu preferencia y prueba tu algoritmo con valores variados (1, 3.6, 12, 0,-4)
Desafío 5: MCD de a y b según el algoritmo de Euclides
- Pregunta por los dos números a y b
- Realice la división euclidiana de a por b; observamos el resultado de esta división
- a toma el valor de b y b toma el valor de r
- empezamos de nuevo en 2
- cuando la decisión da un resto igual a 0, el PGCD es el último resto distinto de cero
- Luego muestre el PGCD
Escribe tu algoritmo y pruébalo para varios pares de valores (a,b)
Pregunta: ¿qué pasa si el resto de una división es 1?
Corrige y adapta tu algoritmo para tener en cuenta este caso.
Desafío 6: Verificando la conjetura de Siracusa
- toma un numero entero
- Si este número es par, divídelo por 2.
- Si este número es impar, toma el triple y suma 1
- Obtenemos un nuevo número entero y comenzamos de nuevo en 2.
Al final siempre obtenemos 1.
Escriba este algoritmo y obtenga que al final (cuando obtengamos 1) muestre el número de iteraciones realizadas.
Desafío 7: Calcular encuadrando un valor aproximado a 10-6 de la proporción áurea. Usando la fórmula: El valor entre dos valores sucesivos del cálculo de la proporción áurea debe ser menor que 10
Desafío 9: Compruebe si un número entero solicitado por el algoritmo es primo o no. El algoritmo debe responder: el número es primo o el número no es primo. Una pista: un número n es primo si tiene exactamente 2 divisores en el intervalo [1, n]
Desafío 10: Compruebe si un número entero solicitado por el algoritmo es primo o no. El algoritmo debe responder: el número es primo o el número no es primo. La misma pregunta pero encuentre otro enfoque para otro algoritmo. Una pista: un número n es primo si existe un divisor para este número en el intervalo ]1, n[
Desafío 11: reflexión sobre los algoritmos de números primos
¿Cuál de estos dos algoritmos crees que es más eficiente y por qué?
Desafío 4:
ENTRAR sustantivo, masculino—
hecho = 1
SI (n!=0) ENTONCES
PARA contador = 1 HASTA n HACER
facto = facto*contador
FINFOR
DE LO CONTRARIO
hecho = 1
TERMINARA SI
Hecho de retorno
Desafío 5:

Desafío 6:
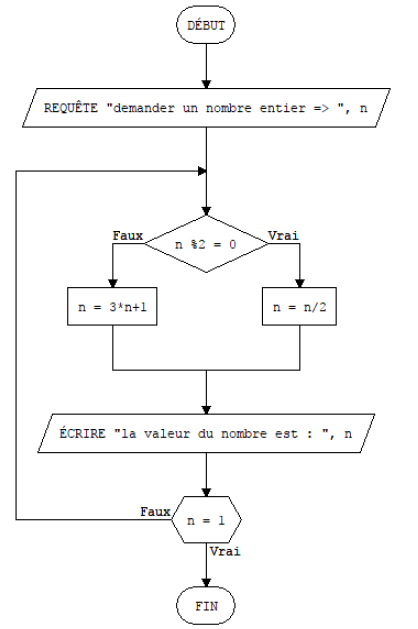
Desafío 9:
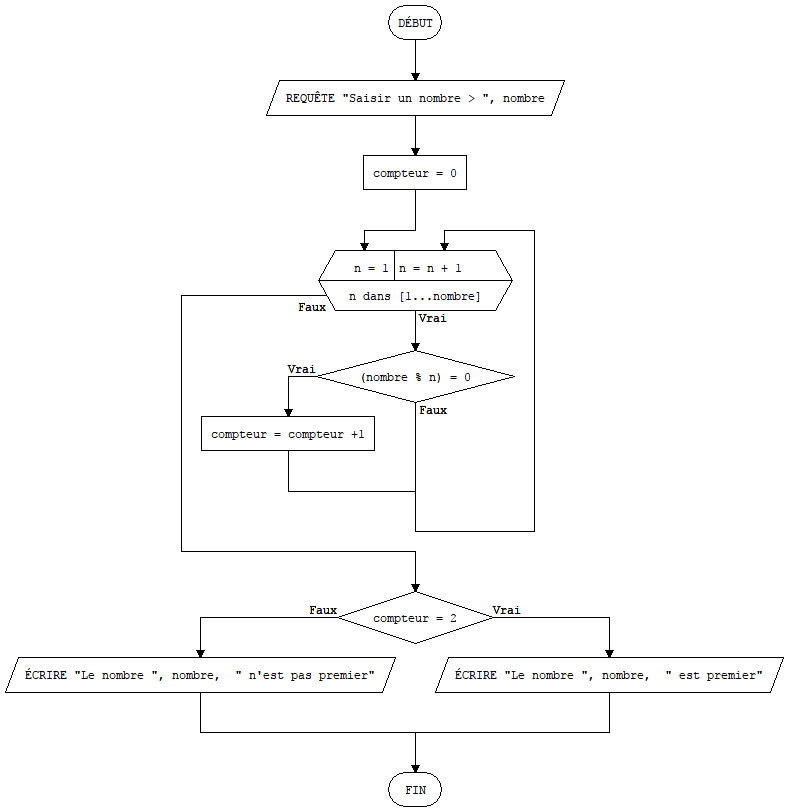
Desafío 10:
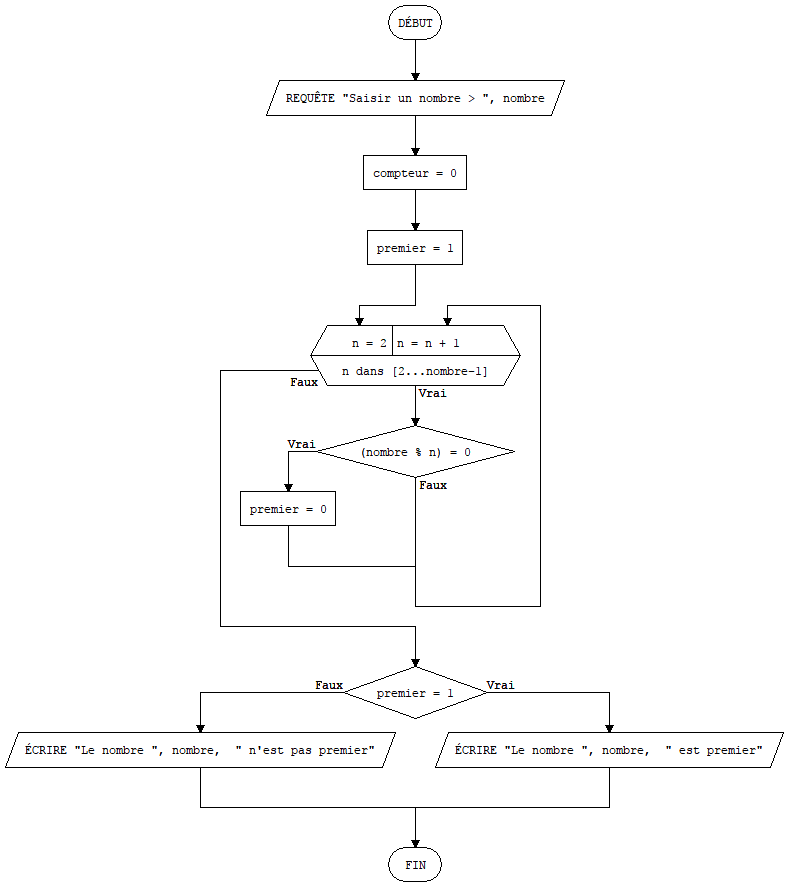
Ejercicio 7
Un estudio realizado por un instituto electoral así lo demostró desde 2001.
5% los miembros del partido A abandonan ese partido para ir al partido B.
8% los miembros del partido B abandonan este partido para ir al partido A.
En 2001, el partido A tenía 40.000 miembros y el partido B tenía 70.000.
Establecer el diagrama de flujo de un algoritmo que permitirá determinar en qué año el número de miembros del partido B superará al del partido A.
Ejercicio 8
Desafío 1: Establecer el diagrama de flujo de un algoritmo que requiere coordenadas polares y convierte a coordenadas cartesianas. Nos limitaremos a las coordenadas del plano, pero si eso te tienta,... ¿por qué no en 3D?
Desafío 2: Establecer el diagrama de flujo de un algoritmo que requiere coordenadas cartesianas y convierte a coordenadas polares. Lo mismo para 3D.
Desafío 3: Escribe el organigrama de un programa que
Pregunte qué tipo de conversión desea realizar (P a C o C a P)
Ejecute el diagrama de flujo para el desafío 1 o u2 según la respuesta a la pregunta inicial.
Desafío 4: Completa el diagrama de flujo anterior para que la ejecución del algoritmo pregunte luego de realizada la conversión, si desea comenzar de nuevo y comienza de nuevo siempre y cuando la respuesta sea sí.
Desafío 5: En aritmética, un número perfecto es un número natural. no tal que σ(no) = 2no donde σ(no) es la suma de los divisores positivos de no. Esto equivale a decir que un número natural es perfecto si es igual a la mitad de la suma de sus divisores o incluso a la suma de sus divisores estrictos. Entonces 6 es un número perfecto porque 2 × 6 = 12 = 1 + 2 + 3 + 6, o 6 = 1 + 2 + 3
Escribe el organigrama de un programa que
Encuentra y muestra números primos a partir del 1 inclusive.
Para información :
Hay 4 números perfectos entre (1 y 10.000) conocidos desde la antigüedad (Euclides)
Entonces: 33.550.336, entonces…. 2 305 843 008 139 952 128 (descubierto por Leonhard Euler), luego otros. En total hoy 49 incluyendo el último descubierto en enero de 2016.
Desafío 6: Escribir pseudocódigo, un programa que
Realiza la suma de números enteros: ∑ n para n igual a 1 hasta + ∞
Muestra para cada valor de n el valor de la suma obtenida
Pruebe su programa para obtener el valor de n más grande posible. La capacidad de procesamiento de tu computadora debería limitarte.
Evalúe el límite de esta suma para n que tiende a + ∞ y verifique la sumatoria de Ramanujan:
1 + 2 + 3 + 4 + 5 +…..hasta el infinito = -1/12.
Desafío 7: Escribe un algoritmo en pseudocódigo que
Cálculo de un valor aproximado de √150 a las 5th decimal (x n + 1-X no <10-5)
Usa la fórmula xn + 1 = (x no+a/x no)/2
Desafío 8: Escribe un algoritmo en pseudocódigo que
Solicita el valor de una inversión inicial y luego calcula y muestra el cambio de capital año tras año a razón de 3% por año.
La inversión inicial se realiza a principios de año (el 1ejem Enero)
La evaluación del capital y el pago de intereses se realiza al final del año (31 de diciembre)
Desafío 9: Escribe un algoritmo en pseudocódigo que
Determinar el último valor n de potencias de 2no como 2no <10.000
Desafío 5:

Lo que da el siguiente algoritmo:

Desafío 7:
INICIO
CONSULTA “valor de a=”, número
Uno = número
precisión = 0,00001
contador = 0
REPETIR
U = Uno
Uno = (U+número/U)/2.0
desviación = ABSOLUTA (Un-U)
contador = contador +1
HASTA (desviación < precisión)
ESCRIBA “la raíz de “,número” es “,REDONDEAR(Uno)
ESCRIBA “resultado obtenido en”, contador, “vueltas de bucle”
FIN
Desafío 8:
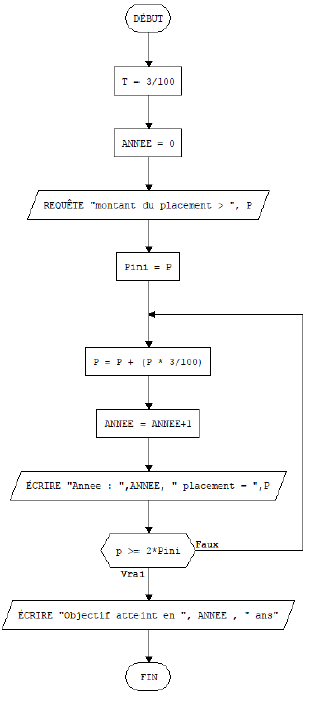
INICIO
T = 3/100
AÑO = 0
CONSULTA “monto de inversión > “, P
Pini = P
REPETIR
P = P + (P * 3/100)
AÑO = AÑO+1
ESCRIBA “Año: “,AÑO”, ubicación = “,P
HASTA p >= 2*Pini
ESCRIBA “Meta alcanzada en “, AÑO”, “años”
FIN
Ejercicio 9
Se distribuye un conjunto de cerillas (por ejemplo, 17), cada jugador retira de 1 a 3 cerillas por turno. El ganador es el que elimina el último partido (juego de Nim).
La estrategia ganadora es dejar a tu oponente con un número de partidos igual a 1 módulo 4.
Escribe el diagrama de flujo del algoritmo del juego en el que
- La computadora pregunta el número de partidos del juego.
- Hace jugar al jugador humano
- Da un turno quitando
- El número de coincidencias necesarias para dejar 1 módulo 4 si es posible.
- De lo contrario, un número aleatorio entre 1 y 3
- Y así sucesivamente hasta que solo quede un partido.
- Luego, el programa elige al ganador.
Para permitir que la computadora tenga un número aleatorio entre dos valores enteros y así realizar una respuesta sugerida, puedes utilizar la siguiente función:
número = ALEATORIO (p,q) para obtener un número aleatorio en el intervalo [p, q]
EN CONSTRUCCIÓN