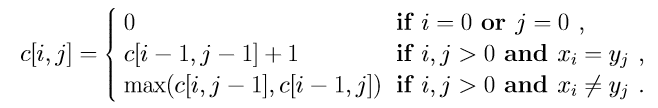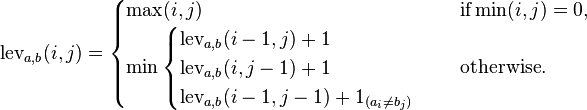Contenido
PalancaEjercicios corregidos de programación dinámica
Esta página ofrece varios ejercicios corregidos para programación dinámica y divide y vencerás. El objetivo es comprender la diferencia entre el paradigma Divide & Conquer y la programación dinámica. Los detalles de la búsqueda de ruta (camino más corto), problema de planificación, el problema del caudal máximo y, más en general, el Teoría de grafos se trata por separado.

Ejercicio 1
Escriba un pseudocódigo para un algoritmo de divide y vencerás para encontrar la posición del elemento más grande en una matriz de números. Escribe un pseudocódigo para un algoritmo de fuerza bruta, compara con el anterior. Mostrar un árbol del proceso del algoritmo divide y vencerás. ¿Cuál es el nivel máximo de árbol para los números?

El algoritmo de fuerza bruta es trivial: un bucle.
En cada nivel l, el árbol binario completo se compone de 2^(l-1) hojas. Entonces el total de los vértices es 2^l -1. Sea l el nivel del árbol, entonces l=sup(log_2 (n)).
Ejercicio 2
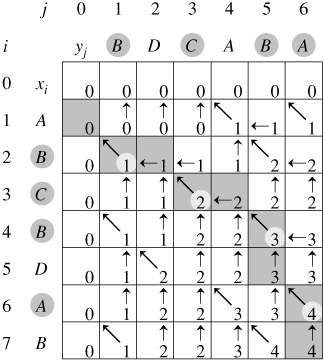
Suponga que su matriz de entrada se llama A. Lo que necesita hacer es formar otra matriz, digamos B, cada valor de i se calcula usando la fórmula recursiva, max(A[i], B[i- 1]+A[i ])
Lo que realmente haces es elegir expandir la ventana anterior o comenzar una nueva. Puede hacer esto ya que se supone que solo debe seleccionar elementos continuos como parte de sus subconjuntos.
5, -6, 7, 12, -3, 0, -11, -6
La respuesta sería 19 (del subarreglo {7,12} )
Ejercicio 3
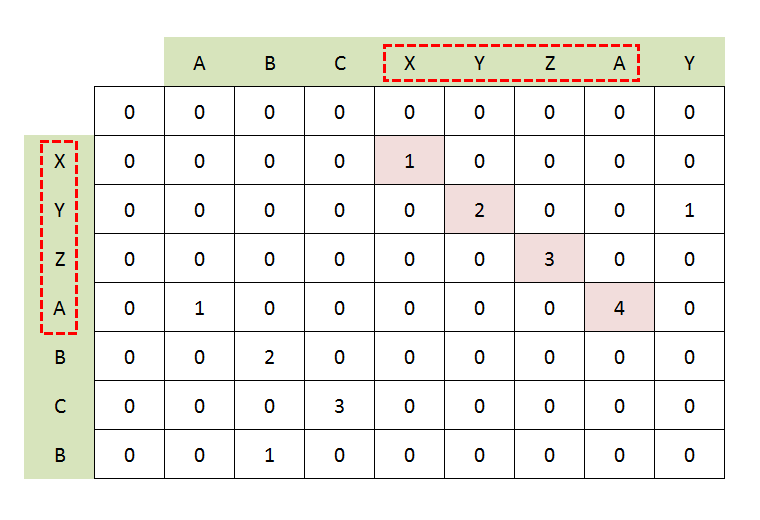
Utilice la subcadena común más larga para: BDCABA y ABCBDAB. El algoritmo se describe de la siguiente manera:

Ejercicio 4
Haga coincidir la subcadena común más larga con la subsecuencia común más larga: BDCABA y ABCBDAB. El problema de la subsecuencia común más larga (LCS) es encontrar la subsecuencia común más larga de todas las secuencias en un conjunto de secuencias (a menudo solo dos secuencias).
Esto difiere de los problemas comunes de búsqueda de subcadenas: a diferencia de las subcadenas, no se requiere que las subsecuencias ocupen posiciones consecutivas en las secuencias originales.
Ejercicio 5
La distancia de Levenshtein es una métrica de cadena para medir la diferencia entre dos secuencias. De manera informal, la distancia de Levenshtein entre dos palabras es el número mínimo de modificaciones de un solo carácter (es decir, inserciones, eliminaciones o sustituciones) necesarias para cambiar una palabra por otra. Proponga un programa dinámico para resolver este problema. Ensayo con MEILENSTEIN y LEVENSHTEIN.
Ejercicio 6
Alice y Bob se turnan para jugar un juego, con Alice comenzando primero.
Inicialmente, hay un número n en el tablero. En el turno de cada jugador, ese jugador hace un movimiento que consiste en:
Elija cualquier x con 0 < x < n y n % x == 0.
Reemplace el número n en la pizarra con n – x.
Además, si un jugador no puede moverse, pierde el juego.
Devuelve true si y solo si Alice gana el juego, asumiendo que ambos jugadores están jugando de manera óptima.
Ejemplo 1:
Entrada: n = 2
Salida: verdadero
Explicación: Alice elige 1 y Bob no tiene más movimientos.
Ejemplo 2:
Entrada: n = 3
Salida: falso
Explicación: Alice elige 1, Bob elige 1 y Alice no tiene más movimientos.
Para responder a este problema, construiremos una tabla de soluciones. dp[i] indica el resultado del juego para el número i dado y para el jugador que comenzó el juego. Alice probará todos los factores y elegirá el que le dé a su oponente un valor perdedor.

También es posible resolver este problema de una manera recursiva más clásica, llamada Top-Down.

Y para un lado más práctico, vamos a agregar una memorización.

Ejercicio 7
Se le proporciona una matriz de costos de enteros donde costo[i] es el costo del i-ésimo escalón de una escalera. Una vez que haya pagado el costo, puede subir uno o dos escalones.
Puede comenzar desde el paso con el índice 0 o desde el paso con el índice 1.
Devolver el coste mínimo para llegar a la parte superior del piso.
Ejemplo 1:
Entrada: costo = [10,15,20]
Salida: 15
Explicación: Comenzará en el índice 1.
– Paga 15 y sube dos escalones para llegar a la cima.
El costo total es de 15.
Ejemplo 2:
Entrada: costo = [1,100,1,1,1,100,1,1,100,1]
Salida: 6
Explicación: Comenzará en el índice 0.
– Paga 1 y sube dos escalones para llegar a la pista 2.
– Paga 1 y sube dos escalones para llegar a la pista 4.
– Paga 1 y sube dos escalones para llegar a la pista 6.
– Paga 1 y sube un escalón para llegar a la pista 7.
– Paga 1 y sube dos escalones para llegar a la pista 9.
– Paga 1 y sube un escalón para llegar a la cima.
El costo total es de 6.
Para un primer borrador, resolveremos este problema recursivo. Para ello tenemos en cuenta el menor coste al considerar que retrocedemos un paso y dos pasos. Y así hasta tener el costo del primer o segundo paso.
costo mínimo (0) = costo [0]costo mínimo (1) = costo [1]
mincost(i) = cost[i]+min(mincost(i-1), mincost(i-2))
Lo que da el siguiente código:

En un segundo paso, nos mantendremos en un enfoque de arriba hacia abajo y agregaremos un sistema de memorización. Por lo tanto, un minCost ya encontrado no se volverá a calcular más tarde.

Finalmente, tomaremos el problema de abajo hacia arriba para hacer programación dinámica;

Ejercicio 8
Alice y Bob están jugando con montones de rocas. Hay un número par de pilas dispuestas en una fila, y cada pila tiene un número entero positivo de pilas de piedras[i].
El objetivo del juego es terminar con la mayor cantidad de piedras. El número total de piedras en todas las pilas es impar, por lo que no hay empate.
Alice y Bob se turnan, Alice comienza primero. Cada turno, un jugador toma toda la pila de piedras desde el principio o desde el final de la fila. Esto continúa hasta que no quedan más montones, momento en el que gana la persona con más piedras.
Suponiendo que Alice y Bob están jugando de manera óptima, devuelva true si Alice gana el juego o false si Bob gana.
Entrada: piedras = [5,3,4,5]
Salida: verdadero
Alice comienza primero y solo puede tomar los primeros 5 o los últimos 5.
Digamos que toma los primeros 5, por lo que la línea se convierte en [3, 4, 5].
Si Bob toma 3, entonces el tablero es [4, 5] y Alice toma 5 para ganar con 10 puntos.
Si Bob toma los últimos 5, entonces el tablero es [3, 4] y Alice toma 4 para ganar con 9 puntos.
Esto demostró que tomar el top 5 fue un movimiento ganador para Alice, por lo que devolvemos verdadero.
Comencemos con un enfoque de arriba hacia abajo con memorización.
- Tenga en cuenta que ambos jugadores juegan de manera óptima, por lo que jugamos de manera óptima sin importar quién es Alice, quién es Bob.
- Deje que dp (izquierda, derecha) devuelva [firstScore, secondScore] donde firstScore es la puntuación máxima cuando el jugador 1 juega primero, secondScore es la puntuación máxima cuando el jugador 2 juega segundo, recoge piedras en montones [left]... piles [right].
- Para piedras en montones [izquierda]... montones [derecha], hay 2 opciones para que el jugador 1 elija:
- Elija a la izquierda: pickLeft = dp (izquierda + 1, derecha).
- Puntuación del jugador 1 = pilas [izquierda] + puntuación de segunda elección de pickLeft, por lo que firstScore = pilas [izquierda] + pickLeft [1]
- Puntuación del jugador 2 = puntuación de la primera elección de pickLeft, por lo que secondScore = pickLeft[0]
- Elegir a la derecha: elegirDerecha = dp(izquierda, derecha – 1).
- Puntuación del jugador 1 = pilas [derecha] + segunda puntuación de pickRight, por lo que firstScore = pilas [derecha] + pickRight [1]
- Puntuación del jugador 2 = puntuación de la primera elección de pickRight, por lo que secondScore = pickRight[0].
- Elija a la izquierda: pickLeft = dp (izquierda + 1, derecha).
- Necesitamos obtener la puntuación máxima cuando el jugador 1 juega primero entre más de 2 opciones.
- Finalmente, dp(0, len(stacks) – 1) devuelve [firstScore, secondScore], donde alexScore = firstScore ya que Alice juega primero, leeScore = secondScore ya que Bob juega segundo.

Ahora vamos a hacer un algoritmo de abajo hacia arriba mientras mantenemos la memorización. Así el algoritmo estará en programación dinámica.

Ejercicio 9
Hay soldados haciendo fila. A cada soldado se le asigna un valor de rango único.
Debes formar un equipo de 3 soldados entre ellos según las siguientes reglas:
Elija 3 soldados con índice (i, j, k) con calificación (calificación [i], calificación [j], calificación [k]).
Un equipo es válido si: (puntuación[i] <puntuación[j] <puntuación[k]) o (puntuación[i] >puntuación[j] >puntuación[k]) donde (0 <= i < j < k < no).
Devuelve el número de equipos que puedes formar dadas las condiciones. (los soldados pueden formar parte de varios equipos).
Ejemplo 1:
Entrada: puntuación = [2,5,3,4,1]
Salida: 3
Explicación: Se pueden formar tres equipos dependiendo de las condiciones. (2,3,4), (5,4,1), (5,3,1).
Ejemplo 2:
Entrada: puntuación = [2,1,3]
Salida: 0
Explicación: No podemos formar ningún equipo dadas las condiciones.
Es fácil hacer un algoritmo codicioso. Este último está en O (n ^ 3), por lo que intentaremos mejorar el complejidad con programación dinámica.

Aquí está la idea principal en la versión de programación dinámica:
Primero, calculamos este caso score[i] > score[j] > score[k] dado que i > j > k. A continuación, calcule la puntuación del caso [i] < puntuación [j] < puntuación [k].
Establecer dp[i]: cuántos elementos en la notación de 0 a i-1 son menores que la notación[i].
Por cada vez que encontramos nota[i] > nota[j], acumulamos dp[j]. Aquí, dp[j] significa cuántas notas[k] existen desde 0 hasta j-1. Es decir, cuántos casos satisfacen grado[i] > grado[j] > grado[k].

Ejercicio 10
Se le proporciona un gráfico de precios donde el precio[i] es el precio de una acción dada en el i-ésimo día y una tarifa entera que representa las tarifas de transacción.
Encuentre la ganancia máxima que puede obtener. Puede realizar tantas transacciones como desee, pero debe pagar tarifas de transacción por cada transacción.
Nota: no puede participar en múltiples transacciones simultáneamente (es decir, debe vender las acciones antes de volver a comprar).
Entrada: precio = [1,3,2,8,4,9], tarifa = 2
Salida: 8
Explicación: La ganancia máxima se puede lograr mediante:
– Comprar a precios [0] = 1
– Vender a precios[3] = 8
– Comprar a precios [4] = 4
– Vender a precios[5] = 9
La ganancia total es ((8 – 1) – 2) + ((9 – 4) – 2) = 8.
Comencemos primero con el enfoque de arriba hacia abajo.
- Sea dp(i, canBuy) la ganancia máxima que podemos obtener del precio[i..n-1] con el indicador canBuy == True significa que podemos comprar el i-ésimo día.
- Para el iésimo día tenemos 2 opciones:
- Ignóralo: beneficio = dp(i+1)
- Cómpralo o véndelo
- Si compra: beneficio = dp(i+1) – precio[i]
- Si venta: beneficio = dp(i+1) + precio[i] – comisión

Pasaremos a un enfoque de abajo hacia arriba para hacer una programación dinámica más tradicional.
Sea dp[i][j] el beneficio máximo que podemos obtener del precio[i..n-1] con bandera j == 1 significa que podemos comprar en el i-ésimo día.

Dado que nuestro dp solo accede a 2 estados: el estado actual de dp dp, el estado anterior de dp dpPrev. Podemos optimizar a O(1) en complejidad espacial.

Ejercicio 11
Planeaste un viaje en tren con un año de anticipación. Los días del año en los que viajará se dan como un número entero de días. Cada día es un número entero entre 1 y 365.
Los billetes de tren se venden de tres formas diferentes:
un pase de 1 día se vende al precio de [0] dólares,
un pase de 7 días se vende por un costo de [1] dólares, y
un pase de 30 días cuesta [2] dólares.
Los pases permiten tantos días de viaje consecutivos como sea posible.
Por ejemplo, si conseguimos un pase de 7 días el día 2, podemos viajar durante 7 días: 2, 3, 4, 5, 6, 7 y 8.
Devuelva la cantidad mínima de dólares que necesita para viajar cada día en la lista de días dada.
Entrada: días = [1,4,6,7,8,20], costos = [2,7,15]
Salida: 11
Por ejemplo, aquí tienes una forma de comprar pases que te permitan viajar de acuerdo a tu plan de viaje:
El día 1, compró un pase de 1 día por un costo[0] = 2 $, que cubría el día 1.
El día 3, compró un pase de 7 días por un costo[1] = 7 $, que cubría los días 3, 4, …, 9.
El día 20, compró un pase de un día por un costo[0] = 2 $, que cubría el día 20.
En total has gastado 11 $ y cubierto todos los días de tu viaje.
Veremos aquí el enfoque de abajo hacia arriba porque el razonamiento es muy similar al problema de mochila (mochila) en la construcción de la solución.
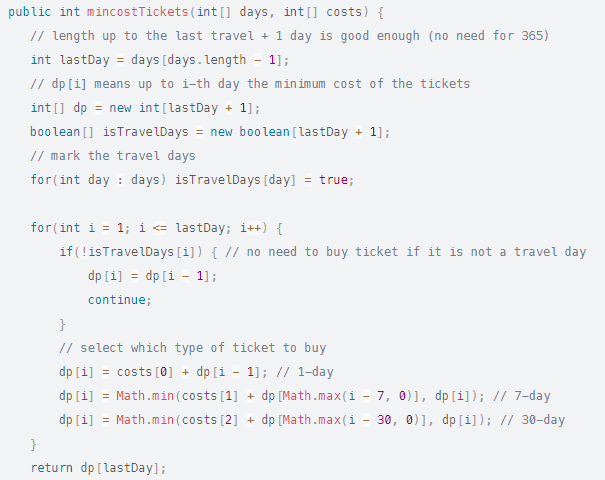
dp[i] significa hasta el día th el costo mínimo de los boletos. El tamaño de la matriz dp depende del último día de viaje, por lo que no necesitamos una longitud de matriz de 365.
Necesitamos una matriz booleana para marcar los días de viaje, la razón es que si no es un día de viaje, no necesitamos un boleto. Sin embargo, si es un día de viaje, consideramos tres escenarios (con tres tipos de boletos):
Si un billete de 1 día el día i, dp[i] = dp[i – 1] + coste[0]
Si un billete de 7 días finaliza el día i, dp[i] = min(dp[i – 7], dp[i – 6] … dp[i – 1]) + coste[1]
Si un billete de 30 días finaliza el día i, dp[i] = min(dp[i – 30], dp[i – 29] … dp[i – 1]) + coste[2]
Pero dado que el valor de la matriz dp aumenta, entonces:
Para un boleto de 7 días que finaliza el día i, dp[i] = dp[i – 7] + cost[1]
Para un boleto de 30 días que finaliza el día i, dp[i] = dp[i – 30] + cost[2]
Ejercicio 12
Se le proporciona una matriz de valores enteros donde valores[i] representa el valor del i-ésimo sitio turístico. Dos sitios turísticos i y j tienen una distancia j – i entre ellos.
La puntuación de un par (i < j) de sitios turísticos es valores[i] + valores[j] + i – j: la suma de los valores de los sitios turísticos, menos la distancia entre ellos.
Devuelve la puntuación máxima de un par de miras.
Entrada: valores = [8,1,5,2,6]
Salida: 11
Tenemos i = 0, j = 2, valores[i] + valores[j] + i – j = 8 + 5 + 0 – 2 = 11
Supongamos que elegimos el sitio [i,…j]. La partitura se puede dividir en 2 partes.
La primera parte es el startGain que ganas al comenzar en un cierto punto i. Tenga en cuenta que startGain[i] = a[i] + i.
La segunda parte es endGain, que es la cantidad que ganas al terminar en cierto punto j. Tenga en cuenta que endGain[i] = a[j] – j.
Tenga en cuenta que endGain puede ser negativo.
La ganancia general para [i,…j] no es más que startGain[i] + endGain[j]. (Esto puede ser fácilmente verificado por las definiciones).
Debemos maximizar la ganancia total.
¿Cuáles son las posiciones posibles para iniciar el viaje? Está claro que podemos empezar todo menos el último elemento. Por lo tanto, el viaje óptimo debe comenzar en uno de estos elementos.
Supongamos que solo se nos permite iniciar un viaje en i. ¿Cuál es la cantidad máxima que podemos ganar en este caso? Bueno, dado que startGain es fijo, necesitamos maximizar endGain. Podemos hacer esto deteniéndonos en un elemento que tenga la ganancia final máxima siempre que aparezca a la derecha de i.
Como se muestra arriba, para cada i necesitamos encontrar la ganancia final máxima a su derecha.
maxEndRight[i] = max(maxEndRight[i+1], endGain[i+1]) = max(maxEndRight[i+1], a[i+1] – (i+1))
maxEndRight[i] representa la ganancia final más alta que puede obtener deteniéndose en cualquier punto estrictamente a la derecha de i. Como por definición ya conocemos endGain[i+1] (la mayor ganancia posible al terminar en cualquier punto a la derecha de i+1), solo tenemos que comprobar la posibilidad de saber si s detenerse en i+1 sería beneficioso O no. De ahí la definición de DP.
Para cada i válida, gananciageneral[i] = gananciainicial[i] + maxEndRight[i] = a[i] + i + maxEndRight[i]
Tenga en cuenta que maxEndRight[i] solo depende de maxEndRight[i+1]. Por lo tanto, podemos usar 2 variables para rastrear valores anteriores.
Dado que necesitamos el valor de maxEndRight[i+1] para calcular el valor de maxEndRight[i], comenzamos las iteraciones desde atrás.
Como se indicó, los viajes no pueden comenzar en el último elemento, por lo que el ciclo for comienza en i=n-2. Para este valor, maxEndingRight se inicializa en endGain[lastIndex] porque esa es la única forma posible de finalizar el viaje.

Ejercicio 13
Eres un ladrón profesional que planea robar casas a lo largo de una calle. Cada casa tiene una cierta cantidad de dinero escondida, la única restricción que le impide robar en cada una de ellas es que las casas adyacentes tienen sistemas de seguridad conectados y automáticamente contactará a la policía si dos casas adyacentes fueron robadas en la misma noche.
Dada una serie de números enteros que representan la cantidad de dinero en cada casa, devuelve la cantidad máxima de dinero que puedas robar esta noche sin alertar a la policía.
Entrada: números = [1,2,3,1]
Salida: 4
Explicación: Roba la casa 1 (dinero = 1) y luego roba la casa 3 (dinero = 3).
Cantidad total que puedes robar = 1 + 3 = 4.
Entrada: números = [2,7,9,3,1]
Salida: 12
Explicación: robar casa 1 (dinero = 2), robar casa 3 (dinero = 9) y robar casa 5 (dinero = 1).
Cantidad total que puedes robar = 2 + 9 + 1 = 12.
Encontremos una relación recursiva.
Un ladrón tiene 2 opciones: a) robar la casa actual i; b) no robar la casa actual.
Si se selecciona una opción 'a', eso significa que no puede robar la casa i-1 anterior, pero puede cambiar de forma segura a la anterior a la i-2 anterior y obtener todo el botín acumulativo que sigue.
Si se selecciona la opción "b", el ladrón obtiene todo el botín posible del robo de i-1 y todos los edificios posteriores.
Por lo tanto, se trata de calcular qué es lo más rentable:
robo de la casa actual + botín de las casas anteriores a la anterior el botín del robo de la casa anterior y cualquier botín capturado antes de ese
robar(i) = Math.max( robar(i – 2) + valor actual de la casa, robar(i – 1) )
Esto daría la siguiente versión recursiva:

Ahora pensemos en un método usando memorización. Para esto, vamos a considerar que al agregar cada casa (así en la etapa i, o no robamos esta casa (por lo tanto, el mismo valor que la etapa i-1), o robamos la casa y, por lo tanto, potencialmente eso en i-2 .
Por tanto, tomamos el máximo entre el óptimo en la etapa i-1 y en i-2 + valor de la nueva casa. Como recordatorio, cada paso es óptimo porque resolver el problema sin la nueva casa es óptimo por el principio del subproblema.
que dan:

Estamos aquí en una complejidad en la memoria y en el tiempo en O(n).
Transformemos este código de abajo hacia arriba, por lo que en programación dinámica:
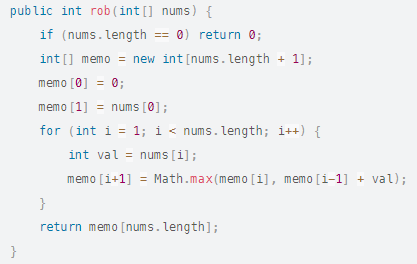
Tenga en cuenta que, al igual que Fibonacci, no necesitamos mantener el conjunto de valores anteriores porque el subproblema óptimo en i-1 e i-2 no cambia sea cual sea la nueva casa. ¡Tenga en cuenta que esta optimización no le permitirá saber qué casas se han elegido!

La complejidad del espacio es O(1).
Ejercicio 14
Te dan k huevos idénticos y tienes acceso a un edificio de n pisos numerados del 1 al n.
Usted sabe que hay un piso f donde 0 <= f <= n tal que cualquier huevo que caiga en un piso más alto que f se romperá, y cualquier huevo que caiga en o debajo del piso f no se romperá.
Con cada movimiento, puedes recoger un huevo intacto y dejarlo caer desde cualquier piso x (donde 1 <= x <= n). Si el huevo se rompe, ya no puedes usarlo. Sin embargo, si el huevo no se rompe, puedes reutilizarlo en futuros movimientos.
Devuelve el número mínimo de movimientos que necesita para determinar con certeza cuál es el valor de f.
Entrada: k = 1, n = 2
Salida: 2
Suelta el huevo del nivel 1. Si se rompe, sabemos que f = 0.
De lo contrario, suelta el huevo del nivel 2. Si se rompe, sabemos que f = 1.
Si no se rompe, entonces sabemos que f = 2.
Por lo tanto, necesitamos al menos 2 movimientos para determinar con certeza cuál es el valor de f.
Primero, podemos ver que para obtener la respuesta de pisos y huevos más grandes, los resultados de casos más pequeños son útiles para el análisis, lo que lleva a la programación dinámica.
Entonces, ¿cómo definir un estado para cada gota para obtener el piso óptimo? Aquí tenemos dos variables:
El número de huevos que quedan por descartar i, (0 <= i <= K)
El número de pisos que quedan para probar j, (1 <= j <= N)
La respuesta (los tiempos más pequeños para obtener el piso óptimo) puede ser el valor de cada estado dp.
El caso base es bastante intuitivo de encontrar. Considere los casos con huevos y pisos más pequeños:
dp[1][j] = j, j = 1…N # un huevo, revisa cada piso del 1 al j
dp[i][0] = 0, i = 1…K # sin piso, sin caída necesaria para obtener el piso óptimo
dp[i][1] = 1, i = 1…K # una etapa, verificar solo una vez
Para obtener una relación recursiva, considere un caso de prueba: 3 huevos y 100 pisos.
Para la próxima caída, puedo elegir una etapa del 1 al 100, digamos que elijo 25.
Hay 2 resultados posibles para esta gota:
el huevo se rompió, ahora tengo 2 huevos y el piso para elegir se convierte en 1~24.
el huevo sigue siendo seguro, todavía tengo 3 huevos y el piso para elegir se convierte en 26~100.
Pensando en el peor de los casos y usando la definición de dp anterior, podemos describir la situación de obtener el piso óptimo eligiendo el piso 25 para la próxima caída como:
dp[3][100] = 1 + máx(dp[2][24], dp[3][75])
Además del piso 25, en términos de próximo descenso, también podemos elegir el piso del 1 al 100.
Cada gota sería similar al caso de la 25 anterior. El resultado final sería el mínimo de todas las opciones posibles de los siguientes pisos para colocar:
dp[3][100] = mín(…, 1 + máx(dp[2][23], dp[3][76]), 1 + máx(dp[2][24], dp[3][ 75]), 1 + max(dp[2][25], dp[3][74]), …) (tome el piso 24, 25, 26 como ejemplo)
Para generalizar el ejemplo anterior, la fórmula dp sería:
dp[i][j] = min(1 + max(dp[i-1][k-1], dp[i][jk])), k = 1.2,…j
Por lo tanto, definimos dp[i][j] como el menor número de gotas para obtener el piso óptimo con i huevos y j pisos restantes.
Aquí hay una primera solución de fuerza bruta en O (kn ^ 2)

Sin embargo, esta idea es muy de fuerza bruta, porque compruebas todas las posibilidades.
Así que miro este problema de una manera diferente:
dp[M][K] significa que, dados K huevos y M movimientos, ¿cuál es el número máximo de pisos que podemos verificar?
La ecuación de dp es: dp[m][k] = dp[m – 1][k – 1] + dp[m – 1][k] + 1,
lo que significa que llevamos 1 movimiento a un piso, si el huevo se rompe, entonces podemos comprobar dp[m – 1][k – 1] pisos. si el huevo no se rompe, podemos verificar las etapas dp[m – 1][k].
Lo que daría el siguiente código:

¡No pruebes este código, tendrás un TLE! ¡Debería optimizarse con un árbol binario que haremos en otro curso!
Ejercicio 15
Los demonios capturaron a la princesa y la encarcelaron en la esquina inferior derecha de un calabozo. La mazmorra consta de mxn habitaciones dispuestas en una cuadrícula 2D. Nuestro valiente caballero se encuentra inicialmente en la habitación superior izquierda y debe abrirse camino a través de la mazmorra para salvar a la princesa.
El caballero tiene un número inicial de puntos de vida representados por un número entero positivo. Si en algún momento sus puntos de vida caen a 0 o menos, muere inmediatamente.
Algunas habitaciones están custodiadas por demonios (representados por números enteros negativos), por lo que el caballero pierde salud al entrar en estas habitaciones; otras habitaciones están vacías (representadas por 0) o contienen orbes mágicos que aumentan la salud del caballero (representados por números enteros positivos).
Para llegar a la princesa lo más rápido posible, el caballero decide moverse solo hacia la derecha o hacia abajo con cada paso.
Dale al caballero un mínimo de salud inicial para que pueda salvar a la princesa.
Tenga en cuenta que cualquier habitación puede contener amenazas o potenciadores, incluso la primera habitación en la que entra el caballero y la habitación inferior derecha donde está encarcelada la princesa.
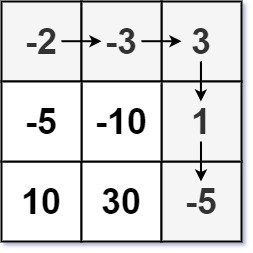
Entrada: mazmorra = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
Salida: 7
Explicación: La salud inicial del caballero debe ser de al menos 7 si sigue el camino óptimo: DERECHA -> DERECHA -> ABAJO -> ABAJO.
Probablemente cuando vea este problema y tenga algo de experiencia en este tipo de problemas, pueda adivinar que se trata de un problema de programación dinámica. Sin embargo, incluso si entiendes esto, no es fácil resolverlo. Usemos dp de arriba hacia abajo, es decir, sea dp[i][j] los hp mínimos que necesitamos para alcanzar a la princesa si comenzamos desde el punto (i,j). Considere el siguiente ejemplo:
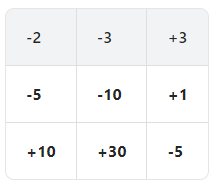
Agreguemos una fila ficticia en la parte inferior y una columna ficticia a la derecha para manejar más fácilmente los casos límite. Lo llenamos con infinito, excepto dos: vecinos de nuestra princesa. Lo explicaré un poco más tarde.
¿Cómo evaluar dp[i][j]? Necesitamos examinar dos celdas: dp[i+1][j] y dp[i][j+1] y evaluar dos posibles candidatos: dp[i+1][j]-dungeon[i][j] y dp [i][j+1]-mazmorra[i][j].
- Si al menos uno de estos dos números es negativo, significa que uno puede sobrevivir con solo 1 hp: (mira el número +30 en nuestra tabla, por ejemplo)
- Si estos dos números son positivos, debemos tomar el mínimo, vea por ejemplo el número -10 en nuestra tabla: para sobrevivir necesitamos 5- -10 = 15 si vamos a la derecha y 1- -10 = 11 si vamos baja, por supuesto elegimos 11.
Estas condiciones se pueden escribir en una ecuación: dp[i][j] = max(min(dp[i+1][j],dp[i][j+1])-dungeon[i][j], 1).
Finalmente, ¿por qué puse de 1 a 2 princesas vecinas? Para que esta fórmula sea válida para la celda princesa: si tenemos un número negativo como -5 en esta celda, necesitamos 6 mo para sobrevivir, si tenemos un número no negativo en esta celda, necesitamos 1 mo para sobrevivir.
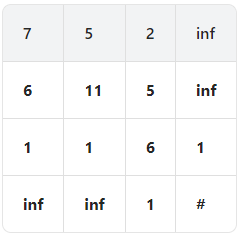
La complejidad de espacio y tiempo es O(nm)

También es posible hacerlo con dp descendente, pero en ese caso tienes que usar la búsqueda binaria, porque no sabes de antemano si estás sobreviviendo de x HP o no. La complejidad será O(nm log(MAX_HP)) en este caso.
Ejercicio 16
Se le proporciona una cuadrícula de matriz de filas x columnas que representa un campo de cerezas donde la cuadrícula [i] [j] representa la cantidad de cerezas que puede recolectar de la celda (i, j).
Tienes dos robots que pueden recoger cerezas por ti:
El robot #1 se encuentra en la esquina superior izquierda (0, 0) y
El robot #2 se encuentra en la esquina superior derecha (0, cols – 1).
Devuelva la cantidad máxima de cerezas recolectadas usando ambos bots siguiendo las reglas a continuación:
Desde una celda (i, j), los robots pueden moverse a la celda (i + 1, j – 1), (i + 1, j) o (i + 1, j + 1).
Cuando un robot pasa por una celda, recoge todas las cerezas y la celda se convierte en una celda vacía.
Cuando los dos robots se quedan en la misma celda, solo uno toma las cerezas.
Los dos robots no pueden abandonar la parrilla en ningún momento.
Ambos robots deben llegar a la fila inferior de la cuadrícula.
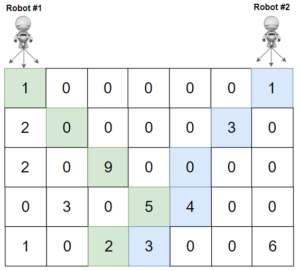
Entrada: cuadrícula = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0, 0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
Salida: 28
Explicación: Las trayectorias de los robots 1 y 2 se describen en verde y azul respectivamente.
Cerezas tomadas por el Robot #1, (1+9+5+2)=17.
Cerezas tomadas por el Robot #2, (1+3+4+3)=11.
Cerezas totales: 17 + 11 = 28.
En este problema, supondremos que ambos robots se moverán a la siguiente fila al mismo tiempo para que ambos permanezcan en la misma fila. Esta será la primera vista previa para resolver este problema.
Como se describe en el enunciado del problema, podemos movernos en 3 direcciones (i+1, j-1), (i+1, j) o (i+1, j+1). Todo en la siguiente fila pero con una columna diferente.
Dado que tenemos 3 direcciones para cada robot, en cada fila hay 9 (3 x 3) estados hacia los que podemos movernos. (3 estados para el primer robot y 3 estados para el segundo robot por lo que es 3 x 3).
Y como dice la sugerencia, necesitamos tener una matriz DP de 4 filas. Como se trata de una matriz tridimensional, habrá una matriz bidimensional que será n*n, es decir, no. de columna * no. de columna Donde la fila especificará la posición de la columna Robot1 y la columna especificará la posición de la columna Robot2.
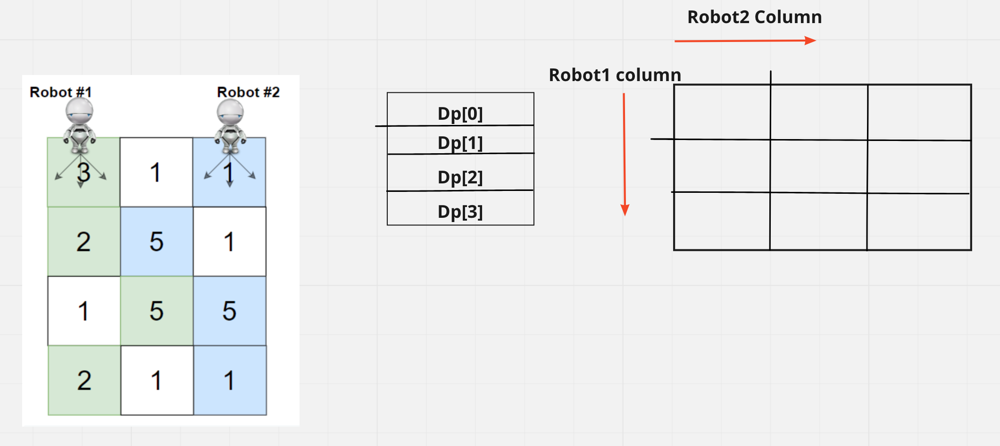
Inicialmente, sabemos que robot1 está en la posición 0 y robot2 está en la columna de posición - 1, que es la última columna.
Tenemos que llenar dp[0], es decir, la primera fila y en esta primera fila la posición de la columna para el robot será (0, 2) porque 0 significa la posición de la columna para el robot1 y 2 significa la posición de la columna para el robot2 en la cuadrícula.
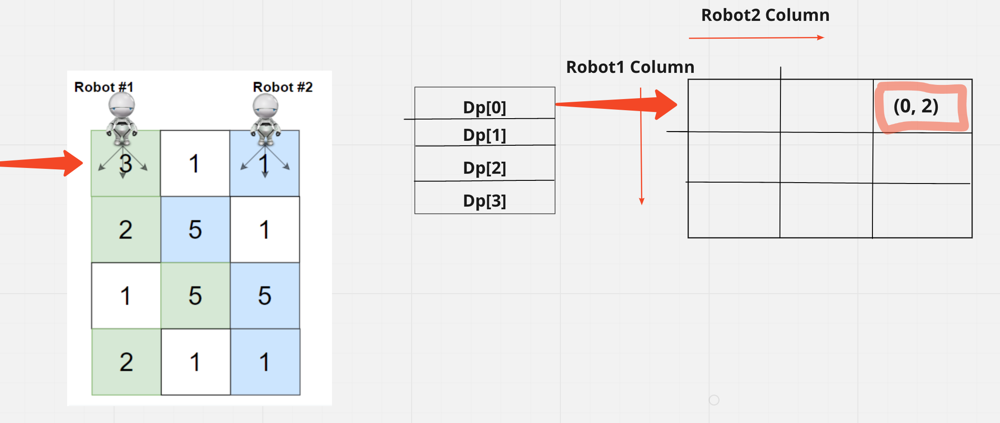
Cuando llenamos el espacio obtenemos el valor 3 + 1 que es 4
Ahora necesitamos llenar la segunda fila. Y en la 2ª línea también habrá una matriz n*m. Si tomamos la posición anterior de robot1 como 0, tenemos 3 columnas en las que puede ir en la siguiente fila, es decir, col {-1, 0, 1}. Como col1 está fuera de rango, descartamos este "-1" y mantenemos solo "0, 1"
Y el mismo robot2 está en 2, podemos llegar a la columna {1, 2, 3}. Como col3 está fuera de los límites, descartamos "3" y mantenemos solo "1, 2"
Ahora cuando creamos la combinación de todas las columnas que pueden ser robot1 y robot2 obtenemos 4 valores y cuando la llenemos será:
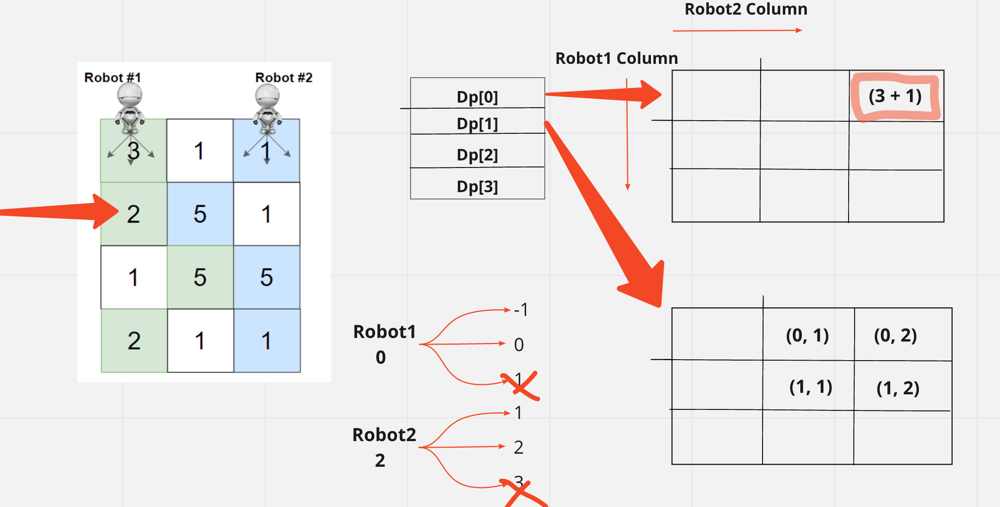
Así que si buscamos (0, 1) el valor que devuelve será grid[0][1] + grid[1][1] + anterior. Pero para (1,1) será grid[1][1] + anterior.
Si ahora hablamos de código. Tomemos dp[fila][columna][columna] nuestra programación dinámica. Al principio col1=0 y col2=columna-1 (ubicación del robot).
Tenemos la solución max=dp[0][col1][col2].
Aquí está el código para completar por cada valor creciente de dp[raw][][]
// ahora se separa donde necesitamos iterar sobre cada fila;
por(En t I = 1; I < fila; I++){ // cada fila comienza con 1
// En esta cada fila de dp, necesitamos eliminar nuestra lógica seleccionando esa columna en particular, como la posición inicial
// necesitamos hacer un bucle en todas las columnas precisas en esta fila
// como dije habrá n * m columna
por(En t c1 = 0; c1 < collar; c1++){
por(En t c2 = 0; c2 < collar; c2++){
// ahora de cada columna necesitamos llenar el cubo; para todas las combinaciones o toda la celda que podamos alcanzar; con respectivo robot1 y robot2
// ahora necesitamos primero tomar el valor anterior, que discutimos
En t anterior = doble penetración[I - 1][c1][c2];
tejo(anterior >= 0){ // si ese es el caso, necesitamos realizar nuestra operación, si es un valor -ve significa que aún no hemos llegado a esa celda en particular. Y encima es por eso que inicializamos toda la matriz con -1
// Ahora necesitamos iterar sobre todas las combinaciones de columnas en las que pueden estar c1 y c2. Para eso, definimos una matriz de dirección en la parte superior.
por(En t d1: dirección){ // para c1 tenemos la dirección "d1" y la iteramos
col1 = d1 + c1; // y la columna1 será d1 + c1
por(En t d2: dirección){ // para c2 tenemos la dirección "d2" y la iteramos
col2 = d2 + c2; // y columna2 será d2 + c2
// Ahora tenemos que comprobar si las nuevas col1 y col2 están en el rango de 0 y col. Y para eso necesitamos crear un nuevo método, que verificará si las nuevas col1 y col2 están en el rango
tejo(en el rango(col1, collar) && en el rango(col2, collar)){
doble penetración[I][col1][col2] = Matemáticas.max(doble penetración[I][col1][col2], anterior+(col1 == col2 ? red[I][col1] : (red[I][col1] + red[I][col2]))); // si el valor está dentro de este rango, necesitamos actualizar la posición col1 y col2 en la i-ésima fila
max = Matemáticas.max(max, doble penetración[I][col1][col2]); // necesitamos actualizar el máximo en cada paso. Tomando el valor máximo del valor máximo y también la nueva columna que hemos llenado
}
}
}
}
}
}
}
regreso max; //regreso máximo al finalLlamemos a dp' el enfoque ascendente. Aquí hay un código mejor optimizado usando un enfoque de arriba hacia abajo para el problema original.
dp[k][i][j] indica si los dos robots parten de grid[k][i] y grid[k][j], el número total máximo de cerezas que finalmente pueden recoger. Tenga en cuenta que solo pueden moverse hacia abajo.
Después de llenar dp, la respuesta final es dp[0][0][COL_NUM – 1]
Para la última línea de la cuadrícula, tenemos dp[-1][i][j] = grid[-1][i] if i == j else grid[-1][i] + grid[-1][ j ]. Tenga en cuenta que si 2 robots permanecen en el mismo lugar, solo pueden recoger una vez.
Para las otras filas, tenemos que iterar sobre todas las combinaciones de 3*3 direcciones que pueden elegir en la siguiente capa y encontrar el máximo, porque para cada robot hay 3 direcciones en las que pueden moverse.
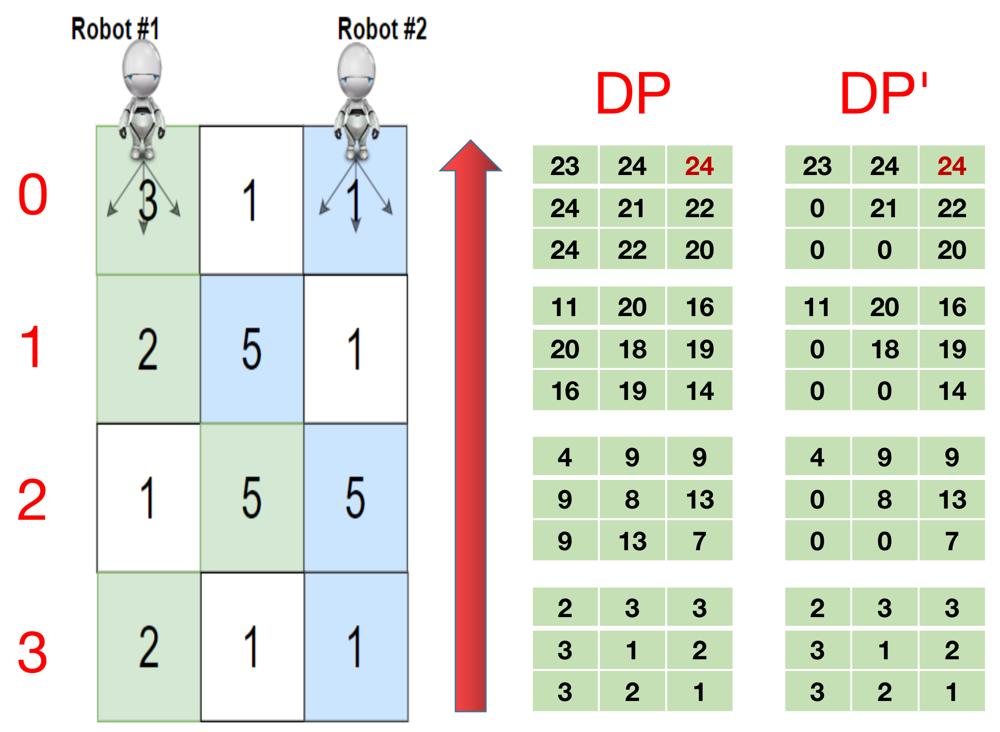
Tendremos por tanto el siguiente código:

No es muy óptimo. Aquí hay un código mejor optimizado en python (en 2D con un enfoque DFS):