Contenido
PalancaCorrelación y Regresiones
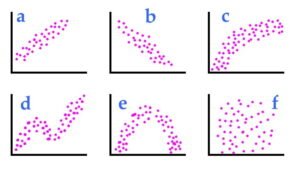
En estadística, correlación o dependencia es cualquier relación estadística, causal o no, entre dos variables aleatorias o datos bivariados. Aunque en el sentido más amplio "correlación" puede indicar cualquier tipo de asociación, en estadística normalmente se refiere al grado en que un par de variables se relaciona linealmente. Ejemplos familiares de fenómenos dependientes incluyen la correlación entre el tamaño de los padres y su descendencia, y la correlación entre el precio de un bien y la cantidad que los consumidores están dispuestos a comprar, como se representa en la llamada curva de demanda.
Las correlaciones son útiles porque pueden indicar una relación predictiva que se puede usar en la práctica. Por ejemplo, una empresa de servicios públicos de electricidad puede producir menos electricidad en un clima templado dependiendo de la correlación entre la demanda de electricidad y las condiciones climáticas. En este ejemplo, existe una relación causal, ya que el clima extremo hace que las personas usen más electricidad para calentar o enfriar. Sin embargo, en general, la presencia de una correlación no es suficiente para inferir la presencia de una relación causal (es decir, la correlación no implica causalidad).
En el modelado estadístico, el análisis de regresión es un conjunto de procesos estadísticos para estimar las relaciones entre una variable dependiente (a menudo llamada variable de "resultado" o "respuesta") y una o más variables independientes (a menudo llamadas "predictores"), 'covariables' , 'variables explicativas' o 'características'). La forma más común de análisis de regresión es la regresión lineal, en la que se encuentra la línea (o una combinación lineal más compleja) que mejor se ajusta a los datos según un criterio matemático específico.
Por ejemplo, el método de mínimos cuadrados ordinarios calcula la línea única (o hiperplano) que minimiza la suma de las diferencias al cuadrado entre los datos verdaderos y esa línea (o hiperplano). Por razones de Matemáticas (ver regresión lineal), esto le permite al investigador estimar la expectativa condicional (o valor medio de la población) de la variable dependiente cuando las variables independientes toman un conjunto dado de valores. Las formas menos comunes de regresión utilizan procedimientos ligeramente diferentes para estimar parámetros de ubicación alternativos (p. ej., regresión por cuantiles o análisis de condiciones necesarias) o estiman la expectativa condicional en una colección más grande de modelos no lineales (por ejemplo, regresión no paramétrica).
El análisis de regresión se utiliza principalmente para dos propósitos conceptualmente distintos.
Primero, el análisis de regresión se usa ampliamente para la predicción y el pronóstico, donde su uso se superpone significativamente con el campo del aprendizaje automático.
En segundo lugar, en algunas situaciones, el análisis de regresión se puede utilizar para inferir relaciones causales entre variables independientes y dependientes. Es importante señalar que las regresiones por sí solas solo revelan las relaciones entre una variable dependiente y un conjunto de variables independientes en un conjunto de datos fijo. Para usar regresiones para la predicción o para inferir relaciones causales, respectivamente, un investigador debe justificar cuidadosamente por qué las relaciones existentes tienen poder predictivo para un nuevo contexto o por qué una relación entre dos variables tiene una interpretación causal. Esto último es particularmente importante cuando los investigadores esperan estimar las relaciones causales utilizando datos de observación.