Contenus
ToggleCorrélation et Régressions
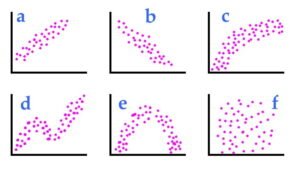
En statistique, la corrélation ou la dépendance est toute relation statistique, causale ou non, entre deux variables aléatoires ou données bivariées. Bien qu’au sens le plus large, la « corrélation » puisse indiquer n’importe quel type d’association, en statistique, elle fait normalement référence au degré auquel une paire de variables est linéairement liée. Des exemples familiers de phénomènes dépendants incluent la corrélation entre la taille des parents et leur progéniture, et la corrélation entre le prix d’un bien et la quantité que les consommateurs sont prêts à acheter, telle qu’elle est représentée dans la courbe dite de demande.
Les corrélations sont utiles car elles peuvent indiquer une relation prédictive exploitable en pratique. Par exemple, un service public d’électricité peut produire moins d’électricité par temps doux en fonction de la corrélation entre la demande d’électricité et les conditions météorologiques. Dans cet exemple, il existe une relation causale, car les conditions météorologiques extrêmes poussent les gens à utiliser plus d’électricité pour le chauffage ou la climatisation. Cependant, en général, la présence d’une corrélation n’est pas suffisante pour déduire la présence d’une relation causale (c’est-à-dire que la corrélation n’implique pas la causalité).
Dans la modélisation statistique, l’analyse de régression est un ensemble de processus statistiques permettant d’estimer les relations entre une variable dépendante (souvent appelée variable « résultat » ou « réponse ») et une ou plusieurs variables indépendantes (souvent appelées « prédicteurs », « covariables », ‘variables explicatives’ ou ‘caractéristiques’). La forme la plus courante d’analyse de régression est la régression linéaire, dans laquelle on trouve la ligne (ou une combinaison linéaire plus complexe) qui correspond le mieux aux données selon un critère mathématique spécifique.
Par exemple, la méthode des moindres carrés ordinaires calcule la ligne unique (ou hyperplan) qui minimise la somme des différences au carré entre les vraies données et cette ligne (ou hyperplan). Pour des raisons mathématiques spécifiques (voir régression linéaire), cela permet au chercheur d’estimer l’espérance conditionnelle (ou valeur moyenne de la population) de la variable dépendante lorsque les variables indépendantes prennent un ensemble de valeurs donné. Les formes de régression moins courantes utilisent des procédures légèrement différentes pour estimer les paramètres de localisation alternatifs (par exemple, la régression quantile ou l’analyse des conditions nécessaires) ou estimer l’espérance conditionnelle à travers une collection plus large de modèles non linéaires (par exemple, la régression non paramétrique).
L’analyse de régression est principalement utilisée à deux fins conceptuellement distinctes.
Premièrement, l’analyse de régression est largement utilisée pour la prédiction et la prévision, où son utilisation chevauche considérablement le domaine de l’apprentissage automatique.
Deuxièmement, dans certaines situations, l’analyse de régression peut être utilisée pour déduire des relations causales entre les variables indépendantes et dépendantes. Il est important de noter que les régressions en elles-mêmes ne révèlent que les relations entre une variable dépendante et un ensemble de variables indépendantes dans un ensemble de données fixe. Pour utiliser des régressions pour la prédiction ou pour déduire des relations causales, respectivement, un chercheur doit justifier soigneusement pourquoi les relations existantes ont un pouvoir prédictif pour un nouveau contexte ou pourquoi une relation entre deux variables a une interprétation causale. Ce dernier est particulièrement important lorsque les chercheurs espèrent estimer les relations causales à l’aide de données d’observation.