Algorithmique 101 - Complex systems and AI

I. Écriture et modélisation d'un algorithme

Analysis:

II. Paradigmes et stratégies de programmation

Contenu de va-et-vient

Contenus

Algorithmique

L’algorithmique existe depuis toujours, il s’agit d’un processus de pensée décrit de manière logique. Bien que ce système nous semble aujourd’hui indispensable pour nombres de sciences, la systématisation de l’écriture algorithmique a évolué au cours du temps et des technologies. Elle a commencé du temps des babyloniens, jusqu’à être concrètement établi par René Descartes dans la méthode générale proposée par le Discours de la méthode en 1637.

L’algorithmique moderne, comprenant un langage dit de « programme » fait ses débuts peu de temps après en 1677. Le terme que l’on utilise de nos jours, « algorithme », apparaît quant à lui deux siècles plus tard.

L’algorithmique du XX^e et du XXI^e siècle se base souvent sur des formalismes comme celui des machines de Turing, qui donne un cadre scientifique pour étudier les propriétés des algorithmes.

Avec l’informatique, l’algorithmique s’est beaucoup développée dans la deuxième moitié du XX^e siècle et Knuth (1969), auteur de The Art of Computer Programming définit 5 propriétés qui constituent les pré-requis d’un algorithme.

1. Finitude : un algorithme doit se terminer après un nombre fini d’étapes

2. Définition précise : chaque étape d’un algorithme doit être définie précisément sans ambigüité

3. Entrées : des quantités qui sont définie avant que l’algorithme ne commence

4. Sorties : des quantités qui ont une relation spécifiée avec les entrées

5. Rendement : toutes les opérations que l’algorithme doit accomplir, doivent être suffisamment basiques pour pouvoir en principe être réalisées dans une durée finie par un homme utilisant du papier et un crayon.

Markov (1967) définit un algorithme comme « Une prescription exacte définissant un processus de traitement qui mène à partir de données initial au résultat final ».

Ce qui implique les caractéristiques suivantes :
• Précision de la prescription ne laissant aucune place à l’arbitraire et compréhension universelle • Possibilité de démarrer avec des données initiales pouvant varier dans des limites données • L’orientation de l’algorithme dans la recherche d’un résultat voulu qui doit s’obtenir à la fin de l’exécution à partir des données initiales : c’est la propriété de conclusion de l’algorithme.

Pour Minsky (1967) la définition est encore plus directe:
« Un ensemble de règles qui nous dit, d’instant en instant, comment précisément se comporter »

Et enfin pour Stone (1972)
« Un algorithme est un ensemble de règles qui définit précisément une séquence d’opérations de sorte que chaque règle soit effective et définie et que la séquence se termine dans un temps fini. »

Il précise en complément que :
« pour ceux qui suivent les règle de l’algorithme, elles doivent être formulées de sorte qu’elles soient suivies mécaniquement sans avoir à penser »

Par exemple :
Si les instructions nécessitent l’extraction d’une racine carrée et sont effectuées par quelqu’un qui sait faire les opérations arithmétiques mais qui ne sait pas extraire une racine carrée, alors on doit fournir un ensemble de règles pour extraire une racine carrée, afin de satisfaire à définition de l’algorithme

De nombreux outils formels ou théoriques ont été développés pour décrire les algorithmes, les étudier, exprimer leurs qualités, pouvoir les comparer :

des structures algorithmiques : structures de contrôle et structures de données.
les notions de correction, de complétude et de terminaison.
la théorie de la complexité.

Transcrire un algorithme

Le langage naturel : verbeux et ambigü, rarement utilisé pou des algorithmes complexes mais pas interdit.
Pseudo-code : un langage structuré, mais pas de règles strictes définies; Indépendant de toute implémentation
Organigramme : pas d’ambigüité, bonne lisibilité, écriture sous forme de symboles normalisés
Langages de programmation : normalement destinés à transcrire les organigrammes sous une forme compréhensible par les ordinateurs ; peuvent être aussi utilisés pour décrire les algorithmes
Langages d’algorithmique : langage utilisant un pseudo-code composé de règles fixes, compréhensible par un ordinateur, permettant la description et l’exécution des algorithmes.

Structure de contrôle et structure de données

Une structure de contrôle est une commande qui contrôle l’ordre dans lequel les différentes instructions d’un algorithme ou d’un programme informatique sont exécutées. Le processeur est chargé de mémoriser l’adresse de la prochaine instruction à exécuter, les blocs (boucles, if, etc) ou les sous-programmes.

On appelle aussi cet enchaînement d’instructions le flot d’exécution d’un programme et on peut le représenter à l’aide d’un graphe de flot de contrôle ou un automate. Certain paradigme de programmation faisant appel à plusieurs processeur s’expose alors au problème d’affectation des tâches dans les processeurs.

Une structure de données est une structure logique destinée à contenir des données, afin de leur donner une organisation permettant de simplifier leur traitement. Il existe de nombreux types de structure de données en fonction des actions à effectuer sur ces dernières, nous ne tarderons pas plus sur ce sujet.

Chaque langage informatique possède un type de structure de contrôle et structure de données. L’écriture d’un algorithme se base très souvent sur des langages très répandus tels que le C, le java, etc.

Notions de terminaison, de correction, de complétude

La terminaison est l’assurance que l’algorithme terminera en un temps fini. Les preuves de terminaison font habituellement intervenir une fonction entière positive strictement décroissante à chaque étape/itération de l’algorithme.

Étant donnée la garantie qu’un algorithme terminera, la preuve de correction doit apporter l’assurance que si l’algorithme termine en donnant une proposition de solution, alors cette solution est correcte (dans le sens où elle répond au problème posé).

La preuve de complétude garantit que, pour un espace de problèmes donné, l’algorithme, s’il termine, donnera une solution pour chacune des entrées de l’algorithme.

Terminaison : l’algorithme possède une complexité en temps.

Correction : toute réponse calculée de l’algorithme est solution du problème.

Complétude : l’algorithme peut calculer une réponse pour toute instance du problème.

Complexité algorithmique

La complexité des algorithmes est une évaluation du coût d’exécution d’un algorithme en termes de temps (complexité temporelle) ou d’espace mémoire (complexité spatiale). L’efficacité d’un algorithme dépend donc de ces deux critères, que l’on cherchera à minimiser.

La complexité algorithmique permet de s’informer sur l’efficacité intrinsèque d’un
algorithme : la performance « naturelle » d’un algorithme en dehors de l’environnement dans lequel sera implémenté ce dernier.

Il existe plusieurs types d’analyse de la performance d’un algorithme :

L’analyse optimiste (analyse dans le cas le plus favorable ou analyse dans le meilleur des cas).
L’analyse en moyenne est souvent facteur du paradigme de programmation utilisé.
L’analyse pessimiste (analyse dans le cas le plus défavorable ou analyse dans le pire des cas).

Les classes de complexité sont des ensembles de problèmes qui ont la propriété d’avoir tous la même complexité selon un certain critère. Les classes les plus connues sont des classes définies sur des machines de Turing (déterministes ou non déterministes – voir le cours sur les automates) avec des contraintes de temps et d’espace. Il existe une relation entre la complexité algorithmique et son coût énergétique de fonctionnement, appelé principe de Landauer.

Voici une liste des complexités les plus fréquemment rencontrées :

Notation	Type de complexité
$O(1)$	complexité constante : une affectation, un calcul élémentaire, etc.
$O(\log(n))$	complexité logarithmique : dichotomie, arbre
$O(n)$	complexité linéaire : une boucle
$O(n \log(n))$	complexité quasi-linéaire : diviser pour régner, arbre
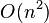$O(n^{2})$	complexité quadratique : imbrication deux boucles
$O(n^{3})$	complexité cubique : imbrication de trois boucles
$O(n^p)$	complexité polynomiale : imbrication de boucles sans connaissance d’états
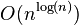$O(n^{\log(n)})$	complexité quasi-polynomiale : diviser pour régner
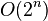$O(2^{n})$	complexité exponentielle : arbre, force brute
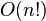$O(n!)$	complexité factorielle : approche naïve d’énumération combinatoire