Voici un pipeline expliquant l’exploration des données, leur transformation pour normalisation et la régression (avec analyse de performance).

Contenus
ToggleAnalyse, transformation et régression
Plongeons maintenant dans l’autre catégorie d’apprentissage supervisé – la régression où la variable de sortie est continue et numérique. Il existe quatre types courants de modèles de régression : linéaire, au lasso, de crête (ridge regression), polynomiale.
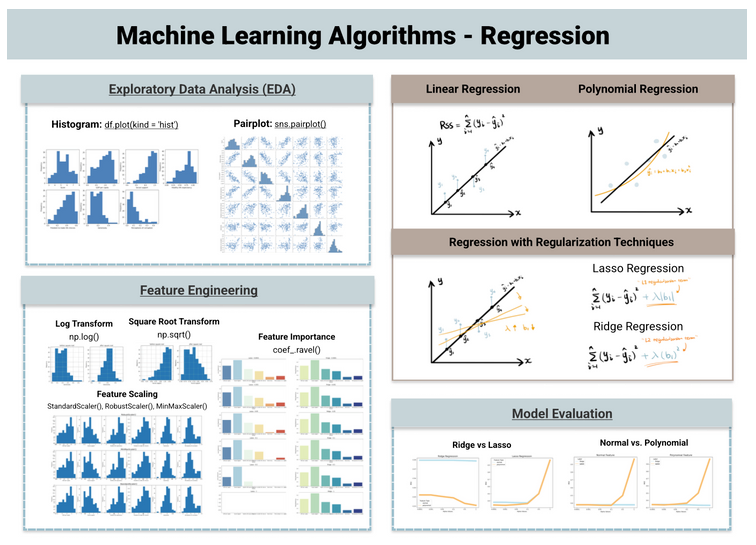
Exploration et préprocessing
Ce projet vise à utiliser des modèles de régression pour prédire les scores de bonheur des pays en fonction d’autres facteurs « PIB par habitant », « Soutien social », Espérance de vie en bonne santé », « Liberté de faire des choix de vie », « Générosité » et « Perceptions de la corruption ».
J’ai utilisé l’ensemble de données « World Happiness Report » sur Kaggle, qui comprend 156 entrées et 9 fonctionnalités.
Appliquez l’histogramme pour comprendre la distribution de chaque fonctionnalité. Comme indiqué ci-dessous, le «soutien social» semble être fortement biaisé à gauche tandis que la «générosité» et les «perceptions de la corruption» sont biaisées à droite – ce qui informe les techniques d’ingénierie des fonctionnalités pour la transformation.
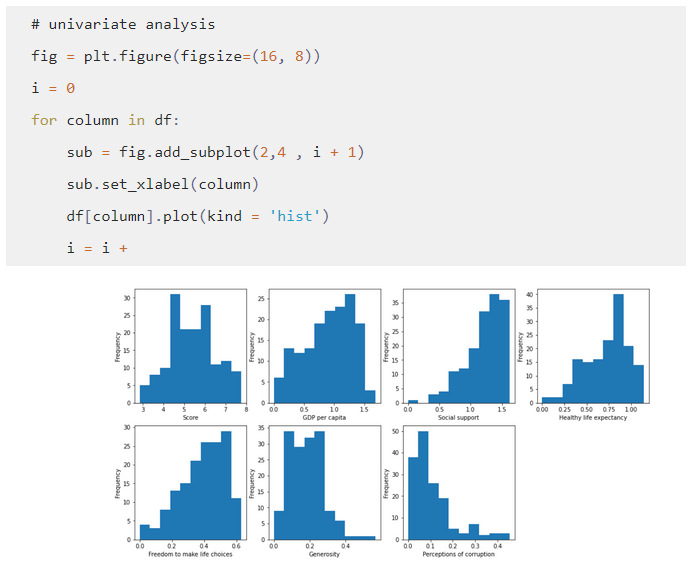
Nous pouvons également combiner l’histogramme avec la mesure d’asymétrie ci-dessous pour quantifier si la caractéristique est fortement asymétrique à gauche ou à droite.

np.sqrt est appliqué pour transformer les caractéristiques asymétriques à droite – « Générosité » et « Perceptions de la corruption ». En conséquence, les deux caractéristiques deviennent plus normalement distribuées.
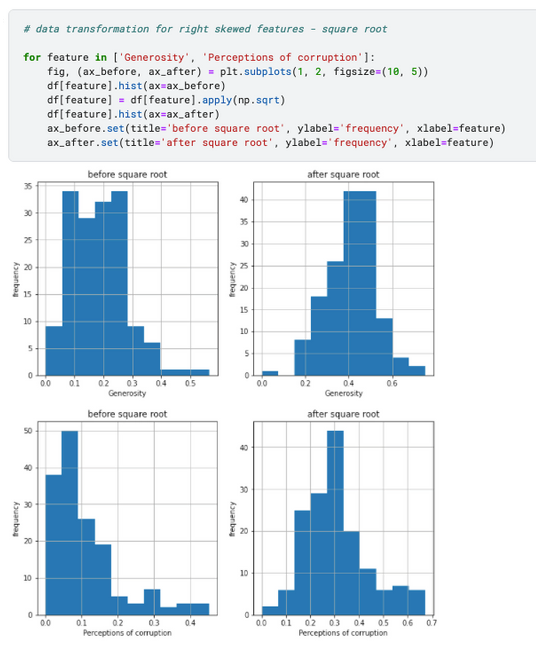
np.log(2-df[‘Social support’]) est appliqué pour transformer la fonction asymétrique à gauche. Et l’asymétrie diminue considérablement de 1,13 à 0,39.
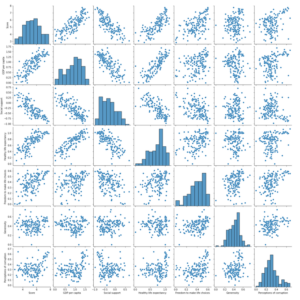
sns.pairplot(df) peut être utilisé pour visualiser la corrélation entre les entités après la transformation. Les diagrammes de dispersion suggèrent que « PIB par habitant », « Soutien social », « Espérance de vie en bonne santé » sont corrélés avec la caractéristique cible « Score », et peuvent donc avoir des valeurs de coefficient plus élevées. Découvrons si c’est le cas dans la section ultérieure.
Étant donné que les techniques de régularisation manipulent la valeur des coefficients, cela rend les performances du modèle sensibles à l’échelle des caractéristiques. Par conséquent, les entités doivent être transformées à la même échelle. J’ai expérimenté sur trois échelles – StandardScaler, MinMaxScaler et RobustScaler.
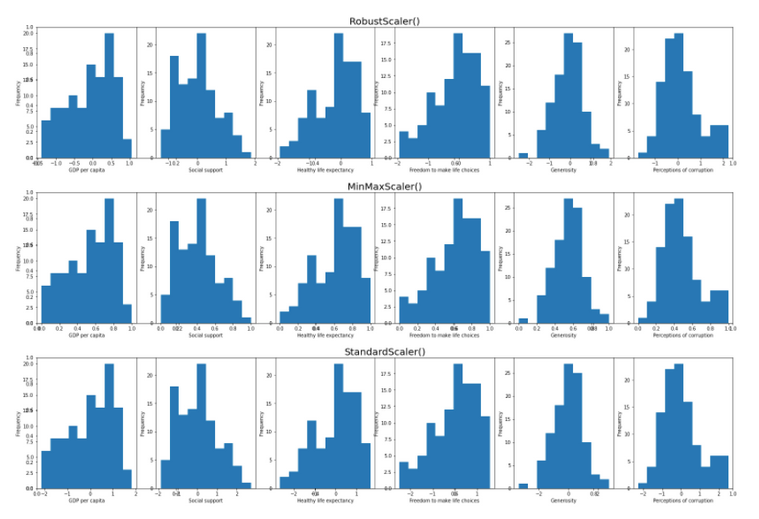
Comme vous pouvez le voir, les échelles n’affecteront pas la distribution et la forme des données, mais modifieront la plage des données.
Régressions et comparaisons
Comparons maintenant trois modèles de régression linéaire ci-dessous – linéaire, de crête et de lasso.

L’étape suivante consiste à expérimenter comment différentes valeurs lambda (alpha dans scikit-learn) affectent les modèles. Plus important encore, comment l’importance des caractéristiques et les valeurs de coefficient changent lorsque la valeur alpha passe de 0,0001 à 1.
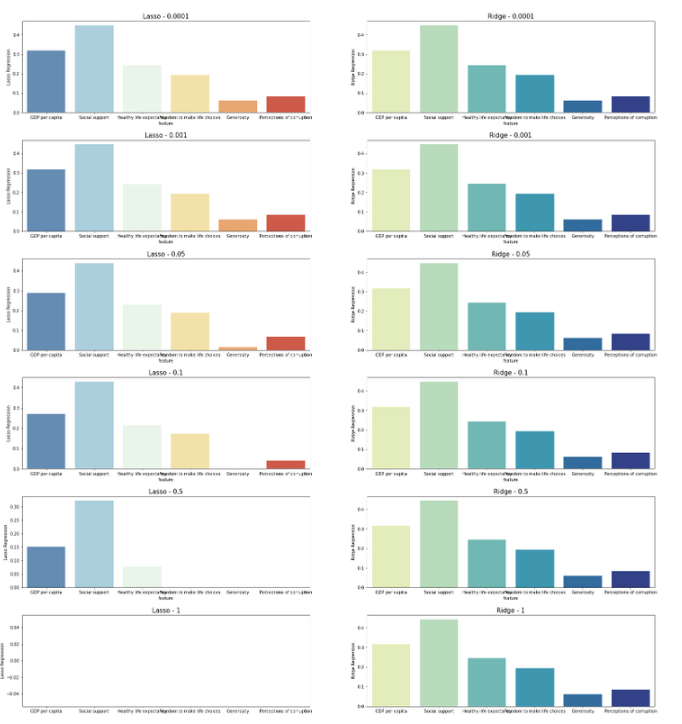
Sur la base des valeurs de coefficients générées à partir des modèles Lasso et Ridge, « PIB par habitant », « Soutien social », « Espérance de vie en bonne santé » semblaient être les 3 caractéristiques les plus importantes. Ceci est aligné sur les résultats des diagrammes de dispersion précédents, suggérant qu’ils sont les principaux moteurs du Country Happy Score.
La comparaison côte à côte indique également que l’augmentation des valeurs alpha a un impact sur Lasso et Ridge à différents niveaux, les fonctionnalités de Lasso sont plus fortement supprimées. C’est pourquoi Lasso est souvent choisi pour la sélection des fonctionnalités.
De plus, des caractéristiques polynomiales sont introduites pour améliorer la régression linéaire de base, ce qui augmente le nombre de caractéristiques de 6 à 27.
# apply polynomial effects
from sklearn.preprocessing import PolynomialFeatures
pf = PolynomialFeatures(degree = 2, include_bias = False)
X_train_poly = pf.fit_transform(X_train)
X_test_poly = pf.fit_transform(X_test)Regardez leur distribution après la transformation polynomiale.
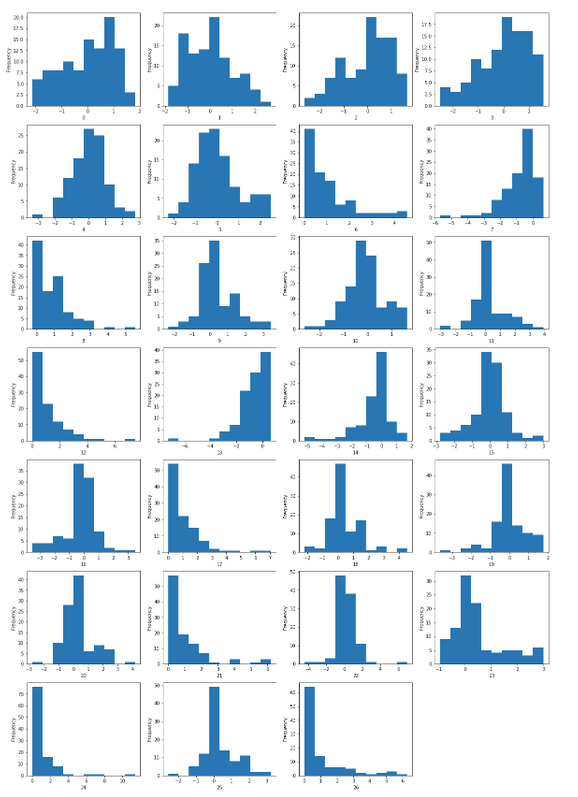
Evaluation des modèles
Dernière étape, évaluez et comparez les performances du modèle Lasso vs de crête, avant et après effet polynomial. Dans le code ci-dessous, j’ai créé quatre modèles :
- l2 : de crête sans caractéristiques polynomiales
- l2_poly : de crête avec caractéristiques polynomiales
- l1 : de lasso sans caractéristiques polynomiales
- l1_poly : de lasso avec caractéristiques polynomiales

Les métriques d’évaluation de modèle de régression couramment utilisées sont MAE, MSE, RMSE et R au carré – consultez mon article sur « Un guide pratique de la régression linéaire » pour une explication détaillée. Ici, j’ai utilisé MSE (erreur quadratique moyenne) pour évaluer les performances du modèle.
1) En comparant Ridge et Lasso dans un graphique, cela indique qu’ils ont une précision similaire lorsque les valeurs alpha sont faibles, mais que le Lasso se détériore considérablement lorsque l’alpha est plus proche de 1.
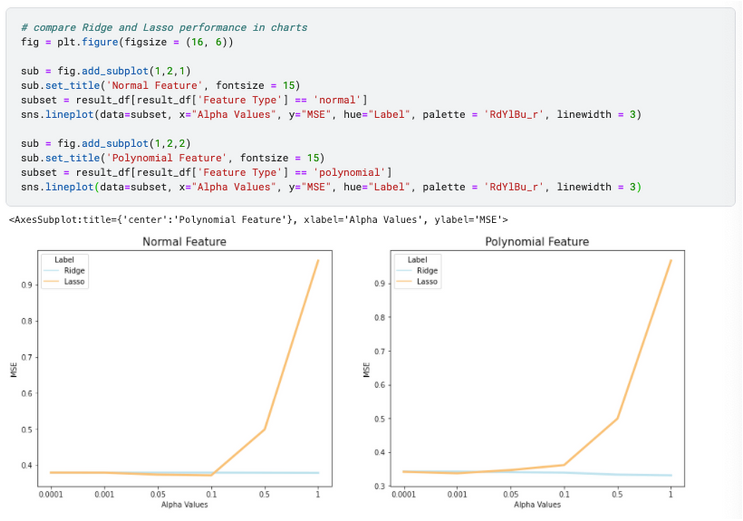
2) En comparant avec ou sans effet polynomial dans un graphique, nous pouvons dire que le polynôme diminue la MSE en général – donc améliore les performances du modèle. Cet effet est plus significatif dans la régression Ridge lorsque alpha augmente à 1, et plus significatif dans la régression Lasso lorsque alpha est plus proche de 0,0001.
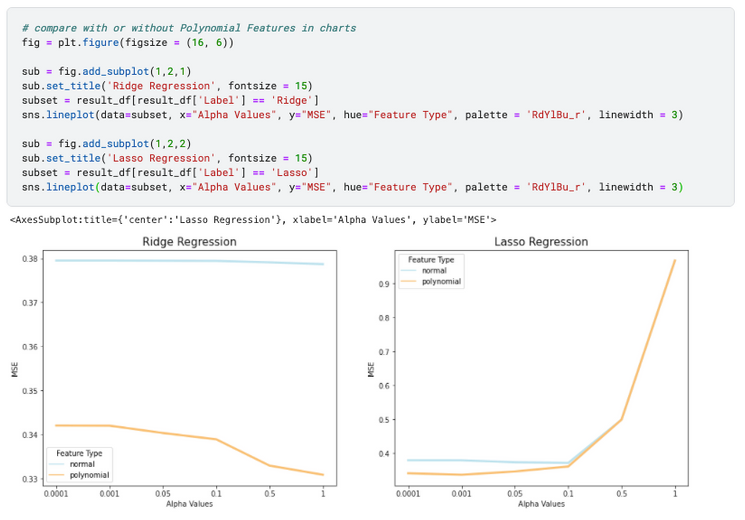
Cependant, même si la transformation polynomiale améliore les performances des modèles de régression, elle rend l’interprétabilité du modèle plus difficile – il est difficile de distinguer les principaux moteurs du modèle d’une régression polynomiale. Moins d’erreur ne garantit pas toujours un meilleur modèle, et il s’agit de trouver le bon équilibre entre prévisibilité et interprétabilité en fonction des objectifs du projet.
