Encontrar caminos 101

Búsqueda de ruta

los búsqueda de ruta, comunmente llamado camino consiste en encontrar cómo moverse en un entorno entre un punto de partida y un punto final teniendo en cuenta varias limitaciones.

Definición de un gráfico valorado

Una gráfica valorada es una gráfica a cuyos arcos asociamos un número real llamado longitud del arco.

Denotamos por w (x, y) la longitud del arco (x, y) entre los vértices xey.

Por analogía con la matriz de adyacencia, podemos representar un gráfico valorado por una matriz cuadrada, cuyos coeficientes corresponden a la valoración de los arcos.

Sea un gráfico valorado cuyos vértices se han numerado de 1 a n. La matriz de valoración de G es la matriz cuadrada M = m_ij, de tamaño n * n, definido por

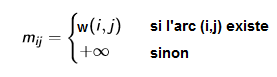
Aquí hay un ejemplo:

Por tanto, podemos deducir el siguiente programa lineal, con x_ij= 1 si el arco es parte de la ruta más corta, 0 en caso contrario:

• minimizar con A el conjunto de arcos
• sujeto a

y para todos I,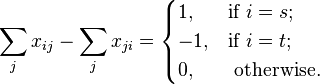

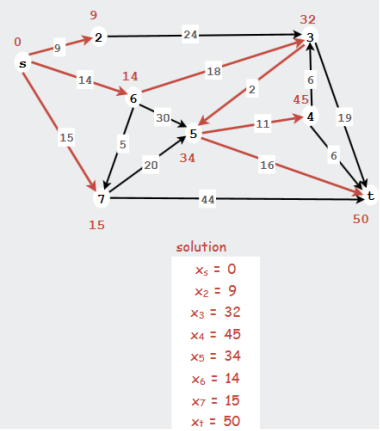
Aunque se trata de programación lineal, este método puede resultar muy caro en memoria, e incluso imposible de configurar en determinados casos (por ejemplo, si se trata de un sistema distribuido). Otro método para conocer el camino más corto sería conocer el más pequeño de todos los caminos de un vértice a otro.

Definimos el peso de un camino c = (u,…, v)

como la suma de los pesos de los arcos que lo constituyen anotado WC).Luego definimos la distancia mínima (camino más corto) entre dos vértices u y v por:

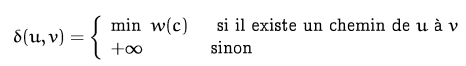
Nos gustaría tener un método capaz, para cualquier gráfico y para cualquier par de vértices. X y y, para determinar el camino más corto entre ellos. Para ello, debemos comprender y caracterizar lo mejor posible la estructura de una solución: ¿cuáles son las propiedades de un camino más corto?

Lema de Koenig. Un camino más corto entre 2 vértices es elemental. Un sendero es elemental si cada uno de los picos de la ruta se visita una sola vez.

Enumerar todos los caminos para determinar el más corto revela un grave defecto: su tiempo de ejecución. Si el número de caminos elementales es finito, no obstante sigue siendo muy grande, del orden de ¡no! en un gráfico de orden no.

Problema subóptimo

Necesitamos una segunda propiedad fundamental, la suboptimalidad (ver Programación dinámica). Es cuestión de notar que ser un camino más corto es recursivo: una secuencia de un camino más corto sigue siendo un camino más corto entre sus extremos. O si la ruta más rápida entre tu y v pasa por 2 picos X y y, esta ruta necesariamente toma el camino más corto entre X y y.

sí p = (u,…, v) es un camino más corto entre tu y v, luego para cualquier cumbre X en el camino pag :

• el subtrayecto de pag hasta X, (u,…, x), es un camino más corto de tu Para X
• el subtrayecto de pag desde X, (x,…, v), es un camino más corto de X Para v

Para el absurdo supongamos que existe, por ejemplo, entre tu y X un camino q de longitud estrictamente menor que la de p = (u,…, x,…, v). Para que podamos construir un nuevo camino pag ' Entre tu y v sustituyendo q seguro (u,…, x) en la forma pag. El largo de pag ' es entonces estrictamente menor que el de pag, que contradice que pag es una forma más corta de tu Para v.

Árbol de caminos

Hay un árbol Hay un árbol que muestra los caminos más cortos desde un punto de partida a todos los demás. Suponga que la gráfica está conectada, los bordes no están dirigidos y los pesos no son negativos. Desarrollamos una nube de vértices, comenzando con sy finalmente cubriendo todos los vértices. Almacenamos en cada vértice v una etiqueta d (v) que representa la distancia de v desde s en el subgrafo formado por la nube y sus vértices adyacentes. En cada paso: agregamos a la nube la parte superior fuera de la nube con la etiqueta de distancia más pequeña; actualizamos las etiquetas de los vértices adyacentes a u (ver árbol de expansión).

Considere una arista e = (u, z) tal que u es el vértice agregado más recientemente a la nube yz no está en la nube. La relajación del borde e actualiza la distancia d (z) de la siguiente manera: d (z) ← min {d (z), d (u) + peso (e)}