Contenido
PalancaFlujo maximo
El flujo máximo para modelar una clase muy grande de problemas. Su interpretación corresponde a la circulación de flujos físicos en una red: distribución eléctrica, red de aducción, enrutamiento de paquetes en Internet, etc. Esto implica transportar la mayor cantidad posible de material entre una fuente s y un destino t.
Definición de una red
Una red es un grafico orientada N=(V,A) con una valoración positiva de sus arcos. La valoración c(x,y) de un arco (x,y) se llama capacidad del arco. N tiene dos vértices particulares: un origen s y un destino t. Los otros vértices se denominan nodos intermedios.
Un flujo representa el enrutamiento de un flujo de materiales desde una fuente. s a un destino t. El flujo se describe así por la cantidad de material que pasa por cada uno de los arcos de la red. Esta cantidad debe ser menor que la capacidad del arco, lo que limita el flujo que puede atravesarlo. Además, no es posible almacenar o producir materia en los nodos intermedios: un flujo verifica localmente una ley de conservación similar a las leyes de Kirchhoff en electricidad.
Un flujo F en una red N es una valoración positiva de los arcos que satisface las siguientes dos propiedades:
- Para cualquier arco un ∈ PARA, 0 ≤ F (a)≤ese)
- Para cualquier cumbre intermedia X∈V \ { S t }, ∑y F (y, x) = ∑y F (x, y)
La suma F–(X) =∑yF (y, x) es el afluencia en la cima X
La suma F+(X) =∑yF (x, y) es el flujo saliente Cumbre X
los valor | F | de una inundación F se define como el flujo saliente menos el flujo entrante en s : | F | = F+(s) – F–(s).
Problema de flujo máximo
El problema clásico de flujo máximo es un problema lineal. Suponemos que la red tiene aristas entre cualquier par de vértices. Si no hay capacidad, se fija en 0. La función objetivo es la suma de los flujos que salen de la fuente o entran en el sumidero. La función de la lente puede variar dependiendo de la lente.
Las restricciones básicas son idénticas cualquiera que sea la función objetivo:
- Restricciones de capacidad: f (u, v) ≤ c (u, v)
- Simetría: f (u, v) = - f (v, u)
- Conservación de caudales: la suma de los caudales entrantes es igual a la suma de los caudales salientes a excepción de la fuente y el sumidero, el grado d (u) se llama la diferencia entre el caudal saliente y entrante del vértice u: d ( u) = 0 excepto para u = sy u = t.
- otros
Muchos problemas se remontan a un problema de flujo máximo. A algoritmo ingenuo es repetir el siguiente proceso hasta que te quedes atascado. Encuentre un camino st donde cada arco af(e)
Reducción de problemas
Problema de flujo de múltiples fuentes y múltiples pozos : una fuente ficticia está conectada a todas las fuentes, la capacidad de los bordes depende de varios criterios (capacidad de los vértices, restricciones de entrada-salida). Los pozos están conectados a un pozo ficticio. Este tipo de problema suele ser un problema de emparejamiento.
Problema de flujo con capacidad en los picos : los vértices se duplican en el vértice de entrada y el vértice de salida con un arco que los conecta. La capacidad de este arco es igual a la capacidad de la tapa.
Problema de camino más corto : la fuente es el origen de la ruta y el sumidero con d (s) = 1 y d (t) = - 1. No hay limitaciones de capacidad. El costo de paso en todos los arcos es 1. Buscamos el flujo de costo mínimo.
Corte de red y capacidad residual
Un corte (E, T) de una red de transporte N = (V, A) es una partición de V en E y T = VE tal que s ∈E y t∈T. Definimos la capacitancia c (E, T) de la sección transversal la suma de las capacitancias de los arcos (u, v) con u en E yv en T. Para cualquier sección transversal (E, T) y cualquier flujo f, | f | se incrementa por la capacidad del corte c (E, T).
Quite un juego de bordes para desconectar t de s. Encuentre un conjunto para minimizar la suma de las capacidades de los arcos. Un corte mínimo es una partición de nodos (S, T) tal que s está en S yt en T donde c (E, T) es mínimo. Por definición, el problema de corte mínimo tiene el mismo resultado que un problema de flujo máximo.
Dada una red N = (V, A) y un flujo f sobre N, llamamos capacidad residual cF (u, v) = c (u, v) - f (u, v). Además, si la capacidad de (v, u) es cero, cF (v, u) = f (u, v). La capacidad residual es siempre positiva o nula.
El gráfico residual es la red N '= (V, A) con las capacidades residuales para cada arco de A. Una trayectoria creciente es una trayectoria entre syt en el gráfico residual.

A partir del gráfico residual de un flujo máximo, es posible encontrar la solución del problema de corte mínimo (y viceversa). En la siguiente gráfica, si encuentra un conjunto de vértices conectados desde el vértice s, encuentra el conjunto {s, 3, 4, 7} que es el conjunto S para el problema de corte mínimo.
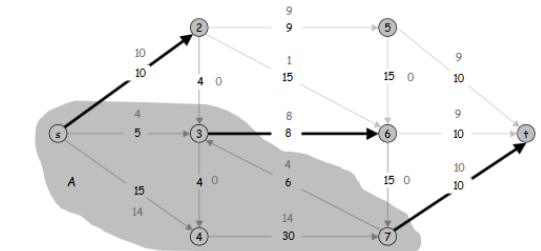
Encuentra un flujo creciente
Encuentre un camino st en el gráfico residual, se llama camino creciente. Una vez que se selecciona la ruta, aumente el flujo a lo largo de los arcos en la misma dirección que el gráfico estándar, disminuya el flujo a lo largo de los arcos hacia atrás.

