Teoría de grafos 101: sistemas complejos e inteligencia artificial

Contenido

Teoría de grafos

En teoría de grafos, un gráfico GRAMO se define por una pareja (S, A) con S un conjunto finito de vértices, y PARA un conjunto finito de pares de vértices (s_I, s_j) en S².

En un gráfico dirigido, los pares (s_I, s_j) de PARA están orientados, es decir, s_I es el vértice inicial ys_j el vértice terminal. Gráficamente, esta pareja es una inclinarse desde la parte superior s_I hacia la cima s_j.

En un gráfico no dirigido, los pares (s_I, s_j) no están orientados. Por lo tanto, (s_I, s_j) es equivalente a escribir (s_j, s_I). Gráficamente, esta pareja es una espina de pescado entre vértices s_I ys_j.

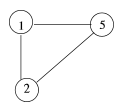
Elementos de terminología:

LOS'pedido de una gráfica es el número de sus vértices | S |.
A círculo es un arco o un borde (s_I, s_I).
Se dice un gráfico no dirigido sencillo si no contiene un bucle y si tiene como máximo un borde entre cualquier par de vértices. De lo contrario, es un gráfico múltiple.
Se dice un grafo dirigido elemental si no contiene un bucle.
Un gráfico dirigido es un gráfico p si tiene como máximo pag arcos entre cualquier par de vértices.
Un gráfico partiel de un gráfico es el gráfico que se obtiene al eliminar ciertos arcos (o aristas).
a subgrafo de un gráfico es el gráfico que se obtiene al eliminar ciertos vértices y todos los arcos incidentes a los vértices eliminados.
Se dice una gráfica lleno si tiene un borde (s_I, s_j) para cualquier par de vértices (o dos arcos (s_I, s_j) y (s_j, s_I)). Un gráfico simple completo con n vértices tendrá n (n-1) / 2 aristas.
a atributo se puede asociar con (s_I, s_j). El atributo puede ser una letra, una palabra o un peso (valor numérico). Una gráfica con pesos se llama La red.

Considere una gráfica G = (V, E, w) con una función de peso:

Nociones de adyacencia:

En un gráfico no dirigido, un vértice s_I es dicho adyacente en una cumbre s_j si hay una ventaja entre s_I ys_j. El conjunto de vértices adyacentes a un vértice s_I es definido por:

En un grafo dirigido, distinguimos los vértices sucesores (terminales de un arco) y antecesores (iniciales de un arco):

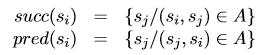
Nociones de grado de un vértice:

En un gráfico no dirigido, el la licenciatura de un vértice es el número de aristas incidentes a este vértice. En el caso de una gráfica simple tenemos:

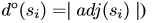
En un gráfico dirigido, el medio grado externo de un vértice es el número de arcos que parten de este vértice. En un gráfico 1 tenemos:

En un gráfico dirigido, el medio grado interior de un vértice es el número de arcos que llegan desde este vértice. En un gráfico 1 tenemos:

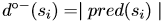
El número de vértices de grado impar es par. La suma de todos los grados es el doble del número de aristas. Dado que la suma de los grados es par y la suma de los grados de los vértices de los grados pares es par, la suma de los grados de los vértices de los grados impares debe ser par. Si la suma de los grados de los vértices con grado impar es par, debe haber un número par de dichos vértices.

Representación informática

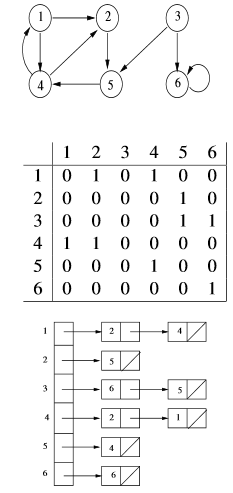
Hay dos formas "académicas" de representar un gráfico en una computadora: mediante una matriz de adyacencia o mediante listas de adyacencia.

Suponemos que los vértices de S están numerados del 1 al no. La matriz de adyacencia es una matriz METRO de tamaño n * n tal que M [i, j] = valor si (i, j) en A, M [i, j] = sin valor de lo contrario. En el marco de la presencia de vínculo entre el vértice i y j, valor = 1 y sin valor = 0. En el marco del vínculo valorado entre el vértice i y j, valor = ponderación y sin valor = infinito. En un marco no orientado, la matriz será simétrica con el triángulo derecho superior. Este tipo de codificación requiere O (| S | ²) ubicaciones de memoria.

La representación por listas de adyacencia consta de una matriz T de no listas, una para cada vértice de S. Una lista enlazada T [s_I] contiene todos los elementos_j de S tal que hay un enlace (s_I, s_j) dentro PARA. Es decir, la lista de sucesores de s_I. Si se valora el gráfico, cada enlace puede contener información sobre la ponderación. Este tipo de codificación requiere ubicaciones de memoria O (| S | + | A |).

Cada método tiene ventajas y desventajas en función de las operaciones que desee realizar en el gráfico.

Caminos

En un grafo dirigido, un camino desde un vértice tu hacia una cumbre v es una secuencia <s₀, s₁,…, S_k> vértices tales que u = s₀ y v = s_k, y (s_I, s_{(yo + 1)}) está en PARA para I de 0 a k-1. La longitud del camino es el número de arcos en el camino, es decir k. Si hay un camino tu Para v, diremos que v es accesible desde tu. Un camino es elemental si los vértices que contiene son todos distintos. u se llama Inicio, v se llama Fin.

Un camino forma un circuito si s₀ = s_k y si el camino tiene al menos un arco. Este circuito es elemental si el camino <s₀,…, S_(k-1)> (el circuito sin el último vértice) es elemental. Por tanto, un bucle es un circuito de longitud 1. Se dice que la gráfica es acíclica si no tiene circuito.

Se dice que un grafo dirigido está fuertemente conectado si cada vértice es accesible desde cualquier otro: para cualquier par de vértices distintos hay una ruta entre ellos.

Esto se puede calcular mediante cierre transitivo. Este último es la suma de no primeras potencias de la matriz de adyacencia, n = | A |. El gráfico está fuertemente conectado si toda la matriz tiene valor. Un componente fuertemente conectado es un subgrafo fuertemente conectado.

Existen las mismas nociones para gráficos no dirigidos bajo el nombre de cadena y ciclo. Se dice que el gráfico está conectado y hablamos de un componente conectado.