Contenido
PalancaColoración gráfica
El problema de la coloración de grafos, para un grafico G no dirigida, consiste en asignar un color a cada vértice de tal manera que no se asigne el mismo color a dos vértices adyacentes.
Cuando el gráfico es plano, esto equivale al problema de colorear un mapa geográfico. El problema de la coloración de gráficos surge en muchas áreas prácticas, como la coincidencia de patrones, planificación deportes, diseño de distribución de asientos, revisión de horarios, programación de taxis y resolución de Sudoku.
El número mínimo de colores necesarios para colorear el gráfico G se denomina número cromático de G y se denota por X (G).
El problema de encontrar el número cromático de una gráfica es un problema Np-completo. El problema de colorear un gráfico con un número limitado de colores: ¿es posible colorear el gráfico con x colores? Si es así, ¿cómo? - también es un problema de Np-completo.
Un gráfico plano es como máximo 4 cromático.
Una cadena es como mucho 2-cromática.
Un ciclo es como mucho 3 cromático.
Una camarilla de tamaño n es n-cromática.
Ejemplo: un conjunto determinado de tareas debe asignarse a intervalos de tiempo, cada tarea requiere solo un intervalo. Las tareas se pueden programar en cualquier orden, pero los pares de tareas pueden entrar en conflicto en el sentido de que no se pueden asignar al mismo intervalo de tiempo, por ejemplo, porque ambos dependen de un recurso compartido. El gráfico correspondiente contiene un vértice para cada trabajo y una ventaja para cada par de trabajos en conflicto. El número cromático del gráfico es exactamente el mínimo requerido, el tiempo óptimo para completar todo el trabajo sin conflictos.
Problema: clics
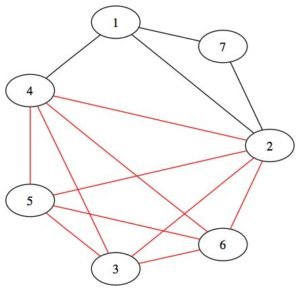
Dado un gráfico G no dirigido, una camarilla es un subconjunto de vértices que están todos conectados en pares por aristas. En otras palabras, es un subgrafo completo.
Encuentra un clic w pedido k en una gráfica es un problema Np-completo.
El siguiente gráfico tiene una camarilla de orden 5:
Problema: estable
Dado un gráfico G no dirigido, un establo es un subconjunto de vértices que no están conectados en pares por aristas. Encontrar un establo de orden k equivale a encontrar una camarilla de orden k en la gráfica inversa, es decir que tiene una arista si no existe en la gráfica original, y viceversa.
Encuentra un establo Para de orden k en una gráfica es un problema Np-completo.
Relación entre los tres problemas y la heurística
Tenemos las siguientes tres propuestas:
- a (G) = w (no G)
- w (G) = a (no G)
- X (G)> = w (G)
Se dice que un S estable de G es máximo por inclusión si no hay un S 'estable de G tal que S esté estrictamente contenido en S'. Una camarilla K es máxima por inclusión si no hay camarillas K 'de G tales que K esté estrictamente contenido en K'.
Por esta definición, deducimos que un estable de orden máximo también es un estable máximo por inclusión, lo contrario no es cierto. La heurística clásica para obtener un establo grande es buscar un establo máximo por inclusión.

El algoritmo de Brélaz es un algoritmo voraz que permite conocer un límite máximo del número cromático de una gráfica. Su principio es simple y procede iterativamente.
Siempre que haya un vértice sin color, elegimos el vértice sin color con el mayor número de vecinos coloreados con diferentes colores. Luego, este vértice se colorea con el color más pequeño posible (los colores se ordenan en un orden ascendente arbitrario). Si todos los colores existentes ya son usados por un vecino, agregamos un nuevo color a nuestra paleta (agregando un color con un valor más alto que todos los demás existentes).
La noción de estable también puede proporcionar indicaciones sobre el color de un gráfico. De hecho, podemos suponer que en un establo, todos los vértices tienen el mismo color. Colorear en k colores equivale a encontrar una partición del conjunto de vértices estables en k.
El algoritmo de Welsh and Powell se basa en esta proposición:
- Ordena los vértices del gráfico en orden decreciente de grado
- Recorriendo la lista en orden, asigne un color no utilizado al primer vértice sin colorear pag, y asigne este color a cada vértice incoloro siguiente de modo que no sea adyacente al vértice pag.
- Regrese a 2 si hay vértices sin color en la lista. De lo contrario, devuelva la lista.
Ejemplo
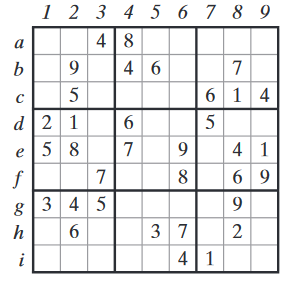
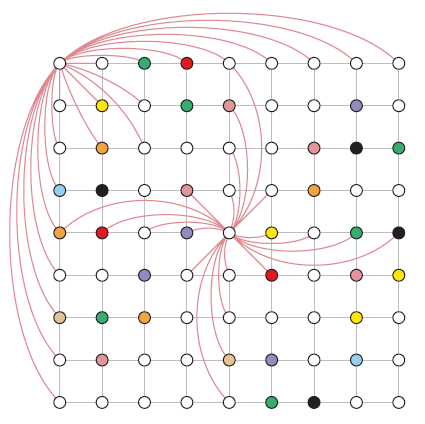
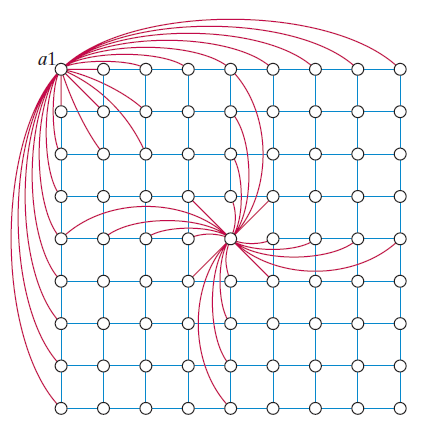
Para ver la conexión entre Sudoku y el coloreado de gráficos, primero describiremos el gráfico de Sudoku, que llamaremos por conveniencia S. El gráfico S tiene 81 vértices, cada vértice representa una celda. Cuando dos celdas no pueden tener el mismo número (ya sea porque están en la misma fila, en la misma columna o en el mismo recuadro), ponemos una arista que conecta los vértices correspondientes del gráfico de Sudoku S.
Por ejemplo, dado que las celdas a3 y a7 están en la misma fila, existe una arista que une sus vértices correspondientes; también hay una arista que conecta a1 y b3 (están en la misma caja), y así sucesivamente. Cada vértice en el gráfico de Sudoku tiene 20 grados y el gráfico tiene un total de 810 aristas. S es demasiado grande para dibujarlo, pero podemos hacernos una idea de la estructura de S mirando un dibujo parcial. El dibujo muestra los 81 vértices de S, pero solo dos (a1 y e5) tienen su conjunto completo de aristas incidentes.
El segundo paso para convertir un Sudoku en un problema de coloración de gráficos es asignar colores a los números del 1 al 9. Esta asignación es arbitraria y no es un orden de prioridad de colores como en el algoritmo.
Una vez que tenemos el gráfico de Sudoku y una asignación de colores a los números del 1 al 9, cualquier Sudoku se puede describir mediante un gráfico de Sudoku donde algunos de los vértices ya están coloreados (los correspondientes a los datos). Para resolver el Sudoku, todo lo que tenemos que hacer es colorear el resto de los vértices usando los nueve colores.