Contenido
PalancaEjercicios corregidos sobre los fundamentos de la teoría de grafos (modelado de grafos y árboles)
Esta página muestra algunos ejercicios corregidos de modelado de gráficos y árboles. El propósito de estos ejercicios es aprender a modelar un problema usando los conceptos y conceptos básicos de Teoría de grafos. La mayoría de los problemas presentados son también simples resolubles con el método clásico.

Ejercicio 1
Dos jugadores tienen 2 o más conjuntos de partidos. Cada turno, el siguiente jugador puede eliminar un cierto número de coincidencias de un lote (dependiendo de la regla elegida). El jugador que quita el último partido pierde.
Modele este juego con un gráfico en el caso de que haya dos pilas, cada una de las cuales contiene tres fósforos, y donde un jugador puede quitar uno o dos fósforos cada uno.
¿Qué movimiento debe hacer el primer jugador para ganar el juego?

El gráfico debe leerse de izquierda a derecha. Un jugador comienza en el nodo 3.3 y cada movimiento toma el camino de un borde a otro nodo. El jugador que llega a 0.0 pierde.
Si el jugador 1 juega, ha ganado si el conjunto de caminos a 0.0 es de tamaño impar, que nunca es el caso, no hay una estrategia ganadora automática.
Ejercicio 2
El siguiente gráfico muestra los pasillos de un museo. Un vigilante situado en un pasillo puede vigilar dos cruces situados en sus extremos. ¿Cuántos guardias se necesitan (y cómo deben colocarse) para que todas las intersecciones estén vigiladas?
Si ahora colocamos guardias en las intersecciones, suponiendo que un guardia pueda monitorear todos los pasillos que conducen a esa intersección, ¿cuántos guardias se necesitan?

Cada guardia se colocará en un borde y podrá monitorear dos intersecciones (vértices). El gráfico tiene 11 vértices; Se necesitarán al menos seis guardias. Por lo tanto, es necesario encontrar un conjunto (mínimo) de al menos seis aristas, tal que cada vértice incida en al menos una de estas aristas. El siguiente gráfico proporciona una solución (bordes más gruesos).
Esta vez, los guardias están en las cimas y observan las crestas. Debe haber un conjunto de vértices tal que cada arista incida en al menos uno de estos vértices. El siguiente gráfico proporciona una solución utilizando 6 vértices (vértices blancos).

Ejercicio 3
Skynet es una red de 15 vértices. Puede pasar de cada vértice a al menos otros siete vértices por enlace. ¿Podemos ir por enlace desde un vértice X a cada uno de los otros?
Sea A cualquier vértice. X está vinculado a al menos 7 ciudades diferentes. Entonces tenemos una red de 8 vértices conectados por enlaces. Dentro de un vértice, también puede conectarse con al menos otros siete vértices; entonces hay una nueva red de 8 vértices. Debe haber un vértice compartido en estas redes, de lo contrario la red tendría al menos 16 vértices. X está conectado a A en dos planos como máximo, por este vértice común; está conectado con todas las demás ciudades.
Ejercicio 4
Una red está formada por siete fábricas. Una ciudad está vinculada a exactamente dos fábricas. Dos fábricas comparten exactamente una ciudad. ¿Cuántas ciudades son servidas por la red?
Las fábricas son los vértices y las ciudades están representadas por una arista que conecta dos vértices. La regla 2 implica que no hay aristas múltiples y que cualquier par de vértices son adyacentes; es decir, el gráfico está completo; es K7, o 21 enlaces.
Ejercicio 5
Considerémoslo programa lineal Próximo :

Donde X es 0 o 1. Determinar, con un problema gráfico, una solución que maximice la función objetivo (suma de las X).
Un vértice representa una variable. Dos vértices están conectados si están en la misma desigualdad. El problema es encontrar un conjunto máximo de vértices donde ningún par de vértices tenga un enlace directo.

Ejercicio 6
Considerando un conjunto de fichas de dominó utilizando los números 0, 1, 2, 3, 4, ya que cada ficha de dominó consta de dos dígitos distintos, como son el 1 y el 3, se plantea el siguiente problema: ¿es posible alinear todas las fichas de modo que cuando dos peones "tocan" los números "en contacto" son idénticos?
Muestre el problema como un gráfico completo K5. El problema es encontrar un ciclo euleriano en el gráfico.

Ejercicio 7
En un grupo de personas, siempre hay dos individuos que conocen exactamente el mismo número de miembros del grupo. Demuestra esto.
Debemos probar que en un grafo simple (sin dobles aristas, sin bucles), siempre hay dos vértices que tienen el mismo grado. Razonaremos por absurdo y supondremos que existe un grafo simple con n vértices del cual todos los grados son diferentes. Entonces los grados de los vértices están entre 0 y n−1, y por lo tanto si todos los grados son diferentes, como tenemos n vértices y simplemente n posibilidades para los grados, todas estas posibilidades deben tomarse.
En particular, debe haber un vértice de grado 0 y un vértice de grado n−1. Pero es imposible, porque este último vértice debería tener una arista hacia todos los demás, y no es posible ya que un vértice es de grado 0, por lo tanto aislado.
Ejercicio 8
Sea G un grafo simple no dirigido de orden 2p (número de aristas). Suponemos que el grado de cada vértice es al menos igual a p. Demuestra que esta gráfica es conexa.
Supongamos por absurdo que este grafo no es conexo, y sean x,y dos vértices tales que no hay camino que una x con y. Entonces, x tiene al menos p vecinos, al igual que y. Pero los vecinos de x son todos necesariamente distintos de los vecinos de y: de lo contrario, existiría una cadena de longitud 2 que une x con y.
Por lo tanto, el gráfico incluye al menos 1+1+p+p=2p+2 vértices (x, y, los vecinos de x, los vecinos de y). Obtenemos por tanto una contradicción ya que la gráfica es de orden 2p.
Ejercicio 9
Una cabra, un repollo y un lobo están en la orilla de un río; un contrabandista desea transportarlos a la otra orilla pero, como su bote es demasiado pequeño, solo puede transportar uno de ellos a la vez. ¿Cómo debe proceder para no dejar nunca al lobo y la cabra, oa la cabra y la col, juntos y desatendidos?
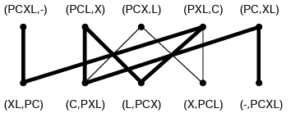
Esta situación se puede modelar usando un gráfico. Designemos por P al barquero, por C a la cabra, por X al repollo y por L al lobo. Los vértices del gráfico son pares que especifican quién está en el borde inicial, quién está en el otro borde.
Así, la pareja (PCX,L) significa que el barquero está en la orilla inicial con la cabra y el repollo (que por lo tanto están bajo vigilancia), mientras que el lobo está en la otra orilla. Una arista conecta dos vértices cuando el colocador puede pasar de una situación a otra.
Al transportar la cabra, el barquero pasa, por ejemplo, de la cima (PCX,L) a la cima (X,PCL). El grafo así obtenido es bipartito: los vértices para los que el colocador está en la orilla inicial sólo están conectados con los vértices para los que el colocador está en la otra orilla.
Naturalmente, no consideraremos los vértices de cuál de los componentes es CX o LC porque estas situaciones están prohibidas. Entonces es suficiente encontrar un camino (el más corto por ejemplo) entre la situación inicial (PCXL,-) y la situación final deseada (-,PCXL). La siguiente figura da tal camino:
Ejercicio 10
En el siguiente gráfico bipartito, los vértices T1,..., T6 representan trabajadores y los vértices E1,..., E6 puestos de trabajo. Un borde conecta a un trabajador con un trabajo si el trabajador tiene las calificaciones para ese trabajo. ¿Cómo asignar puestos de trabajo a los trabajadores para minimizar el número de desempleados?
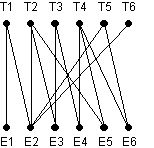
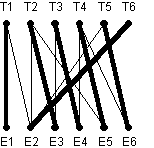
Asignar un trabajo a una persona es como "seleccionar" un borde. Cada persona solo puede tener un trabajo, y un trabajo solo puede ser realizado por una persona, por lo que es necesario seleccionar un número máximo de aristas de tal manera que estas aristas no tengan un vértice común (este conjunto se denomina máximo estable) .
Ejercicio 11
Todos los días, un grupo de 12 niños sale a caminar, en filas de dos. ¿Cuántos días pueden salir a pasear si no queremos que un niño tenga dos veces al mismo vecino? ¿Y si ahora el paseo se hace en filas de tres?
Considere el gráfico completo K12 con 12 vértices, cada vértice representa a un niño. El número de aristas en este gráfico es 12 x 11 / 2 = 66. Un paseo corresponde a un conjunto de 6 aristas no incidentes (que no tienen vértice en común): cada arista representa una fila (dos niños) y cada niño solo puede pertenecen a una fila durante un viaje.
Por tanto, es necesario encontrar el mayor número de conjuntos (11 = 66/6) respetando esta regla:
1-2, 3-12, 4-11, 5-10, 6-9, 7-8 ; 2-3, 12-4, 11-5, 10-6, 9-7, 8-1 ; 1-3, 4-2, 5-12, 6-11, 7-10, 8-9 ; 3-4, 2-5, 12-6, 11-7, 10-8, 9-1 ; 1-4, 5-3, 6-2, 7-12, 8-11, 9-10 ; 4-5, 3-6, 2-7, 12-8, 11-9, 10-1 ; 1-5, 6-4, 7-3, 8-2, 9-12, 10-11 ; 5-6, 4-7, 3-8, 2-9, 12-10, 11-1 ; 1-6, 7-5, 8-4, 9-3, 10-2, 11-12 ; 6-7, 5-8, 4-9, 3-10, 2-11, 12-1 ; 1-7, 2-12, 3-11, 4-10, 5-9, 6-8
Ejercicio 12
Estamos interesados en grafos en los que todos los vértices son de grado tres. Construya tales gráficos que tengan 4 vértices, 5 vértices, 6 vértices, 7 vértices. ¿Qué deduces de esto?
Los gráficos con todos los vértices de grado tres se llaman gráficos 3-regulares o gráficos cúbicos. La siguiente figura muestra dos gráficos cúbicos, que tienen 4 y 6 vértices respectivamente. De hecho, es fácil ver que no hay gráficos cúbicos con un número impar de vértices: el número de aristas de un gráfico cúbico con n vértices es 3n/2, que es solo un número entero cuando n es par.

Ejercicio 13
Un servidor puede enrutar un máximo de paquetes al mismo tiempo. Siete subestaciones están vinculadas a un servidor, una subestación no puede enviar paquetes si algunas subestaciones ya están utilizando el enlace. La siguiente tabla muestra la capacidad de cada subestación para enviar un paquete en relación con las demás. Por ejemplo, un paquete de A no se puede enviar si ya hay un paquete de D, pero se puede enviar cuando B ha enviado un paquete.
Subestación | PARA | B | VS | D | mi | F | GRAMO |
no esta con | DE | D, E, F, G | P.EJ | A, B, E | A, B, C, D, F, G | B, E, G | B, C, E, F |
Representar los enlaces en un gráfico. ¿Cuántos paquetes debe manejar el servidor al mismo tiempo (valor máximo)?
Ejercicio 14
Una escuela debe pasar pruebas escritas a cuatro estudiantes: Pierre, Jean, Guillermo e Ibrahim. Siete disciplinas están involucradas: Matemáticas, física, biología, francés, inglés, español e historia.
Pierre debe aprobar matemáticas, física e inglés, Jean matemáticas, biología y francés, Guillermo matemáticas, inglés y español e Ibrahim física, francés e historia.
¿Cuál es el número mínimo de franjas horarias que se deben proporcionar para que ningún alumno tenga que realizar dos pruebas simultáneamente? ¿Cuál es el número cromático de un grafo completo? ¿Cómo enlazar números cromáticos en un gráfico?
Un vértice representa una disciplina, un borde conecta dos disciplinas si no pueden tener lugar al mismo tiempo. El problema se puede resolver buscando un número mínimo de colores. El subgrafo completo más grande es K3, por lo que hay al menos 3 colores. El grado máximo es cinco, por lo que hay como máximo 5 colores. Por experimento, el gráfico es tricromático.

Ejercicio 15
El siguiente diagrama representa una encrucijada.

Cada ramal tiene su propio semáforo con indicación de flecha de la dirección autorizada, y aquí están los posibles cruces de este cruce.

Los automóviles con luz verde no deben cruzarse, por lo que no se pueden autorizar AC y BE simultáneamente.
Proponer una solución que permita alternar la autorización de semáforos en esta intersección.
El gráfico que modela la encrucijada se muestra a continuación. Su número cromático es igual a 4 (es de 4 colores y contiene un K4 que agrupa los vértices AC, BD, CD y DA). Un conjunto de vértices del mismo color, por ejemplo ED, AC, AE y CA agrupa un conjunto de caminos que se pueden realizar al mismo tiempo (sin incompatibilidad).
El número cromático corresponde entonces al número mínimo de "ciclos" que deben respetar los semáforos de este cruce.
Para nuestro ejemplo tendremos: 1. ED, AC, AE y CA 2. BA, BE, BD y EC 3. DC y DA 4. CD. Por supuesto, son posibles otras soluciones (cuatro colores).

Ejercicio 16
Considere un gráfico no dirigido con vértices. Demostrar que todas las siguientes propiedades son equivalentes:
- es un árbol
- es conexo y si quitamos una arista, el grafo ya no es conexo
- está conectado con n-1 aristas
- no tiene ciclo hasta que agregamos un borde
- no tiene ciclo con borde n-1
- un solo camino entre cualquier par de vértices
¡No hay solución ya que está en el curso de los árboles!
Ejercicio 17
Queremos agregar una granja en una red. El siguiente gráfico muestra el costo de enviar energía entre dos subestaciones de la red y la cantidad de energía enviada por una subestación. Debe colocar la batería en una subestación mientras minimiza el costo total.

Calcule la suma de todos los costos en cada subestación, es decir, el costo de cada ruta entre cualquier subestación y la subestación elegida (borde * vértice).

Ejercicio 18
Vamos a ver un principio muy importante en la teoría de grafos (relacionado con temas sociales) que es la centralidad (hay mucho cálculo de centralidad).
Un robot camina sobre el siguiente gráfico. Partiendo de cualquier vértice s, llamado vértice de almacenamiento, debe dejar caer un cubo en cada uno de los otros vértices. Tiene suficientes cubos en el vértice de almacenamiento, pero solo puede transportar un cubo a la vez (por lo que debe pasar por el vértice de almacenamiento antes de entregar otro cubo).
Calcula, para cada uno de los vértices del gráfico, el camino mínimo que debe recorrer el robot si este vértice es un vértice de almacenamiento. ¿Cuál es el "mejor" vértice de almacenamiento?
Para un vértice dado, es necesario calcular la suma de las longitudes de los caminos más cortos desde este vértice a los otros vértices (fácil ya que estamos tratando con casi un árbol). La siguiente figura da este valor para el vértice A, luego para todos los vértices del gráfico. Por lo tanto, el mejor vértice de almacenamiento es el vértice X.

Ejercicio 19
La puesta en marcha de un nuevo yacimiento minero requiere la realización de un determinado número de tareas. La siguiente tabla representa estas diferentes tareas con sus relaciones de anterioridad.

Un vértice de un gráfico de programación contiene 3 elementos:
- El nombre de la tarea, la hora de finalización más temprana y la hora de finalización más tardía.
- Un arco muestra la dependencia de una tarea respecto a otra con una ponderación del número de días de la tarea anterior. Entonces A y B están vinculados con un peso de 120.
(en lugar de un arco, también es posible hacer un gráfico jerárquico, es decir, el vértice más alto es la raíz, sus sucesores directos están en la siguiente altura).
Un vértice delgado está relacionado con tareas sin sucesor.
El tiempo de finalización más temprano es el camino más largo de una tarea a otra en el sentido de la jerarquía.
El último tiempo de finalización es la ruta más corta en la dirección opuesta de la jerarquía.
El camino crítico es el camino desde la primera tarea hasta el final cuyos tiempos más tempranos y últimos coinciden.
Construya el gráfico de programación.
Al usar el Método MPM, obtenemos el siguiente gráfico. Las fechas más tempranas y más tardías se calculan "por niveles". Las tareas críticas y la ruta crítica se indican en negrita. El tiempo mínimo de finalización del conjunto se puede leer en la parte superior FIN: 1170 días.

Ejercicio 20
Un grupo de 9 alumnos se reúne todos los días en torno a una mesa redonda. ¿Cuántos días pueden encontrarse si no queremos que ninguno tenga dos veces el mismo vecino?
Denotemos por 1,2,…,9 las 9 personas y consideremos el grafo completo K9 con 9 vértices. Una composición de la tabla corresponde a un ciclo. hamiltoniano de K9 (un ciclo que pasa una y sólo una vez por cada vértice).
Si dos composiciones de mesa corresponden a dos ciclos que tienen un borde común, significa que las dos personas conectadas por este borde se encuentran una al lado de la otra. Así, el problema consiste en determinar el número de ciclos hamiltonianos disjuntos de K9.
El gráfico K9 tiene 9 x 8 / 2 = 36 aristas y cada ciclo usa 9 aristas, este número es como máximo igual a 4… Es efectivamente igual a 4, como lo demuestran los siguientes 4 ciclos hamiltonianos disjuntos:
1,2,3,9,4,8,5,7,6 — 1,3,4,2,5,9,6,8,7 — 1,4,5,3,6,1,7, 9.8 — 1.5,6,4,7,2,8,1.9
Ejercicio 21
En esta ocasión, estas reuniones diarias se refieren a un grupo de 12 alumnos, 6 chicas y 6 chicos. Siempre queremos que nadie tenga dos veces al mismo vecino, pero esta vez también queremos que cada chica esté rodeada de dos chicos. ¿Cuántos días se pueden encontrar?
La idea básica es la misma que en el ejercicio anterior, pero esta vez, debido a la alternancia impuesta entre niña y niño, razonamos sobre el grafo bipartito completo K6,6 (seis niñas y seis niños).
Este gráfico incluye 6 x 6 = 36 aristas, y cada ciclo hamiltoniano requiere 12 de ellas, por lo que hay como máximo 3 soluciones. De hecho, son posibles tres soluciones (fi representa a la i-ésima niña, gi al i-ésimo niño), por ejemplo:
(f1,g1,f2,g2,f3,g3,f4,g4,f5,g5,f6,g6) — (f1,g3,f2,g4,f3,g5,f4,g6,f5,g1,f6,g2 ) —
(f1,g5,f2,g6,f3,g1,f4,g2,f5,g3,f6,g4)
Ejercicio 22
Un grupo de ocho personas se reúnen para cenar. El gráfico de al lado especifica las “incompatibilidades de humor” entre las personas de este grupo (un borde que conecta a dos personas indica que se llevan muy moderadamente…).

Proponga un plan de asientos (la mesa es redonda) para este grupo, evitando colocar a dos personas “incompatibles” una al lado de la otra.
Esta vez se trata de encontrar ciclos hamiltonianos en el complemento de la gráfica. Aquí hay uno: B,C,H,A,F,G,E,D.

