Contenido
PalancaProyecto de teoría de grafos: Sim City 2030
Este proyecto sobre el Teoría de grafos, la programación lineal, branch & bind y problemas de flujo es una introducción a los problemas de redes inteligentes.

Hola queridos ingenieros de NE,
Su equipo ha ganado con éxito el proyecto Sim City 2030. Nuestro alcalde, el venerable Frédéric Fauberteau (puedes llamarlo dios) y sus cuatro asesores Guillaume Guérard (el uno, el único), Pascal Clain (¿Qué otra cosa?), Samir Yahiaoui (serás derribado) y Marie-Noémie Thai (nuestra diosa) te han elegido para construir la planta de paneles solares más grande de la región:
¡Muere Sonne!
Su trabajo, que enviará en forma de entregables, se centrará en los siguientes temas:
- Definir dónde construir la planta. (Sesión 1)
- Definir necesidades energéticas (Sesión 2)
- Configurar el plan de integración de la central eléctrica y una nueva línea eléctrica(Sesión 3)
Entregable 1: ¿dónde construir la planta?
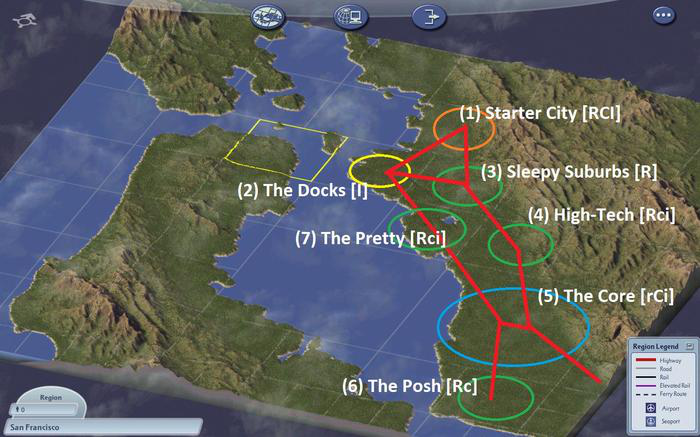
Starter City está ubicada en una aglomeración de tres ciudades (con The Docks y The Core), servidas por tres plantas de energía cercanas (Sleepy Suburbs, The Pretty y The Posh).
Antes de integrar la planta del proyecto Die Sonne en la red local, es necesario conocer su ubicación. Para ello, los meteorólogos colocaron sensores con el fin de conocer el poder activo de varios sitios en el sitio de Alta Tecnología de Simicon Valley y dedujeron varias ubicaciones favorables de él.
La construcción de la planta de energía tiene un costo y la instalación de líneas eléctricas al transformador más cercano también tiene un costo.
Antes de comenzar con este primer entregable, lo invito a conocer los conceptos básicos de la teoría de grafos.
Ahora que se ha familiarizado con la noción de gráfico, vamos a probar un primer método para saber dónde construir la planta.
El gráfico es el siguiente con A, B, C las tres posibilidades de construcción, el costo de las centrales es el mismo, lo descuidaremos más adelante. Los nodos D y E son estaciones de transmisión y el nodo F es la estación que ya existe en la red. El objetivo, por tanto, es encontrar dónde colocar la planta (A, B o C) de forma que se minimice el coste de las líneas desde este vértice hasta F.
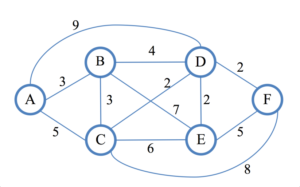
Para saber el camino más corto de A a F, construirás un árbol de decisión En profundidad 0 está tu central: nodo A.
En cada profundidad, para cada nodo de la profundidad anterior, encontrará todos los caminos a los vértices adyacentes que no forman parte de sus padres. Si una rama que termina en el vértice X tiene una ruta más corta que otra rama que termina en X, entonces no es necesario hacer el cálculo para la rama con una ruta más grande, el vértice está cerrado.
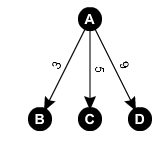
Comencemos a construir el árbol de decisión de A. El vértice A puede ir a B en 3, C en 5 y D en 9. Esto da el siguiente árbol.
Luego tomamos la profundidad 1 y comenzamos el proceso nuevamente con B luego C luego D.
Aquí B puede ir a D en 4, en E en 7, en C en 3 y en A en 3. A es uno de los padres de B (siga los arcos que van en dirección contraria). En este ejemplo, solo haremos los cálculos para la rama A a la B.
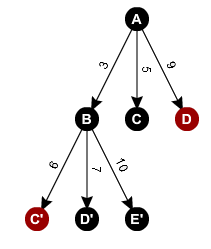
Para cada camino, agregamos el arco del padre con el arco del hijo. Aquí de B a D tendremos 3 + 4, a E tendremos 3 + 7 y a C tendremos 3 + 3.
Observamos que la rama A a la B a la D tiene un costo de 3 + 4 = 7, por lo que podemos cerrar la rama A a la D. La rama A a la B a C tiene un costo de 3 + 7 = 10 que es mayor que la rama A a C, que tiene un costo de 5. Por lo tanto, podemos cerrar la rama A de la B a la C. En esta etapa, ya hemos cerrado dos ramas de nuestro árbol de decisión (en rojo en el árbol).
Atención, si continúa en la rama A a la B a la D, tendrá a A y B como padres.
Completa el árbol de decisiones de rama y límite. El camino más corto de A a F será la rama que va a F de manera que F no esté cerrada.
Felicidades ! Acabas de hacer tu primera algoritmo optimización: Rama & Bound! Todo lo que queda es codificar.
Las computadoras son siempre más rápidas que los humanos, por lo que es necesario codificar un algoritmo de árbol de decisiones. Agregar rama y límite (cerrar nodos innecesarios) proporcionará puntos de bonificación. En su programa, cada nodo tendrá como información:
- El peso de su camino
- El nodo visitado en curso
- Los nodos a visitar (que por tanto serán hijos directos)
- ¿Pertenece al camino más corto de B (luego C) a F que calculará después de crear el árbol?
¿Qué ubicación tendrá el menor costo de construcción de las líneas? ¿Mostrar prueba mostrando los árboles de decisión que muestra su programa?
Escala
- Rama y límite (10 puntos)
- Escritura de árbol (2 puntos)
- Marque los nodos cerrados (3 puntos)
- Marque el camino más corto (3 puntos)
- Conclusión (2 puntos)
- Código del árbol de decisión (10 puntos)
- diagrama de flujo del algoritmo (3 puntos)
- Explicación del proceso (3 puntos)
- Impresión de pantalla de la visualización del árbol de decisiones (2 puntos)
- Marque el camino más corto (2 puntos)
- BONUS cierra nodos innecesarios (2 puntos)
Producto previsto 2: ¿Cuáles son las necesidades energéticas?
Para conocer las necesidades energéticas, debemos establecer el encaminamiento de la energía de las plantas existentes hacia las ciudades de la aglomeración. Este enrutamiento determinará que efectivamente sea un problema de producción de energía y no un problema a nivel de distribución.
Sabemos que la planta 1 produce un máximo de 6 MWh, la planta 2 produce un máximo de 10 MWh y la planta 3 produce un máximo de 6 MWh. La ciudad 1 (Starter City) consume 12MWh, la ciudad 2 (The Core) consume 10 MWh, la ciudad 3 (The Docks) consume 3MWh.
La energía se conduce desde las centrales a las ciudades mediante líneas de media tensión según el siguiente diagrama (Ci para las centrales y Vi para las ciudades).
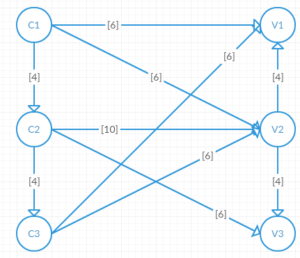
Entre corchetes tienes la capacidad de la línea en MWh.
Para conocer las necesidades energéticas, es necesario resolver un problema de flujo.
Por lo tanto, primero debe transformar el gráfico anterior en un flujo, es decir, con una sola fuente y un solo pozo. Cree una fuente madre que estará conectada a cada planta y que tendrá una capacidad igual a la producción de las plantas (por ejemplo, Fuente Para C1 tendrá una capacidad de 6). Así mismo, conectarás bien cada ciudad al padre, la capacidad de cada arco será igual al consumo de la ciudad en cuestión.
Construya el gráfico asociado y resuelva el problema de flujo con la ayuda del algoritmo de Ford-Fulkerson.
Cuál es el flujo maximo ? ¿Cuánto necesitan las ciudades? ¿Cuántos MWh debe producir la planta de energía solar?
Te has vuelto profesional en mejoramiento ! Ahora vamos a ver un poco de automatización.
La estación de energía solar está conectada a baterías. Cuando la energía producida por la planta no es útil para cubrir el consumo, la energía se almacena. Para automatizar el proceso, el almacenamiento y la recuperación de la batería se realizará únicamente a través de un circuito electrónico.
Necesita modelar este proceso usando un circuito y un arduino. Un servomotor representará a los consumidores, y los LED deberán encenderse según el flujo que pase por la línea. La energía producida por la planta de energía en el circuito dependerá de un fotorresistor.
Usando un servomotor, un fotoresistor, LED y el arduino, cree un diagrama para modelar el sistema. El diagrama debe hacerse con http://fritzing.org/
Escala
- Problema de flujo (10 puntos)
- Construcción del gráfico (3 puntos)
- Ejecución del algoritmo -al menos dos iteraciones- (5 puntos)
- Conclusión (2 puntos)
- Diagrama electrónico (10 puntos)
- Explicación del diagrama (5 puntos)
- Diagrama de Fritzing (4 puntos)
- Relevancia y sencillez del modelo (1 puntos)
Producto final 3: inteligencia artificial versus deducción humana
Ha determinado en el entregable 1 el costo de la línea para la nueva unidad de control. Esta línea irá desde la nueva planta hasta la planta C1. Y determinó en el entregable 2 que esta planta de energía solar tendrá que producir 3 MWh. Ahora verá si la integración de esta planta resolverá nuestro problema de sobreconsumo y determinará la capacidad de la nueva línea.
Es trivial que la nueva línea tenga una capacidad de 3MWh ya que es el único arco que sale de la nueva planta. Pasemos por alto este hecho, la idea es probar las cosas, no deducirlas.
Para validar su dimensionamiento, agregará un vértice C4 y un arco de C4 a C1 de capacidad infinita. Una vez que haya determinado el gráfico, realice el algoritmo de Ford-Fulkerson. Tendrás dos posibilidades:
- Si se satisface la demanda, entonces el flujo que pasa por el arco (C4, C3) determina la capacidad necesaria de la línea.
- Si no se satisface la demanda, se debe determinar qué líneas están impidiendo que se entregue más energía.
¿Cuándo se deduce por la nueva línea?
¡Ahora pongámonos manos a la obra!

Te espera una última tarea. Necesita determinar el impacto que el ataque de Bowser puede tener en la Red de Nueva Energía.
Realice el enrutamiento considerando que el arco (C2, V2) está cortado. Para comprender las consecuencias de esta ruptura en la red, debe realizar el corte mínimo.
El corte mínimo se realiza después de encontrar un flujo máximo con Ford-Fulkerson.
Este corte permitirá entender que serán las próximas líneas las que estarán en congestión.
¿Qué deduces de esto?
Nada supera a un ejemplo de un conjunto electrónico que representa la red con la ayuda de LED para mostrar el flujo y las resistencias para que el flujo sea idéntico a sus cálculos. Tenga cuidado, tiene muchos cálculos que hacer, ¡incluidos los puentes divisores de voltaje!
La eliminación de un cable mostrará el impacto en la red (esto es cierto en el momento del corte, posteriormente la red se reajusta).
Qué observa ?
Escala
- Tamaño de línea (7 puntos)
- Escribir la gráfica (3 puntos)
- Cálculo del caudal máximo (3 puntos)
- Conclusión (1 puntos)
- Salto de línea (7 puntos)
- Cálculo del caudal máximo (3 puntos)
- Hallar el min-corte (3 puntos)
- Conclusión (1 puntos)
- Montaje Arduino (7 puntos)
- Cálculo de resistencias (5 puntos)
- Diagrama de Fritzing (1 puntos)
- Conclusión (1 puntos)
