Contenus
ToggleProjet de théorie des graphes : Sim City 2030
Ce projet sur la théorie des graphes, la programmation linéaire, le branch & bound et les problèmes de flots est une introduction aux problèmes liés au smart grid.

Bonjour chers ingénieurs NE,
Votre équipe a remporté avec succès le projet Sim City 2030. Notre maire, le vénérable Frédéric Fauberteau (vous pouvez l’appeler dieu) et ses quatre conseillers Guillaume Guérard (le seul, l’unique), Pascal Clain (what else ?), Samir Yahiaoui (vous serez renversé) et Marie-Noémie Thai (notre déesse) vous ont choisi pour construire la plus grande centrale de panneaux solaires de la région :
Die Sonne !
Vos travaux, que vous rendrez sous la forme de Livrables, porteront sur les sujets suivants :
- Définir où construire la centrale (Séance 1)
- Définir les besoins énergétiques (Séance 2)
- Mettre en place le plan d’intégration de la centrale et d’une nouvelle ligne électrique(Séance 3)
Livrable 1 : où construire la centrale ?
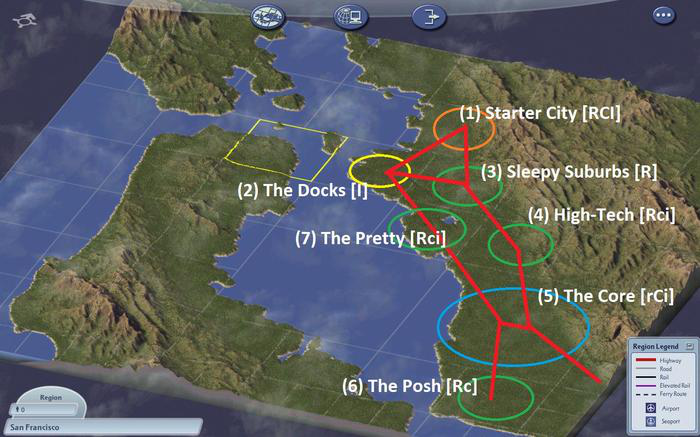
La ville Starter City est située dans un agglomérat de trois villes (avec The Docks et The Core), desservies par trois centrales de proximité (Sleepy Suburbs, The Pretty et The Posh).
Avant d’intégrer la centrale du projet Die Sonne dans le réseau local, il vous faut connaitre son emplacement. Pour cela, les météorologues ont placés des capteurs afin de connaître la puissance active de divers sites dans le site High-Tech de la Simicon Valley et en ont déduit divers emplacement favorables.
La construction de la centrale a un cout et la mise en place des lignes électriques vers le transformateur le plus proche a aussi un coût.
Avant de commencer ce premier livrable, je vous invite à prendre connaissance des bases de la théorie des graphes.
Maintenant que vous vous êtes familiarisé avec la notion de graphe, nous allons essayer une première méthode pour savoir où construire la centrale.
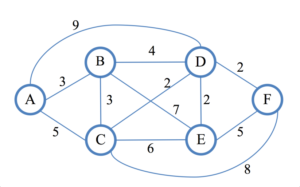
Le graphe est le suivant avec A, B, C les trois possibilités de construction, le coût des centrales est le même, on le négligera par la suite. Les nœuds D et E sont des postes de transmission et le nœud F est le poste déjà existant dans le réseau. L’objectif est donc de trouver où placer la centrale (A, B ou C) de telle façon à minimiser le coût des lignes de ce sommet vers F.
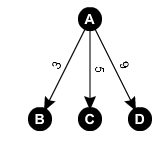
Afin de connaître le plus court chemin de A vers F, vous allez construire un arbre de décision. En profondeur 0 se trouve votre centrale : le nœud A.
A chaque profondeur, pour chaque nœud de la profondeur précédente, vous allez trouver tous les chemins vers les sommets adjacents qui ne font pas partie de ses parents. Si une branche se terminant par le sommet X a un chemin plus court qu’une autre branche se terminant par X, alors il n’est pas nécessaire de faire le calcul pour la branche avec un chemin plus grand, le sommet est fermé.
Commençons à établir l’arbre de décision de A. Le sommet A peut aller à B en 3, à C en 5 et à D en 9. Ce qui donne l’arbre suivant.
Puis nous prenons la profondeur 1 et nous recommençons le processus avec B puis C puis D.
Ici B peut aller en D en 4, en E en 7, en C en 3 et en A en 3. A fait partie des parents de B (suivre les arcs en remontant à contre sens). Dans cet exemple nous ne ferons les calculs que pour la branche A à B.
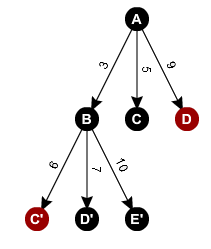
Pour chaque chemin, nous additionnons l’arc du parent avec l’arc de l’enfant. Ici pour B vers D nous aurons 3+4, vers E nous aurons 3+7 et vers C nous aurons 3+3.
Nous remarquons que la branche A à B à D à un cout de 3+4=7, nous pouvons donc fermer la branche A à D. La branche A à B à C a un cout de 3+7=10 qui est supérieur à la branche A à C qui a un cout de 5. Nous pouvons donc fermer la branche A à B à C. A ce stade, nous avons déjà fermé deux branches de notre arbre de décision (en rouge dans l’arbre).
Attention, si vous continuez sur la branche A à B à D vous aurez alors A et B comme parents.
Complétez l’arbre de décision du branch & bound. Le plus court chemin de A vers F sera la branche allant vers F telle que F ne soit pas fermé.
Félicitation ! Vous venez de faire votre premier algorithme d’optimisation : le Branch & Bound ! Il ne reste plus qu’à coder.
L’ordinateur est toujours plus rapide que l’humain, c’est pourquoi il vous faut coder un algorithme d’arbre de décision. L’ajout du branch & bound (le fait de fermer les nœuds non utiles) fournira des points bonus. Dans votre programme, chaque nœud aura pour information :
- Le poids de son chemin
- Le nœud visité en cours
- Les nœuds à visiter (qui seront donc des fils directs)
- L’appartenance au plus court chemin de B (puis C) à F que vous calculerez après la création de l’arbre ?
Quel emplacement aura le cout de construction des lignes la plus faible ? Montrer la preuve en affichant les arbres de décision que votre programme affiche ?
Barème
- Branch & bound (10 points)
- Ecriture de l’arbre (2 points)
- Marquer les nœuds fermés (3 points)
- Marquer le plus court chemin (3 points)
- Conclusion (2 points)
- Code de l’arbre de décision (10 points)
- Logigramme de l’algorithme (3 points)
- Explication du processus (3 points)
- Impression écran de l’affichage de l’arbre de décision (2 points)
- Marquer le plus court chemin (2 points)
- BONUS fermer les nœuds non utiles (2 points)
Livrable 2 : Quelles sont les besoins énergétiques ?
Afin de connaître les besoins énergétiques, nous devons établir le routage de l’énergie des centrales existantes vers les villes de l’agglomérat. Ce routage va déterminer qu’il s’agit bien d’un problème de production énergétique et non d’un problème au niveau de la distribution.
Nous savons que la centrale 1 produit au maximum 6 MWh, la centrale 2 produit au maximum 10 MWh et la centrale 3 produit au maximum 6 MWh. La ville 1 (Starter City) consomme 12MWh, la ville 2 (The Core) consomme 10 MWh, la ville 3 (The Docks) consomme 3MWh.
L’énergie est conduite des centrales vers les villes par des lignes moyennes tensions selon le schéma suivant (Ci pour les centrales et Vi pour les villes).
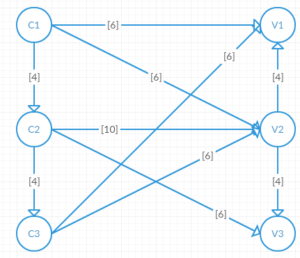
Entre crochets vous avez la capacité de la ligne en MWh.
Afin de connaître les besoins énergétiques, vous avez besoin de résoudre un problème de flot.
Vous devez donc dans un premier temps transformer le graphe ci-dessus en flot, c’est-à-dire avec une seule source et un seul puit. Créez une source mère qui sera relié à chaque centrale et ayant une capacité égale à la production des centrales (par exemple Source à C1 aura une capacité de 6). De même, vous relierez chaque ville au puit père, la capacité de chaque arc sera égale à la consommation de la ville en question.
Construisez le graphe associé et résolvez le problème de flot avec l’aide de l’algorithme de Ford-Fulkerson.
Quel est le flot maximum ? De combien ont besoin les villes ? Combien la centrale solaire doit-elle produire de MWh ?
Vous êtes devenu des pros en optimisation ! Maintenant on va voir un peu d’automatisme.
La centrale solaire est rattachée à des batteries. Lorsque l’énergie produite par la centrale n’est pas utile pour satisfaire la consommation, l’énergie est alors stockée. Afin d’automatiser le processus, le stockage et le déstockage de la batterie se fera uniquement via un circuit électronique.
Vous devez modéliser ce processus à l’aide d’un circuit et d’une arduino. Un servomoteur représentera les consommateurs, et des LED devront s’éclairer en fonction du flot passant dans la ligne. L’énergie produite par la centrale dans le circuit dépendra d’une photorésistance.
A l’aide d’un servomoteur, d’une photorésistance, de LED et de l’arduino, proposez un schéma permettant de modéliser le système. Le schéma devra être fait avec http://fritzing.org/
Barème
- Problème de flot (10 points)
- Construction du graphe (3 points)
- Exécution de l’algorithme -au moins deux itérations- (5 points)
- Conclusion (2 points)
- Schéma électronique (10 points)
- Explication du schéma (5 points)
- Schéma Fritzing (4 points)
- Pertinence et simplicité du modèle (1 points)
Livrable 3 : intelligence artificielle versus déduction humaine
Vous avez déterminé dans le livrable 1 le cout de la ligne pour la nouvelle centrale. Cette ligne ira de la nouvelle centrale vers la centrale C1. Et vous avez déterminé dans le livrable 2 que cette centrale solaire devra produire 3 MWh. Vous allez maintenant regarder si l’intégration de cette centrale réglera notre problème de surconsommation, et déterminer la capacité de la nouvelle ligne.
Il est trivial que la nouvelle ligne aura une capacité de 3MWh puisque c’est le seul arc sortant de la nouvelle centrale. Passons sur ce fait, l’idée est de prouver les choses, pas les déduire.
Afin de valider votre dimensionnement, vous allez rajouter un sommet C4 et un arc de C4 vers C1 de capacité infini. Une fois que vous aurez déterminé le graphe, effectuez l’algorithme de Ford-Fulkerson. Vous aurez deux possibilités :
- Si la demande est satisfaite, alors le flot passant par l’arc (C4, C3) détermine la capacité nécessaire de la ligne
- Si la demande n’est pas satisfaite, alors il faut déterminer quelles lignes empêchent de délivrer plus d’énergie.
Quand déduisez-vous pour la nouvelle ligne ?
Maintenant on va passer aux choses sérieuses !

Une dernière tache vous attend. Vous devez déterminer l’impact que peut avoir une attaque de Bowser sur le nouveau réseau énergétique.
Effectuer le routage en considérant que l’arc (C2, V2) est coupé. Afin de comprendre les conséquences de cette rupture dans le réseau, vous devez effectuer la coupe-min.
La coupe-min se fait après avoir trouvé un flot maximum avec Ford-Fulkerson.
Cette coupe va permettre de comprendre qu’elles seront les prochaines lignes qui seront en congestion.
Qu’en déduisez-vous ?
Rien ne vaut un exemple par un montage électronique représentant le réseau avec l’aide de LED pour montrer le flot et des résistances afin que le flot soit identique à vos calculs. Attention, vous avez de nombreux calculs à faire, notamment des ponts diviseurs de tensions !
Le fait de retirer un fil montrera l’impact sur le réseau (ceci est vrai au moment de la coupure, par la suite le réseau se réajuste).
Que remarquez-vous ?
Barème
- Dimensionnement de la ligne (7 points)
- Ecriture du graphe (3 points)
- Calcul du flot maximum (3 points)
- Conclusion (1 points)
- Coupure d’une ligne (7 points)
- Calcul du flot maximum (3 points)
- Trouver la coupe-min (3 points)
- Conclusion (1 points)
- Montage arduino (7 points)
- Calcul des résistances (5 points)
- Schéma Fritzing (1 points)
- Conclusion (1 points)
