Contenus
ToggleAlgorithme de Ford-Fulkerson
Afin d’initialiser l’algorithme, il est possible d’attribuer un flot quelconque dans le graphe en suivant des chemins simples (de la source vers le puits). Dans le schéma suivant, nous avons pris pour initialisation le chemin s-2-3-t.
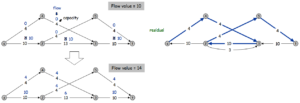
Il est possible de former une coupe à l’aide du dernier graphe d’écart. On applique un parcours à partir de s, tous les sommets pouvant être parcouru sont dans l’ensemble S, les autres dans l’ensemble T. En effet, les arcs saturés par le flots coupent le graphe en deux sous-ensembles, et forment la valeur de la coupe.
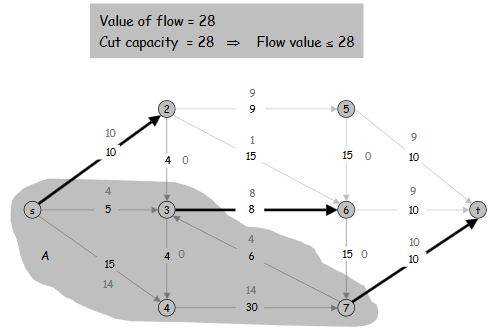
Si l’on souhaite augmenter le flot par un changement de valeur, il faudra augmenter le flot maximum pouvant passer par ces arcs.
L’algorithme de Ford-Fulkerson pas à pas
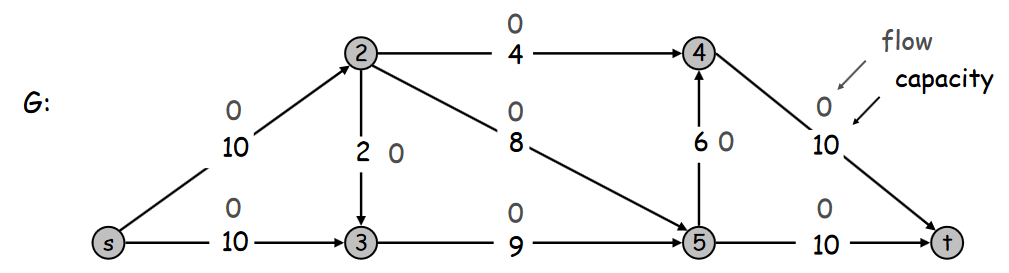
Le flot initial est de 0. Ici le graphe résiduel Gf est une copie du graphe G. Nous cherchons un chemin de s à t, par exemple s-2-5-t:

La valeur minimal du chemin est de 8.Nous rajoutons ce flot de 8 sur le chemin dans le graphe G.
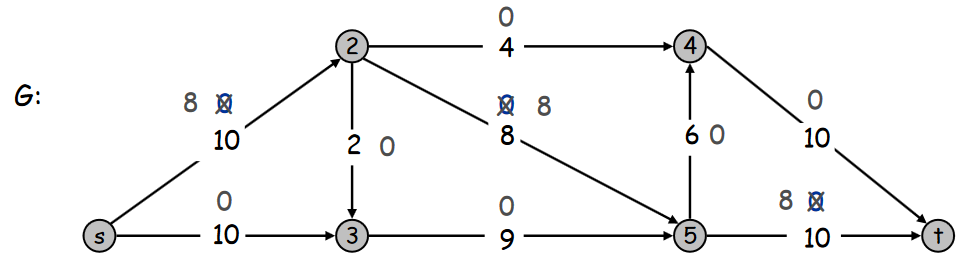
Pour rappel le graphe résiduel doit montrer les arcs inverses (représentant les flots). Le graphe résiduel de la nouvelle itération est le suivant :
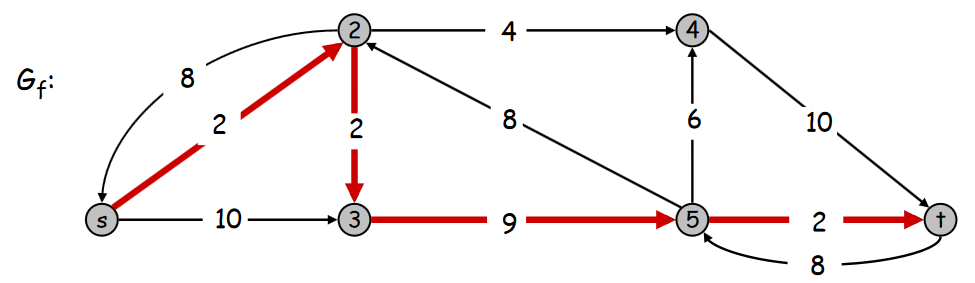
Ici nous choisissons le chemin s-2-3-5-t, avec 2 pour flot bloquant. Lorsque on choisit un arc inverse (donc représentant un flot) le nouveau flot dans le graphe G est réduit comme le montre ce nouveau graphe G.
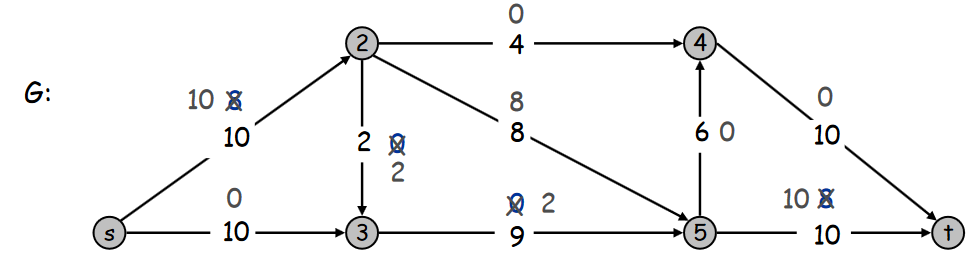
Valeur du flot = 10. Etc…
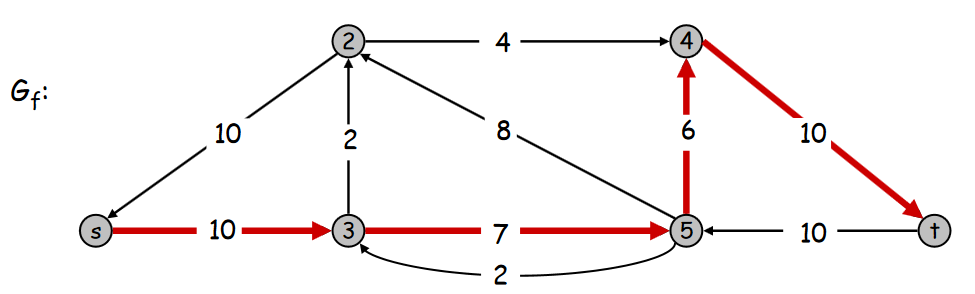
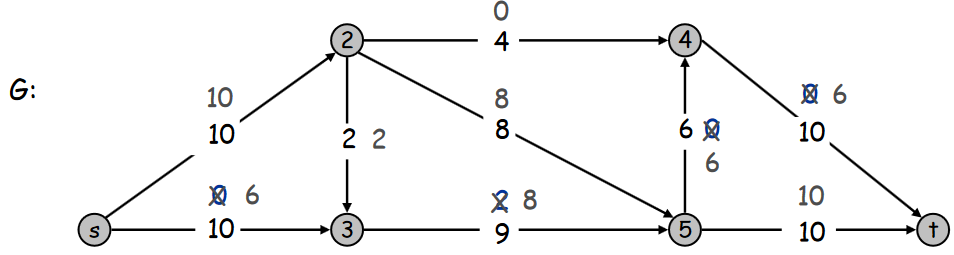
Valeur du flot = 16
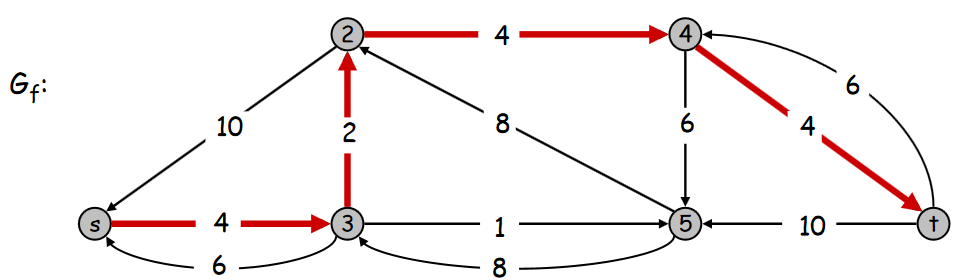
Choix de l’arc inverse (3,2) :
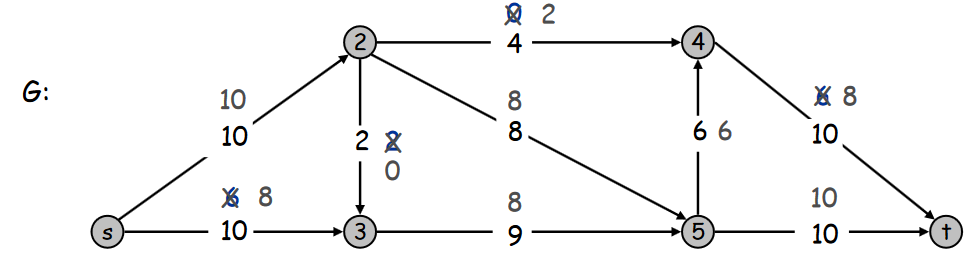
Valeur du flot = 18.
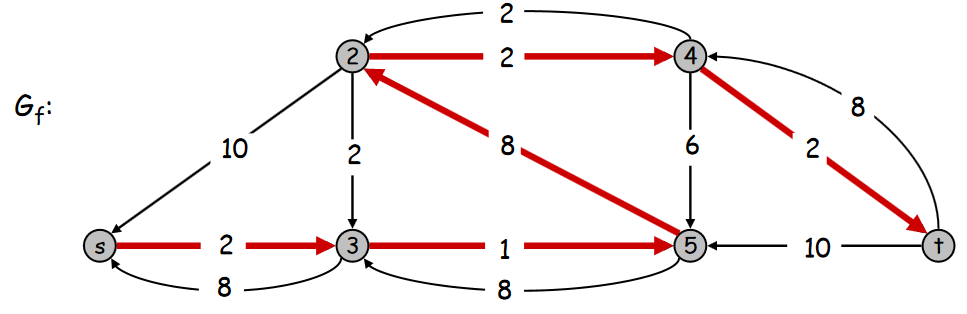

Valeur du flot = 19.
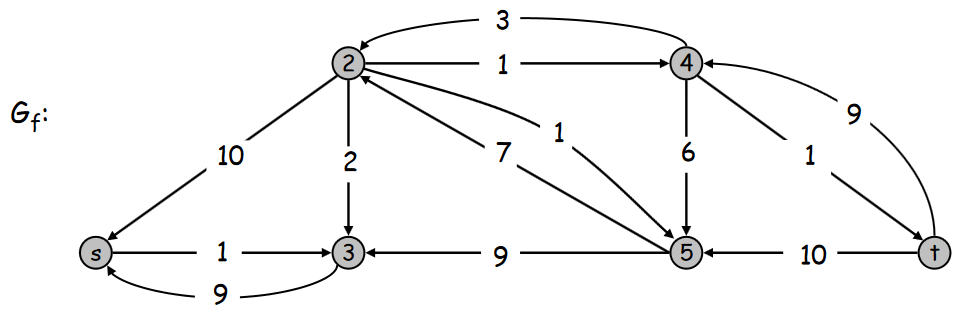
Il n’existe plus de chemin de s à t, nous avons trouvé un flot maximal pour ce graphe G.
