Contenus
ToggleAlgorithme d’Edmonds-Karp
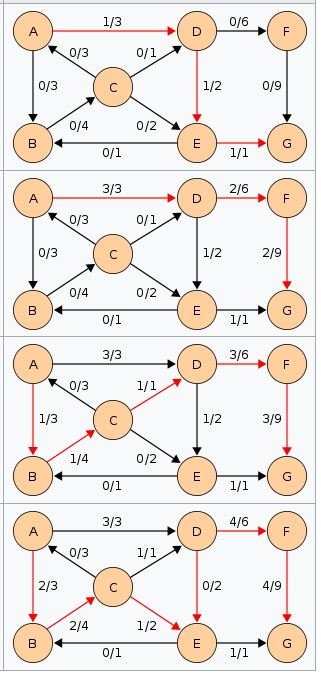
L’algorithme d’Edmonds-Karp à un temps d’exécution de O(VE²), il est plus rapide que l’algorithme de Ford-Fulkerson pour les graphes denses, c’est à dire un graphe contenant un grand nombre d’arête (ou arcs) en fonction du nombre de sommets.
L’algorithme d’Edmonds-Karp est identique à l’algorithme de Ford-Fulkerson, à l’exception de l’ordre de recherche utilisé pour déterminer un chemin augmentant. Le chemin trouvé doit être le chemin le plus court qui possède une capacité positive. Un tel chemin peut être trouvé par un parcours en largeur, en supposant que les arcs ont tous une longueur unité. On note que la longueur du chemin augmentant croît à chaque itération.
Code provenant de wikipédia
algorithm EdmondsKarp
input:
C[1..n, 1..n] (matrice des capacités)
E[1..n, 1..?] (listes des voisins)
s (source)
t (puits)
output:
f (valeur du flot maximum)
F (matrice donnant un flot valide de valeur maximum)
f := 0 (le flot initial est nul)
F := array(1..n, 1..n) (la capacité résiduelle de u à v est C[u,v] - F[u,v])
forever
m, P := BreadthFirstSearch(C, E, s, t, F)
if m = 0
break
f := f + m
(Backtrack et noter le flot)
v := t
while v ≠ s
u := P[v]
F[u,v] := F[u,v] + m
F[v,u] := F[v,u] - m
v := u
return (f, F)
algorithm BreadthFirstSearch
input:
C, E, s, t, F
output:
M[t] (capacité du chemin trouvé)
P (table des parents)
P := array(1..n)
for u in 1..n
P[u] := -1
P[s] := -2 (pour assurer que la source n'est pas redécouverte)
M := array(1..n) (capacité du chemin trouvé jusqu'au nœud)
M[s] := ∞
Q := queue()
Q.push(s)
while Q.size() > 0
u := Q.pop()
for v in E[u]
if C[u,v] - F[u,v] > 0 and P[v] = -1
P[v] := u
M[v] := min(M[u], C[u,v] - F[u,v])
if v ≠ t
Q.push(v)
else
return M[t], P
return 0, P