Teoría del lenguaje 101

Teoría del lenguaje

En teoría del lenguaje, el conjunto de entidades elementales se llama alfabeto. Una combinación de entidades elementales se llama palabra. Un conjunto de palabras se denomina idioma y se describe mediante una gramática. A partir de una gramática, podemos construir un procedimiento efectivo (llamado autómata) que permita decidir si una palabra es parte del lenguaje.

Hay diferentes clases de lenguajes, correspondientes a diferentes clases de gramáticas y autómatas. Entre los más sencillos de estudiar, la clase de lenguajes regulares corresponde a gramáticas regulares y autómatas finitos. Esta clase de gramática se usa generalmente para describir la automatización del hogar sin ciclos.

Una clase más global que los lenguajes regulares es la clase de lenguajes libres de contexto, correspondiente a gramáticas libres de contexto y autómatas pushdown. Esta clase de gramática, más poderosa que la clase de gramáticas regulares, se usa típicamente para la automatización del hogar con ciclos conocidos.

La teoría del lenguaje es útil para:

• describir el comportamiento automático (robótica, domótica, automatización de edificios)
• comprender todo un lenguaje y sus utilidades (compilador, ADN, aprendizaje automático)
• Minimizar un proceso automático (software integrado, tarjeta integrada para la industria aeroespacial o automotriz, etc.)

Alfabeto

Un alfabeto, indicado A, es un conjunto finito no vacío de símbolos (letras, signos, números, etc.)

Una palabra, definida en un alfabeto A, es una secuencia finita de símbolos / elementos de A.

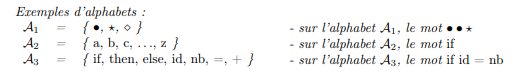
Algunas propiedades de las palabras:

• La longitud de una palabra u definida en un alfabeto A, denotada por | u | es el número de símbolos (su cardinal) que componen u.
• | u |_j cuenta el número de apariciones del símbolo j en la palabra u.
• La palabra vacía, anotada ε, se define en todos los alfabetos y es la palabra de longitud 0.
• El conjunto de todas las palabras formadas a partir del alfabeto A (resp. De todas las palabras no vacías) se denota con A^* (resp. A⁺).
• La concatenación de dos palabras uyv, denotadas uv o uv, es la palabra formada siguiendo los símbolos de u por los símbolos de v. Una n potencia de una palabra es esta palabra concatenada n veces.
• si uno o más símbolos están al poder + entonces significa que hay uno o más símbolos de este tipo en la palabra (ej. (ab)⁺= ab…)
• si uno o más símbolos están a la potencia * entonces significa que hay cero o más símbolos de este tipo en la palabra

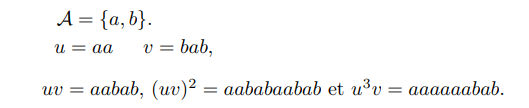
Dejemos que dos palabras uyv se definan en un alfabeto A.

u es un prefijo de v si y solo si existe una palabra w (potencialmente vacía) tal que uw = v.

u es un sufijo de v si y solo si existe una palabra w (potencialmente vacía) tal que wu = v.

u es un factor de v si y solo si hay dos palabras (potencialmente vacías) w₁ y W₂ como w₁uw₂= v.

una palabra no vacía u se dice que es primitiva si la ecuación u = v^I no admite una solución para i> 1.

dos palabras x = uv e y = vu deducidas entre sí por intercambio de prefijo y sufijo se dice que están conjugadas.

Idiomas

Un idioma, definido en un alfabeto A, es un conjunto de palabras definidas en A. Un idioma es un subconjunto de A^*.

Establecer operaciones definidas en idiomas: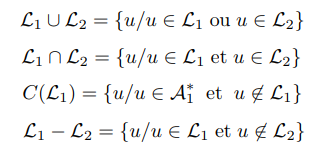

• La unión contiene todas las palabras que están contenidas en L₁ ya sea en L₂.
• Intersección es el lenguaje que contiene todas las palabras contenidas al mismo tiempo en L₁ y en L₂.
• El complemento de un idioma es el idioma que contiene todas las palabras que no están en ese idioma.
• La diferencia entre dos idiomas es el idioma que contiene todas las palabras de L₁ que no están en L₂.

Además de establecer operaciones sobre idiomas, el producto o concatenación de dos idiomas y definido por el idioma que contiene todas las palabras formadas a partir de la concatenación de una palabra de L₁ seguido de una palabra de L₂. El producto de las lenguas es asociativo pero no conmutativo.

El poder de una lengua es una concatenación sucesiva de esta lengua L^no= LL^n-1. El poder del 0 forma el lenguaje compuesto por la palabra vacía.

Considere, por ejemplo, los dos idiomas L₁ = {00, 11} y L₂ = {0, 1, 01} establecido en {0,1}. l₁.LOS₂ = {000, 001, 0001, 110, 111, 1101}.

Gramática

Un lenguaje puede describirse mediante un cierto número de reglas: la gramática indica cómo construir oraciones pertenecientes al lenguaje (operación en producción); la gramática también permite decidir si una oración determinada pertenece o no a la lengua (funcionamiento en reconocimiento).

Una gramática es un cuatrillizo G = (T, N, S, R) tal que:

• T es el vocabulario terminal, es decir, el alfabeto en el que se define la lengua.
• N es el vocabulario no terminal, es decir, el conjunto de símbolos que no aparecen en las palabras generadas, pero que se utilizan durante la generación. Un símbolo no terminal designa una categoría sintáctica.
• R es un conjunto de las llamadas reglas de reescritura o producción de la forma: u1 → u2, con u1 ∈ (N ∪ T)⁺ y u2 ∈ (N ∪)^*. Recuerde que + significa al menos un elemento y * significa 0 o más. El significado intuitivo de estas reglas es que la serie no vacía de símbolos terminales o no terminales u1 puede ser reemplazada posteriormente opcionalmente vacía de símbolos terminales o no terminales u2.
• S ∈ N es el símbolo o axioma inicial. Es a partir de este símbolo no terminal que comenzaremos la generación de palabras mediante las reglas de la gramática.

Cuando varias reglas gramaticales tienen la misma forma en la parte izquierda,
podrá factorizar estas diferentes reglas separando las partes rectas por líneas verticales. Por ejemplo, el conjunto de reglas S → ab, S → aSb, S → c podría escribirse S → ab | aSb | vs.

El lenguaje definido o generado por una gramática es el conjunto de palabras que se pueden obtener del símbolo inicial aplicando las reglas de la gramática. Más formalmente, introducimos las nociones de derivación entre formas, esta consiste en reemplazar un símbolo no terminal por una serie de símbolos terminales y no terminales según las reglas gramaticales.

Para obtener información adicional sobre las operaciones entre el lenguaje y la gramática, consulte la tabla de enlaces en la parte superior de este curso.