Language Theory 101

Language theory

In language theory, the set of elementary entities is called the alphabet. A combination of elementary entities is called a word. A set of words is called a language and is described by a grammar. From a grammar, we can build an effective procedure (called automaton) allowing to decide if a word is part of the language.

There are different classes of languages, corresponding to different classes of grammars and automata. Among the simplest to study, the class of regular languages corresponds to regular grammars and finite automata. This grammar class is typically used to describe cycleless home automation.

A more global class than regular languages is the class of context-free languages, corresponding to context-free grammars and pushdown automata. This class of grammar, more powerful than the class of regular grammars, is typically used for home automation with known cycles.

Language theory is useful for:

• describe automatic behavior (robotics, home automation, building automation)
• understand all of a language and its utilities (compiler, DNA, machine learning)
• Minimize an automatic process (integrated software, integrated card for the aerospace or automotive industry, etc.)

Alphabet

An alphabet, noted A, is a finite non-empty set of symbols (letters, signs, numbers, etc.)

A word, defined on an alphabet A, is a finite sequence of symbols / elements of A.

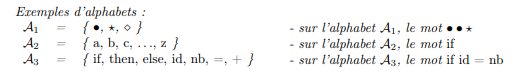
Some properties on words:

• The length of a word u defined on an alphabet A, denoted by | u | is the number of symbols (its cardinal) that make up u.
• | u |_j counts the number of occurrences of the symbol j in the word u.
• The empty word, noted ε, is defined on all alphabets and is the word of length 0.
• The set of all the words formed from the alphabet A (resp. Of all the nonempty words) is denoted by A^* (resp. A⁺).
• The concatenation of two words u and v, denoted uv or uv, is the word formed by following the symbols of u by the symbols of v. An n power of a word is this word concatenated n times.
• if one or more symbols is to the power + then it means that there is one or more symbol of this type in the word (ex. (ab)⁺= ab…)
• if one or more symbols is to the power * then it means that there is zero or more symbol of this type in the word

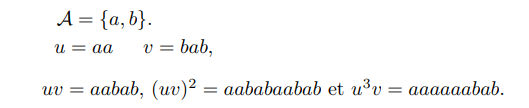
Let two words u and v be defined on an alphabet A.

u is a prefix of v if and only if there exists a (potentially empty) word w such that uw = v.

u is a suffix of v if and only if there exists a (potentially empty) word w such that wu = v.

u is a factor of v if and only if there are two (potentially empty) words w₁ and w₂ such as w₁uw₂= v.

a non-empty word u is said to be primitive if the equation u = vⁱ does not admit a solution for i> 1.

two words x = uv and y = vu deduced from each other by exchange of prefix and suffix are said to be conjugated.

Languages

A language, defined on an alphabet A, is a set of words defined on A. A language is a subset of A^*.

Set operations defined on languages: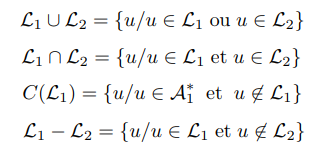

• The union contains all the words that are either contained in L₁ either in L₂.
• Intersection is the language which contains all the words contained at the same time in L₁ and in L₂.
• The complement of a language is the language containing all the words that are not in that language.
• The difference between two languages is the language containing all the words of L₁ which are not in L₂.

In addition to set operations on languages, the product or concatenation of two languages and defined by the language containing all the words formed from the concatenation of a word of L₁ followed by a word of L₂. The product of languages is associative but not commutative.

The power of a language is a successive concatenation of this language L^not= LL^n-1. The power of 0 forms the language composed of the empty word.

Consider for example the two languages L₁ = {00, 11} and L₂ = {0, 1, 01} set to {0,1}. L₁.THE₂ = {000, 001, 0001, 110, 111, 1101}.

Grammar

A language can be described by a certain number of rules: the grammar indicates how to construct sentences belonging to the language (operation in production); the grammar also makes it possible to decide whether or not a given sentence belongs to the language (functioning in recognition).

A grammar is a quadruplet G = (T, N, S, R) such that:

• T is the terminal vocabulary, that is to say the alphabet on which the language is defined.
• N is the non-terminal vocabulary, that is to say the set of symbols which do not appear in the generated words, but which are used during the generation. A non-terminal symbol designates a syntactic category.
• R is a set of so-called rewriting or production rules of the form: u1 → u2, with u1 ∈ (N ∪ T)⁺ and u2 ∈ (N ∪)^*. Recall that + means at least one element, and * means 0 or more. The intuitive meaning of these rules is that the non-empty series of terminal or non-terminal symbols u1 can subsequently be replaced optionally empty of terminal or non-terminal symbols u2.
• S ∈ N is the starting symbol or axiom. It is from this non-terminal symbol that we will start the generation of words by means of the rules of grammar.

When several grammar rules have the same form in the left part, we
can factorize these different rules by separating the straight parts by vertical lines. For example, the set of rules S → ab, S → aSb, S → c could be written S → ab | aSb | vs.

The language defined, or generated, by a grammar is the set of words which can be obtained from the starting symbol by applying the rules of grammar. More formally, we introduce the notions of derivation between forms, this consists in replacing a non-terminal symbol by a series of terminal and non-terminal symbols according to the grammar rules.

For additional information on operations between language and grammar, please refer to the links table at the top of this course.