Brzozowski and McCluskey algorithm

Difficulty

Hard 80%

Contents

Brzozowski and McCluskey's algorithm makes intensive use of the graphical representation of the automaton. The automaton itself is generalized, allowing, as transition labels, not only letters, but regular expressions. Starting from a automaton finished, we progressively eliminate the states, and at the end, we end up with an automaton having a single transition. The label of this transition is a regular expression for the language recognized by the automaton.

A generalized automaton is defined as a traditional non-deterministic finite automaton, with the following peculiarities:

it has only one initial state α and only one final state ω
transitions are labeled with regular expressions
no transition enters α and no transition leaves the final state ω.

We can easily transform an ordinary automaton TO into a generalized automaton: it suffices to add the states α and ω and ε-transitions from α to the initial states of TO, and ε-transitions of the terminal states of TO to ω.

Automaton reduction

Given a generalized automaton, we compute a generalized automaton having fewer transitions or states, by applying the transformations below without modifying the recognized language. At the end, there are only the two states α and ω and a transition of α and ω whose label is a regular expression denoting the recognized language. Transformations are reductions in transitions and reductions in states.

To reduce a state, all the paths passing through this state (to an adjacent state) must be performed. The language recognized by this path is then added to the reduced PLC (see the example).

The following example shows the main possible reductions as well as the regular expressions generated on the automaton:

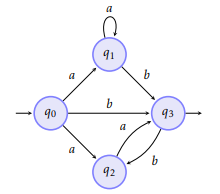
Which gives the following generalized automaton:

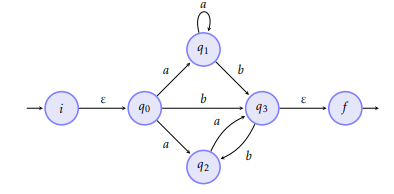
We eliminate q2: the path q0 -> q2 -> q3 gives the language a², it is therefore added to the path q0 -> q3. The path q3 -> q2 -> q3 gives the language ba or (ba) * because it is a loop on q3 -> q3

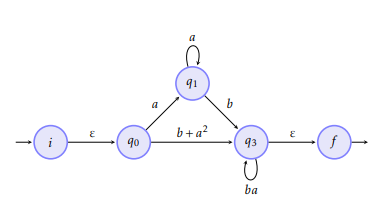
We eliminate q1: here the loop on q1 will give an a *

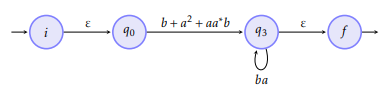
We eliminate q0:

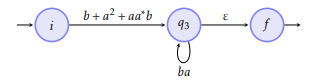
We eliminate q3:

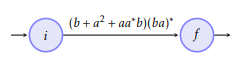
Note that the expression obtained also depends on the order of elimination, but that all the languages generated are equal.