Contents
Togglee-AFI to AFD
We now want to show that the language recognized by a automaton with empty transitions can also be done by a non-deterministic automaton without empty transitions (determination e-AFI towards AFD). This operation will require the addition of new transitions in the automaton.
Any language recognized by a AFN with ε–transitions can be recognized by an AFN (without ε–transitions) having the same number of states.
Construction of the AFN equivalent to an automaton with ε – transitions, by prolonging δ in δ1 (the transitive closure is all the states which can be reached by a state by a given transition).
First step: Addition of ε – transitions by transitive closure.
For all the states q accessible from p by ε-transition (in several steps), we add a direct ε – transition from p to q. We thus extend the function δ: δ1 (p, ε) = all the states accessible from p by ε – transition.
Second step: Addition of additional transitions and additional initial states, then removal of ε-transitions.
The initial states are all the states accessible from the initial states by ε – transition.
For any transition from p to q by a letter, we add transitions from p to r with the same letter for all ε – transitions from q to r: δ1 (p, a) = δ (p, a) ∪ (∪q∈δ (p, a) δ1 (q, ε)).
We remove all ε – transitions
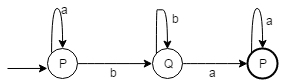
Example
The principle of the algorithm consists in replacing each path of length 1 starting with an epsilon-transition by a new transition which describes this path.

There are two paths of length 1 which start with the transition on epsilon:
- (1, ε, 3) (3, b, 3)
- (1, ε, 3) (3, c, 4)
We add to the automaton two new transitions which summarize these two paths:
- (1, b, 3)
- (1, c, 4)
And we remove the transition (1, ε, 3).
The algorithm is a little more complex in the cases where several epsilon-transitions follow one another and if they go into a final state, but the general principle presented here remains valid (it is enough to apply the first step).
The use of epsilon-transitions sometimes makes it possible to describe a language more clearly. It also makes it possible to simplify the description of certain operations (for example the union or the concatenation -> see automaton of Thompson).
The existence of epsilon-transitions makes the automaton non-deterministic since we always have the possibility of borrowing such a transition even when there is an ordinary transition that we could borrow.
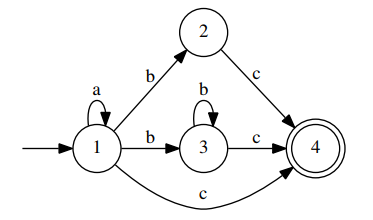
Another example
Consider the following automaton:

For this, it is first necessary to calculate, for each state, the ε-successors of each state p, that is to say the set of states q such that there exists a path formed only of ε-transitions starting from from p arriving in q.
We calculate the ε-successors of each state: Succε (p) = {q, r}, Succε (q) = {r}, Succε (r) = ∅.
We obtain the following NFA:
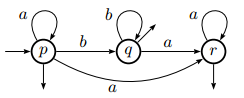
You can then determine it with the NFA to DFA method, or you can determine it directly in its form with espilon transition like the following example.
Let's take the automaton and transform it into a DFA:

The first step consists in calculating the epsilon-closing for each state of this automaton:
| Delta (Q) | To | b | Closure -> Q ' |
| p | p | – | {p, q, r} |
| q | – | q | {q, r} |
| r | r | – | {r} |
For each state of the closure, we calculate its transitions in the alphabet without epsilon:
| Delta (Q ') | To | b |
| {p, q, r} | {p, r} | {q} |
| {q, r} | {r} | {q} |
| {r} | {r} | – |
For each state obtained by the transitions, we calculate the closure:
| Delta (Q ') | To | b |
| {p, q, r} | {p, r} -> {p, q, r} | {q} -> {q, r} |
| {q, r} | {r} -> {r} | {q} -> {q, r} |
| {r} | {r} -> {r} | – |
Denote by {p, q, r} = P; {q, r} = Q and {r} = R. We obtain the following automaton: