This page offers corrected exercises on: battery-operated automaton.
Exercise 1
The (linear) grammar S → aSb | ε produces the language {anotbnot : n ≥ 0}. Based on this example, suggest grammars for each of the following languages: {a2n(bc)3n : n ≥ 0}, {a2nb3vs20n : n ≥ 0}, {a2nb3nvs20 : n ≥ 0}, {ambnot : m ≥ n ≥ 0}
1 - S → aaSbcbcbc | ε
2 - S → aaSc20 | bbb
3 - S → Xc20; X → aaXbbb | ε
4 - S → aS | aSb | ε
Exercise 2
Which language is generated by the following grammar:
S → aSa | aBa
B → bB | b
Give the battery-powered automaton generated by the following language: L (G) = {anotbmvsmd2n | n≥0, m> 0}.
In grammar, the first rule recursively generates as many a at each end of the word. The second rule generates at least one b inside the word. The generated language is therefore L (G) = {anotbmTonot | n> 0, m> 0}.
Before building the automaton, you must first of all understand the grammar rules. We notice that the extremities are in power n while the center in power m. The language can therefore be generated by rules of the type A → aAa | B. We deduce from this the two rules generating the language S → aSdd | TO ; A → bAc | bc
Exercise 3
We take an automaton producing in palindrome, that is to say words which can be read in the same way whether in left reading or in right reading. The automaton is then:
Give the transition table and all the derivations for the words ab and abb. Then show by a successful derivation that the words aaaa and baab are palindromes.
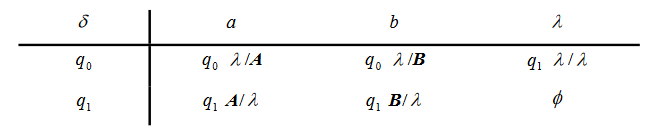
Derivation for the word ab:
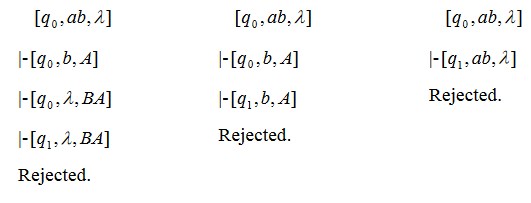
Derivation for the word abb:
Successful derivation for the words aaaa and baab:
Exercise 4
Let the alphabet be A = {a, b} and the language L = {a * b}. Write the grammar of this language. Find a battery-powered automaton that can read this language.
G = {T = {a, b}, N = {S}, S = {S}, P = {S -> b, S -> aS}}
Here we notice that the stack is not useful, the null use of a stack amounts to using an empty letter.
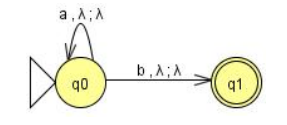
With lambda the empty letter.
Exercise 5
Let the alphabet A = {a, b} and the language L = {anot bp / n> = 0 and n <= p <= 2n}. Write the grammar of this language and show that it is an algebraic language. Find a battery-powered automaton that can read this language.
G = {T = {a, b}, N = {S}, S = S, P = {S -> ε | aSb | aSbb}}
We can also write the grammar in the following way
Note that the rules do respect the format of type 2 grammars. However, this grammar does not respect the type 3 format.
Z is the symbol that is placed in the stack at initialization (end of stack symbol).
Exercise 6
Write an algebraic grammar that can write any regular expression with the alphabet {0,1}. For information, the algebraic grammar contains the alphabet {0,1, (,), ∪, *, ∅, ε}. Testing on the regular expression (0 ∪ (10) * 1) *
Let's take the rules to form a regular expression:
0 or 1 only: S → 0 | 1
Empty word or epsilon: S → ∅ | ε
Union of two sub-words: S → S ∪ S
Concatenation of two sub-words: S → SS
Star of a sub-word: S → S *
Priority parentheses: S → (S)
By taking the word we obtain the following derivations:
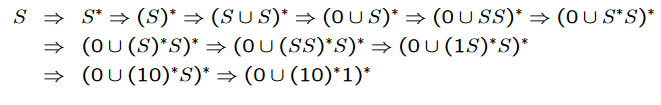
Which gives the following derivation tree:
EN 
FR 
ES