Contents
ToggleMinimization of AFD
Myhill-Nerode theorem (minimization of a AFD). Let L be a rational language. Among all L-recognizing AFDs, there is one and only one that has a minimal number of states.
Before minimizing an AFD, it must be completed, ie add a trash state like the state R on the diagram below.
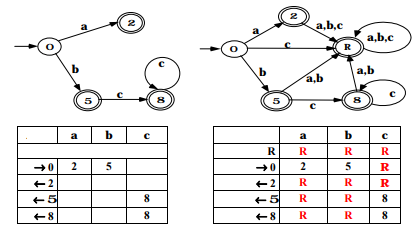
The minimization algorithm is as follows:
- Complete the AFD named D
- Construct an initial partition ∏ containing two sets I and II of states such that ∏ = {I = (terminal acceptance states of D), II = (other states of D)}
- For each state of D do
- Build the transition table
- Mark the states of departure and arrival according to their group of ∏
- If states of the same group of ∏ have divergent behaviors
- Separate the states into a new group (III for example) - preferably do only one separation per iteration.
- Return to 3
- End: the new states are the groups of ∏
Example
Let us take the example of AFD above. It is indeed deterministic as shown by the transition table.
Let's look at the transition table in step 3:
| To | b | vs | |
| 0 (I) | 2 (II) | 5 (II) | R (I) |
| 2 (II) | R (I) | R (I) | R (I) |
| 5 (II) | R (I) | R (I) | 8 (II) |
| 8 (II) | R (I) | R (I) | 8 (II) |
| R (I) | R (I) | R (I) | R (I) |
We notice when in group I, the behavior of O and R diverge, we will therefore separate them into two groups: I = (0) and III = (R)
Here is the new transition table:
| To | b | vs | |
| 0 (I) | 2 (II) | 5 (II) | R (III) |
| 2 (II) | R (III) | R (III) | R (III) |
| 5 (II) | R (III) | R (III) | 8 (II) |
| 8 (II) | R (III) | R (III) | 8 (II) |
| R (III) | R (III) | R (III) | R (III) |
We notice when in group II, the behavior of 2 and 5, 8 diverge, we will therefore separate them into two groups: II = (5, 8) and IV = (2)
Here is the new transition table:
| To | b | vs | |
| 0 (I) | 2 (IV) | 5 (II) | R (III) |
| 2 (IV) | R (III) | R (III) | R (III) |
| 5 (II) | R (III) | R (III) | 8 (II) |
| 8 (II) | R (III) | R (III) | 8 (II) |
| R (III) | R (III) | R (III) | R (III) |
We no longer observe any divergence between the groups, so we can perform the transition table with minimized AFD giving the following transition table:
| To | b | vs | |
| I | IV | II | III |
| IV | III | III | III |
| II | III | III | II |
| III | III | III | III |
The initial state is I (in relation to its equivalent in D), and the terminal states of the automaton are II and IV (in relation to their equivalents in D).
Another example
Consider the following automaton:

The initialization phase makes it possible to obtain the non-terminal group I and the terminal group II:
| TO | B | VS | D | |
| Init | I | II | I | II |
Let's look at the transitions for each state according to groups I and II:
| Alphabet | TO | B | VS | D |
| To | II | II | I | II |
| O | I | II | I | II |
Then we perform the separation of sets. Two states are in the same set if they were already in the same set and if the transitions lead in the same sets. In this example, B and D behave in exactly the same way, so they stay together. On the other hand, A and C which were part of the same set behave differently on the symbol "a". Consequently, the set noted I is divided into two. So we get:
| TO | B | VS | D | |
| Init | I | II | I | II |
| To | II | II | I | II |
| 0 | I | II | I | II |
| Separation 1 | I | II | III | II |
The current situation (the Balance sheet 1 line) is different than the starting situation. So we have to start over.
| TO | B | VS | D | |
| Init | I | II | I | II |
| To | II | II | I | II |
| 0 | I | II | I | II |
| Separation 1 | I | II | III | II |
| TO | II | II | III | II |
| 0 | III | II | III | II |
| Separation 2 | I | II | III | II |
The “Separation 2” line is identical to the “Separation 1” line. Consequently, in each of the remaining sets, the states are not distinguishable (they behave in exactly the same way and are therefore "redundant").
So we can build the new automaton by associating a state to each set. The transitions are indicated by the table. The initial state is the one containing the initial state of the starting automaton: here I contains state A, initial state. The final states are the states whose corresponding set contains at least one final state: here, II contains B and D which are final.
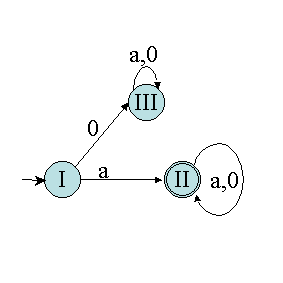
So far, we have "merged" the indistinguishable states. You must now delete all the remaining unnecessary states. In our example, state III is a sterile state (non-terminal and without transition), therefore useless. It must therefore be deleted. Hence the minimal deterministic automaton of the following figure:

