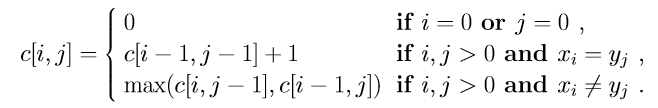Contents
ToggleCorrected exercises on dynamic programming
This page offers several corrected exercises for dynamic programming and divide and rule. The goal is to understand the difference between the Divide & Conquer paradigm and dynamic programming. The specifics of the path search (shortest path), problem of planning, maximum flow problem and more generally the graph theory is treated separately.

Exercise 1
Write pseudocode for a divide-and-conquer algorithm to find the position of the largest element in an array of numbers. Write a pseudocode for a brute force algorithm, compare with the previous one. Show a tree of the divide and conquer algorithm process. What is the maximum tree level for numbers?

The brute force algorithm is trivial: a loop.
At each level l, the complete binary tree is composed of 2^(l-1) leaves. So the total of the vertices is 2^l -1. Let l be the level of the tree, so l=sup(log_2 (n)).
Exercise 2
Suppose your input array is called A. What you need to do is form another array, say B, each i value of which is calculated using the recursive formula, max(A[i], B[i- 1]+A[i ])
What you actually do is choose to expand the previous window or start a new one. You can do this since you are only supposed to select continuous elements as part of your subsets.
5, -6, 7, 12, -3, 0, -11, -6
The answer would be 19 (from sub-array {7,12} )
Exercise 3
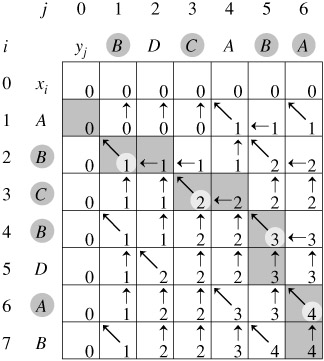
Use the longest common substring for: BDCABA and ABCBDAB. The algorithm is described as follows:

Exercise 4
Match the longest common substring to the longest common subsequence: BDCABA and ABCBDAB. The longest common subsequence (LCS) problem is to find the longest common subsequence of all sequences in a set of sequences (often only two sequences).
This differs from common substring search problems: unlike substrings, subsequences are not required to occupy consecutive positions in the original sequences.
Exercise 5
Levenshtein distance is a string metric for measuring the difference between two sequences. Informally, the Levenshtein distance between two words is the minimum number of single-character modifications (i.e., insertions, deletions, or substitutions) needed to change one word into the other. Propose a dynamic program to solve this problem. Trial with MEILENSTEIN and LEVENSHTEIN.
Exercise 6
Alice and Bob take turns playing a game, with Alice starting first.
Initially, there is a number n on the board. On each player's turn, that player makes a move consisting of:
Choose any x with 0 < x < n and n % x == 0.
Replace the number n on the board with n – x.
Also, if a player cannot move, they lose the game.
Return true if and only if Alice wins the game, assuming both players are playing optimally.
Example 1:
Input: n = 2
Output: true
Explanation: Alice chooses 1 and Bob has no more moves.
Example 2:
Input: n = 3
Output: false
Explanation: Alice chooses 1, Bob chooses 1 and Alice has no more moves.
To answer this problem, we will build a solution table. dp[i] indicates the result of the game for the given number i and for the player who started the game. Alice will try all the factors and choose the one that gives her opponent a losing value.

It is also possible to solve this problem in a more classic recursive way, called Top-Down.

And for a more practical side we are going to add a memosization.

Exercise 7
You are given a cost array of integers where cost[i] is the cost of the ith step of a stair. Once you've paid the cost, you can climb one or two steps.
You can either start from step with index 0 or from step with index 1.
Return the minimum cost to reach the top of the floor.
Example 1:
Entry: cost = [10,15,20]
Output: 15
Explanation: You will start at index 1.
– Pay 15 and climb two steps to reach the top.
The total cost is 15.
Example 2:
Input: cost = [1,100,1,1,1,100,1,1,100,1]
Output: 6
Explanation: You will start at index 0.
– Pay 1 and go up two steps to reach clue 2.
– Pay 1 and go up two steps to reach clue 4.
– Pay 1 and go up two steps to reach clue 6.
– Pay 1 and go up one step to reach clue 7.
– Pay 1 and go up two steps to reach clue 9.
– Pay 1 and climb a step to reach the top.
The total cost is 6.
For a first draft, we will solve this problem by recursive. For this we keep in mind the smallest cost by considering that we go back one step and two steps. And so on until you have the cost of the first or second step.
mincost(0) = cost[0]mincost(1) = cost[1]
mincost(i) = cost[i]+min(mincost(i-1), mincost(i-2))
Which gives the following code:

In a second step, we will stay in a top-down approach and add a memoization system. Thus, a minCost already found will not be recalculated later.

Finally, we will take the problem bottom-up to do dynamic programming;

Exercise 8
Alice and Bob are playing a game with piles of rocks. There are an even number of stacks arranged in a row, and each stack has a positive integer number of stone stacks[i].
The object of the game is to finish with the most stones. The total number of stones on all stacks is odd, so there is no tie.
Alice and Bob take turns, with Alice starting first. Each turn, a player takes the whole stack of stones either from the start or from the end of the row. This continues until there are no more stacks, at which point the person with the most stones wins.
Assuming Alice and Bob are playing optimally, return true if Alice wins the game, or false if Bob wins.
Input: stones = [5,3,4,5]
Output: true
Alice starts first and can only take the first 5 or the last 5.
Let's say she takes the first 5, so the line becomes [3, 4, 5].
If Bob takes 3, then the board is [4, 5], and Alice takes 5 to win with 10 points.
If Bob takes the last 5, then the board is [3, 4], and Alice takes 4 to win with 9 points.
This demonstrated that taking the top 5 was a winning move for Alice, so we return true.
Let's start with a top-down approach with memoization.
- Please note that both players play optimally, so we play optimally no matter who is Alice, who is Bob.
- Let dp(left, right) return [firstScore, secondScore] where firstScore is the maximum score when player1 plays first, secondScore is the maximum score when player2 plays second, he picks up stones in piles[left]…piles[ right ].
- For stones in piles[left]…piles[right], there are 2 choices for player1 to choose:
- Pick left: pickLeft = dp(left + 1, right).
- Player1's score = stacks[left] + pickLeft's second choice score, so firstScore = stacks[left] + pickLeft[1]
- Player2's score = pickLeft's first choice score, so secondScore = pickLeft[0]
- Pick right: pickRight = dp(left, right – 1).
- Player1's score = stacks[right] + pickRight's second score, so firstScore = stacks[right] + pickRight[1]
- Player2's score = pickRight's first choice score, so secondScore = pickRight[0].
- Pick left: pickLeft = dp(left + 1, right).
- We need to get the maximum score when player 1 plays first among more than 2 choices.
- Finally, dp(0, len(stacks) – 1) return [firstScore, secondScore], where alexScore = firstScore since Alice plays first, leeScore = secondScore since Bob plays second.

Now we are going to make a bottom-up algorithm while keeping memoization. Thus the algorithm will be in dynamic programming.

Exercise 9
There are soldiers standing in line. Each soldier is assigned a unique rank value.
You must form a team of 3 soldiers among them according to the following rules:
Choose 3 soldiers with index (i,j,k) with rating (rating[i],rating[j],rating[k]).
A team is valid if: (rating[i] < rating[j] < rating[k]) or (rating[i] > rating[j] > rating[k]) where (0 <= i < j < k < not).
Return the number of teams you can form given the conditions. (soldiers can be part of several teams).
Example 1:
Input: score = [2,5,3,4,1]
Output: 3
Explanation: Three teams can be formed depending on the conditions. (2,3,4), (5,4,1), (5,3,1).
Example 2:
Input: score = [2,1,3]
Output: 0
Explanation: We cannot form any team given the conditions.
It's easy to make a greedy algorithm. The latter is in O(n^3) so we will try to improve the complexity with dynamic programming.

Here is the main idea in the dynamic programming version:
First, we compute this case score[i] > score[j] > score[k] given that i > j > k. Next, compute the case score[i] < score[j] < score[k].
Set dp[i]: how many elements in the notation from 0 to i-1 are less than the notation[i].
For each time we found note[i] > note[j], we accumulate dp[j]. Here, dp[j] means how many notes[k] exist from 0 to j-1. That is, how many cases satisfy grade[i] > grade[j] > grade[k].

Exercise 10
You are given a price chart where price[i] is the price of a given stock on the ith day, and an integer fee representing transaction fees.
Find the maximum profit you can make. You can make as many transactions as you want, but you must pay transaction fees for each transaction.
Note: You cannot engage in multiple trades simultaneously (i.e. you must sell the stock before buying again).
Entry: price = [1,3,2,8,4,9], fee = 2
Output: 8
Explanation: Maximum profit can be achieved by:
– Buy at prices [0] = 1
– Sell at prices[3] = 8
– Buy at prices [4] = 4
– Sell at prices[5] = 9
The total profit is ((8 – 1) – 2) + ((9 – 4) – 2) = 8.
Let's start first with the top-down approach.
- Let dp(i, canBuy) be the maximum profit we can get from price[i..n-1] with canBuy flag == True means we can buy on the ith day.
- For the ith day we have 2 options:
- Ignore it: profit = dp(i+1)
- Buy it or sell it
- If buy: profit = dp(i+1) – price[i]
- If sale: profit = dp(i+1) + price[i] – commission

We will convert to a bottom-up approach to do more traditional dynamic programming.
Let dp[i][j] be the maximum profit we can make from price[i..n-1] with flag j == 1 means we can buy on the ith day.

Since our dp only accesses 2 states: the current dp state dp, the previous dp state dpPrev. We can optimize to O(1) in space complexity.

Exercise 11
You planned a train trip a year in advance. The days of the year on which you will travel are given as an integer number of days. Each day is an integer between 1 and 365.
Train tickets are sold in three different ways:
a 1 day pass is sold at the price of [0] dollars,
a 7-day pass is sold for costs [1] dollars, and
a 30-day pass is sold for costs [2] dollars.
Passes allow for as many consecutive travel days.
For example, if we get a 7 day pass on day 2, we can travel for 7 days: 2, 3, 4, 5, 6, 7 and 8.
Return the minimum number of dollars you need to travel each day in the given list of days.
Input: days = [1,4,6,7,8,20], costs = [2,7,15]
Exit: 11
For example, here is a way to buy passes that allow you to travel according to your travel plan:
On day 1, you purchased a 1-day pass for cost[0] = 2 $, which covered day 1.
On day 3, you bought a 7-day pass for cost[1] = 7 $, which covered days 3, 4, …, 9.
On day 20, you purchased a day pass for cost[0] = 2 $, which covered day 20.
In total, you have spent 11 $ and covered all the days of your trip.
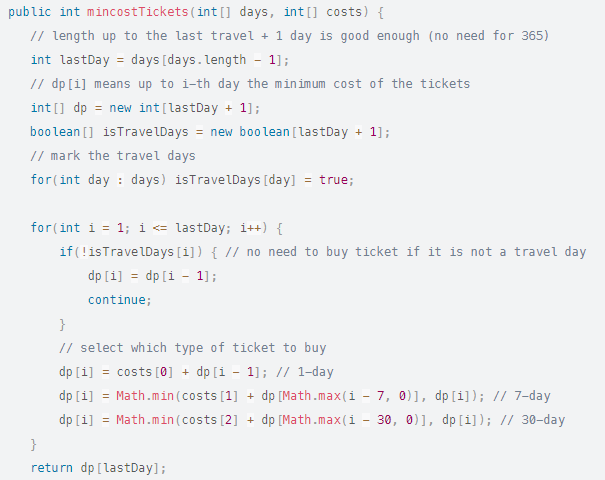
We will see here the bottom-up approach because the reasoning is very similar to the problem of backpack (knapsack) in building the solution.
dp[i] means until the th day the minimum cost of tickets. The size of the dp array depends on the last travel day, so we don't need an array length of 365.
We need a boolean array to mark the travel days, the reason is that if it's not a travel day, we don't need a ticket. However, if it is a travel day, we consider three scenarios (with three types of tickects):
If a 1-day ticket on day i, dp[i] = dp[i – 1] + cost[0]
If a 7-day ticket ends on day i, dp[i] = min(dp[i – 7], dp[i – 6] … dp[i – 1]) + cost[1]
If a 30-day ticket ends on day i, dp[i] = min(dp[i – 30], dp[i – 29] … dp[i – 1]) + cost[2]
But since the value of dp array increases, so:
For a 7-day ticket ending on day i, dp[i] = dp[i – 7] + cost[1]
For a 30-day ticket ending on day i, dp[i] = dp[i – 30] + cost[2]
Exercise 12
You are given an array of integer values where values[i] represents the value of the ith tourist site. Two tourist sites i and j have a distance j – i between them.
The score of a pair (i < j) of tourist sites is values[i] + values[j] + i – j: the sum of the values of the tourist sites, minus the distance between them.
Returns the maximum score of a pair of sights.
Input: values = [8,1,5,2,6]
Exit: 11
We have i = 0, j = 2, values[i] + values[j] + i – j = 8 + 5 + 0 – 2 = 11
Suppose we choose the site [i,…j]. The score can be broken down into 2 parts.
The first part is the startGain that you earn by starting at a certain point i. Note that startGain[i] = a[i] + i.
The second part is the endGain which is the amount you earn by finishing at a certain point j. Note that endGain[i] = a[j] – j.
Note that endGain can be negative.
The overall gain for [i,…j] is nothing but startGain[i] + endGain[j]. (This can be easily verified by the definitions).
We must maximize the overall gain.
What are the possible positions to start the journey? It is clear that we can start everything except the last element. Thus, the optimal journey must begin at one of these elements.
Suppose we are only allowed to start a journey at i. What is the maximum amount we can win in this case? Well, since the startGain is fixed, we need to maximize the endGain. We can do this by stopping at an element that has the maximum endGain provided it appears to the right of i.
As shown above, for each i we need to find the maximum endGain to its right.
maxEndRight[i] = max(maxEndRight[i+1], endGain[i+1]) = max(maxEndRight[i+1], a[i+1] – (i+1))
maxEndRight[i] represents the highest endGain you can get by stopping at any point strictly to the right of i. Since by definition we already know endGain[i+1] (the highest possible gain when ending at any point to the right of i+1), we only have to check the possibility of knowing if s stopping at i+1 would be beneficial or not. Hence the definition of DP.
For each valid i, overallGain[i] = startGain[i] + maxEndRight[i] = a[i] + i + maxEndRight[i]
Note that maxEndRight[i] only depends on maxEndRight[i+1]. Therefore, we can use 2 variables to track previous values.
Since we need the value of maxEndRight[i+1] to calculate the value of maxEndRight[i], so we start the iterations from the back.
As stated, trips cannot start at the last element, so the for loop starts at i=n-2. For this value, maxEndingRight is initialized to endGain[lastIndex] because that is the only possible way to end the trip.

Exercise 13
You are a professional thief planning to rob houses along a street. Each house has a certain amount of money hidden away, the only constraint preventing you from robbing each of them is that the adjacent houses have security systems connected and it will automatically contact the police if two adjacent houses were robbed on the same night.
Given an array of integer nums representing the amount of money in each house, return the maximum amount of money you can steal tonight without alerting the police.
Input: numbers = [1,2,3,1]
Output: 4
Explanation: Steal house 1 (money = 1) then steal house 3 (money = 3).
Total amount you can steal = 1 + 3 = 4.
Input: numbers = [2,7,9,3,1]
Output: 12
Explanation: Steal house 1 (money = 2), steal house 3 (money = 9) and steal house 5 (money = 1).
Total amount you can steal = 2 + 9 + 1 = 12.
Let's find a recursive relation.
A thief has 2 options: a) steal the current house i; b) do not rob the current house.
If an 'a' option is selected, that means she can't steal the previous i-1 house, but can safely switch to the one before the previous i-2 and get all cumulative loot that follows.
If a “b” option is selected, the thief gets all possible loot from the theft of i-1 and all subsequent buildings.
It therefore comes down to calculating what is the most profitable:
theft from the current house + loot from the houses before the previous one the loot from the previous house theft and any loot captured before that
rob(i) = Math.max( rob(i – 2) + currentHouseValue, rob(i – 1) )
This would give the following recursive version:

Now let's think about a method using memoization. For this, we are going to consider that when adding each house (thus at stage i, either we do not steal this house (thus same value as stage i-1), or we steal the house and therefore potentially that in i-2.
We therefore take the maximum between the optimum in stage i-1 and in i-2 + value of the new house. As a reminder, each step is optimal because solving the problem with without the new house is optimal by principle of sub-problem.
Which give :

We are here on a complexity in memory and in time in O(n).
Let's transform this code is bottom-up, so in dynamic programming:
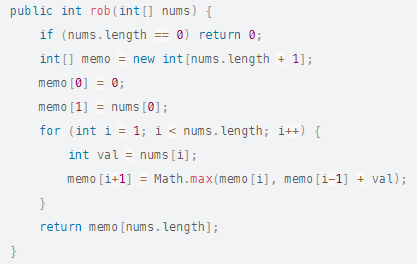
Note that like Fibonacci we do not need to keep the set of previous values because the optimal subproblem in i-1 and i-2 does not change whatever the new house. Note that this optimization will not allow you to know which houses have been chosen!

The space complexity is O(1).
Exercise 14
You are given k identical eggs and you have access to a building of n floors numbered from 1 to n.
You know that there is a floor f where 0 <= f <= n such that any egg dropped on a floor higher than f will break, and any egg dropped at or below floor f will not break.
With each move, you can pick up an unbroken egg and drop it from any floor x (where 1 <= x <= n). If the egg breaks, you can no longer use it. However, if the egg doesn't break, you can reuse it in future moves.
Returns the minimum number of moves you need to determine with certainty what the value of f is.
Input: k = 1, n = 2
Output: 2
Drop the egg from tier 1. If it breaks, we know that f = 0.
Otherwise, drop the egg from tier 2. If it breaks, we know that f = 1.
If it doesn't break, then we know f = 2.
Therefore, we need at least 2 moves to determine with certainty what the value of f is.
First, we can see that to get the response of larger floors and eggs, the results of smaller cases are useful for analysis, which leads to dynamic programming.
Then, how to define a state for each drop in order to obtain the optimal floor? Here we have two variables:
The number of eggs left to discard i, (0 <= i <= K)
The number of floors left to test j, (1 <= j <= N)
The answer (the smallest times to obtain the optimal floor) can be the value of each state dp.
The base case is rather intuitive to find. Consider the cases with smaller eggs and floors:
dp[1][j] = j, j = 1…N # an egg, check each floor from 1 to j
dp[i][0] = 0, i = 1…K # no floor, no drop necessary to obtain the optimal floor
dp[i][1] = 1, i = 1…K # one stage, check only once
To obtain a recursive relation, consider a test case: 3 eggs and 100 floors.
For the next drop, I can choose a stage from 1 to 100, let's say I choose 25.
There are 2 possible outcomes for this drop:
the egg broke, I now have 2 eggs, and the floor to choose from becomes 1~24.
the egg remains safe, I still have 3 eggs, and the floor to choose from becomes 26~100.
Thinking of the worst case scenario and using the dp definition above, we can describe the situation of getting the optimal floor by choosing floor 25 for the next drop as:
dp[3][100] = 1 + max(dp[2][24], dp[3][75])
Besides floor 25, in term of next dropped, we can also choose floor from 1 to 100.
Each drop would be similar to the case of 25 above. The end result would be the minimum of all possible choices of the following floors to drop:
dp[3][100] = min(…, 1 + max(dp[2][23], dp[3][76]), 1 + max(dp[2][24], dp[3][ 75]), 1 + max(dp[2][25], dp[3][74]), …) (take floor 24, 25, 26 as an example)
To generalize the example above, the formula dp would be:
dp[i][j] = min(1 + max(dp[i-1][k-1], dp[i][jk])), k = 1.2,…j
Therefore, we define dp[i][j] as the smallest number of drops to obtain the optimal floor with i eggs and j floors remaining.
Here is a first brute force solution in O(kn^2)

However, this idea is very brute force, because you check all the possibilities.
So I look at this problem in a different way:
dp[M][K] means that, given K eggs and M moves, what is the maximum number of floors we can check.
The dp equation is: dp[m][k] = dp[m – 1][k – 1] + dp[m – 1][k] + 1,
which means we take 1 move to a floor, if the egg breaks then we can check dp[m – 1][k – 1] floors. if the egg does not break, then we can check dp[m – 1][k] stages.
Which would give the following code:

Do not try this code, you will have a TLE! It should be optimized with a Binary Tree that we will do in another course!
Exercise 15
The demons captured the princess and imprisoned her in the lower right corner of a dungeon. The dungeon consists of mxn rooms arranged in a 2D grid. Our valiant knight is initially positioned in the upper left room and must fight his way through the dungeon to save the princess.
The knight has an initial number of life points represented by a positive integer. If at any time his hit points drop to 0 or below, he dies immediately.
Some rooms are guarded by demons (represented by negative integers), so the knight loses health when entering these rooms; other rooms are either empty (represented by 0) or contain magic orbs that increase the knight's health (represented by positive integers).
To reach the princess as quickly as possible, the knight decides to move only to the right or down with each step.
Give the knight minimum initial health so he can save the princess.
Note that any room can contain threats or power-ups, even the first room the knight enters and the lower right room where the princess is imprisoned.
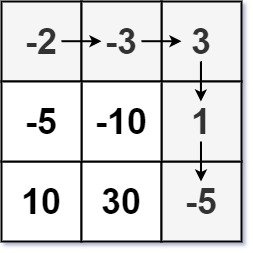
Entrance: dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
Output: 7
Explanation: The knight's initial health must be at least 7 if he follows the optimal path: RIGHT -> RIGHT -> DOWN -> DOWN.
Probably when you see this problem and you have some experience in such type of problems, you can guess that it is a dynamic programming problem. However, even if you understand this, it is not easy to solve it. Let's use dp from top to bottom, i.e. Let dp[i][j] be the minimum hp we need to reach the princess if we start from point (i,j). Consider the following example:
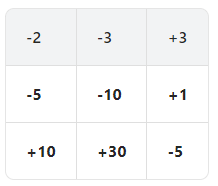
Let's add a dummy row at the bottom and a dummy column at the right to more easily handle border cases. We fill it with infinity, except two – neighbors of our princess. I'll explain that a bit later.
How to evaluate dp[i][j]? We need to examine two cells: dp[i+1][j] and dp[i][j+1] and evaluate two possible candidates: dp[i+1][j]-dungeon[i][j] and dp [i][j+1]-dungeon[i][j].
- If at least one of these two numbers is negative, it means that one can survive with just 1 hp: (look at the number +30 in our table for example)
- If these two numbers are positive, we must take the minimum, see for example the number -10 in our table: to survive we need either 5- -10 = 15 if we go to the right and 1- -10 = 11 if we goes down, of course we choose 11.
These conditions can be written on an equation: dp[i][j] = max(min(dp[i+1][j],dp[i][j+1])-dungeon[i][j], 1).
Finally, why did I put 1 to 2 princess neighbors? To make this formula valid for the princess cell: if we have a negative number like -5 in this cell, we need 6 gp to survive, if we have a non-negative number in this cell, we need 1 gp to survive.
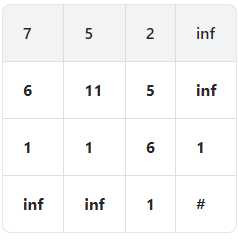
The space and time complexity is O(nm)

It's also possible to do it with dp descending, but in that case you have to use binary search, because you don't know in advance whether you're surviving from x HP or not. The complexity will be O(nm log(MAX_HP)) in this case.
Exercise 16
You are given a rows x cols matrix grid representing a field of cherries where grid[i][j] represents the number of cherries you can collect from cell (i,j).
You have two robots that can pick cherries for you:
The #1 robot is located in the upper left corner (0, 0) and
The #2 robot is located in the upper right corner (0, cols – 1).
Return the maximum number of cherry pick-ups using both bots by following the rules below:
From a cell (i, j), robots can move to the cell (i + 1, j – 1), (i + 1, j) or (i + 1, j + 1).
When a robot passes through a cell, it collects all the cherries and the cell becomes an empty cell.
When the two robots stay in the same cell, only one takes the cherries.
The two robots cannot leave the grid at any time.
Both robots must reach the bottom row of the grid.

Input: grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0, 0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
Output: 28
Explanation: The trajectories of robots 1 and 2 are described in green and blue respectively.
Cherries taken by Robot #1, (1+9+5+2)=17.
Cherries taken by Robot #2, (1+3+4+3)=11.
Total cherries: 17 + 11 = 28.
In this problem, we will assume that both robots will move to the next row at the same time so that they both stay in the same row. This will be the first preview to solve this problem.
As described in the problem statement, we can move in 3 directions (i+1, j-1) , (i+1, j) or (i+1, j+1). All in the next row but with a different column.
Since we have 3 directions for each robot, there are therefore in each row 9 (3 x 3) states that we can move towards. (3 states for the first robot and 3 states for the second robot so it's 3 x 3).
And as the hint says, we need to have a 4 row DP array. Since this is a 3-dimensional array, there will be a 2-dimensional array which will be n*n, i.e. no. of column * no. of column. Where the row will be defined by the position of the Robot1 column and the column will specify the position of the Robot2 column.
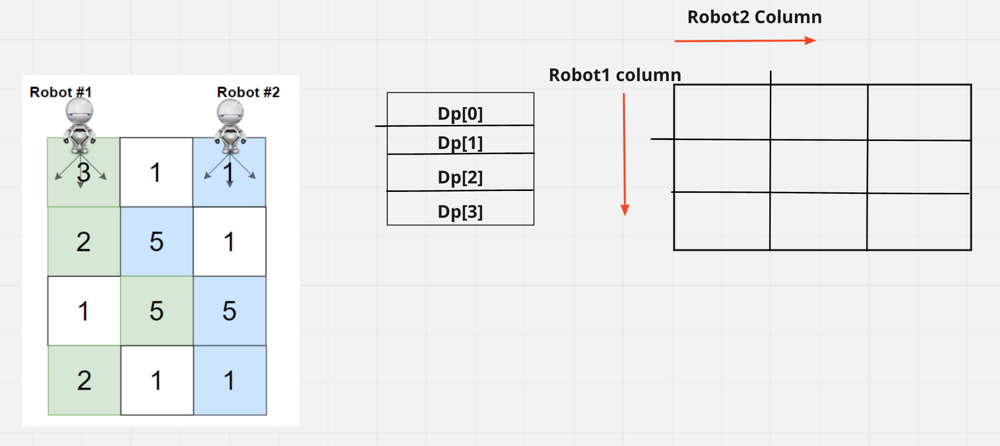
Initially, we know that robot1 is at position 0 and robot2 is at position column – 1, which is the last column.
We have to fill dp[0] i.e. 1st row and in this 1st row column position for robot will be (0, 2) because 0 means column position for robot1 and 2 means position column for robot2 in the grid.
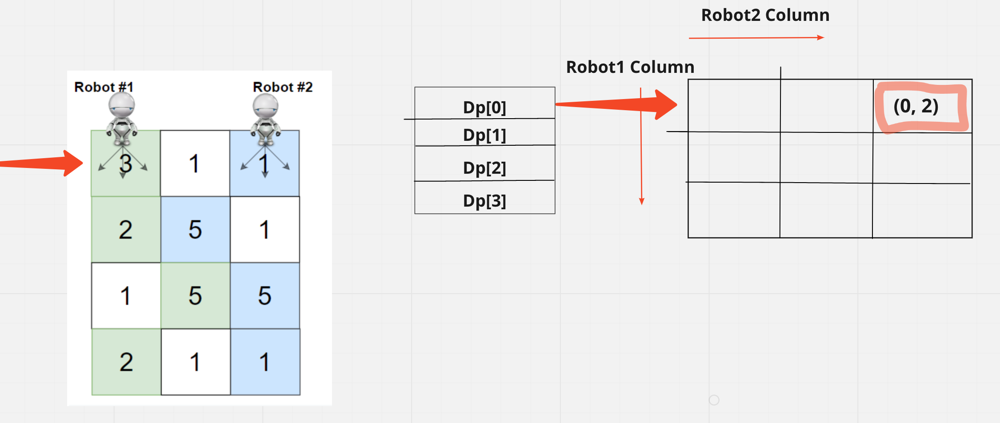
When we fill the space we get the value 3 + 1 which is 4
Now we need to fill the 2nd row. And in the 2nd line also there will be an n*m matrix. If we take robot1's previous position as 0, we have 3 columns it can go into in the next row, i.e. col {-1, 0, 1}. As col1 is out of range, we discard this "-1" and keep only "0, 1"
And the same robot2 is in 2, we can either reach the col {1, 2, 3}. Since col3 is out of bounds, we discard "3" and keep only "1, 2"
Now when we create the combination of all the columns that robot1 and robot2 can be we get 4 values and when we fill it it will be:
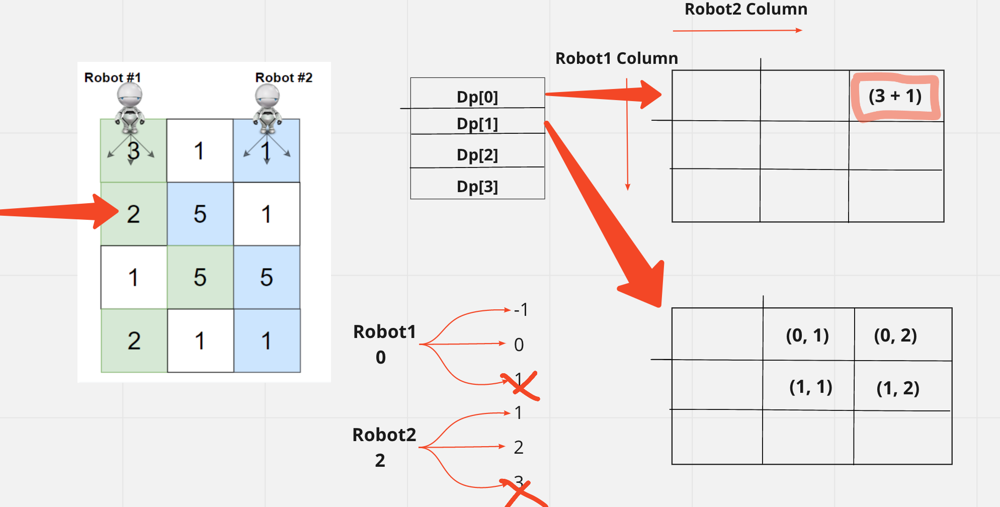
So if we look for (0, 1) the value that returns will be grid[0][1] + grid[1][1] + prev. But for (1,1) it will be grid[1][1] + prev.
If we now talk about code. Let's take dp[row][column][column] our dynamic programming. At the beginning col1=0 and col2=column-1 (robot location).
We have the solution max=dp[0][col1][col2].
Here is the code to fill for each increasing value of dp[raw][][]
// now comes apart where we need to iterate over each row;
for(int i = 1; i < row; i++){ // each row starting with 1
// In this each row of dp, we need to excise our logic picking that particular column, as the starting position
// we need to loop on all the columns precise in this row
// as i told there will be n*m column
for(int c1 = 0; c1 < collar; c1++){
for(int c2 = 0; c2 < collar; c2++){
// now from every column we need to fill the cube; for all the combinations or all the cell we can reach; with respective robot1 & robot2
// now we need to 1st take the previous value, that we discussed
int prev = dp[i - 1][c1][c2];
yew(prev >= 0){ // if that the case, we need to perform our operation, if it is a -ve value it means that we haven't reach yet that particular cell. And above that's why we initialize the whole array with -1
// Now we need to iterate over all the combinations of column that c1 & c2 can be in. For that we had define a direction array at the top
for(int d1: direction){ // for c1 we have the direction "d1" and we iterate over it
col1 = d1 + c1; // and column1 will be d1 + c1
for(int d2: direction){ // for c2 we have the direction "d2" and we iterate over it
col2 = d2 + c2; // and column2 will be d2 + c2
// Now we need to check is the new col1 & col2 are in the range of 0 & col. And for that we need to create a new method, which will check is the new col1 & col2 are in the range
yew(inRange(col1, collar) && inRange(col2, collar)){
dp[i][col1][col2] = Math.max(dp[i][col1][col2], prev+(col1 == col2 ? grid[i][col1] : (grid[i][col1] + grid[i][col2]))); // if the value are int this range, we need to update the col1 & col2 position in the i'th row
max = Math.max(max, dp[i][col1][col2]); // we need to update the maximum at each step. Taking max of max value & also the new column that we have filled
}
}
}
}
}
}
}
return max; //eturn max at the endLet's call dp' the upward approach. Here's better optimized code using a top-down approach to the original problem.
dp[k][i][j] indicates if the two robots start from grid[k][i] and grid[k][j] the maximum total number of cherries they can finally pick up. Note that they can only move down.
After filling dp, the final answer is dp[0][0][COL_NUM – 1]
For the last grid line, we have dp[-1][i][j] = grid[-1][i] if i == j else grid[-1][i] + grid[-1][ j]. Note that if 2 robots stay in the same place, they can only pick up once.
For the other rows, we have to iterate over all the 3*3 direction combinations they can choose from in the next layer and find the maximum, because for each robot there are 3 directions they can move.
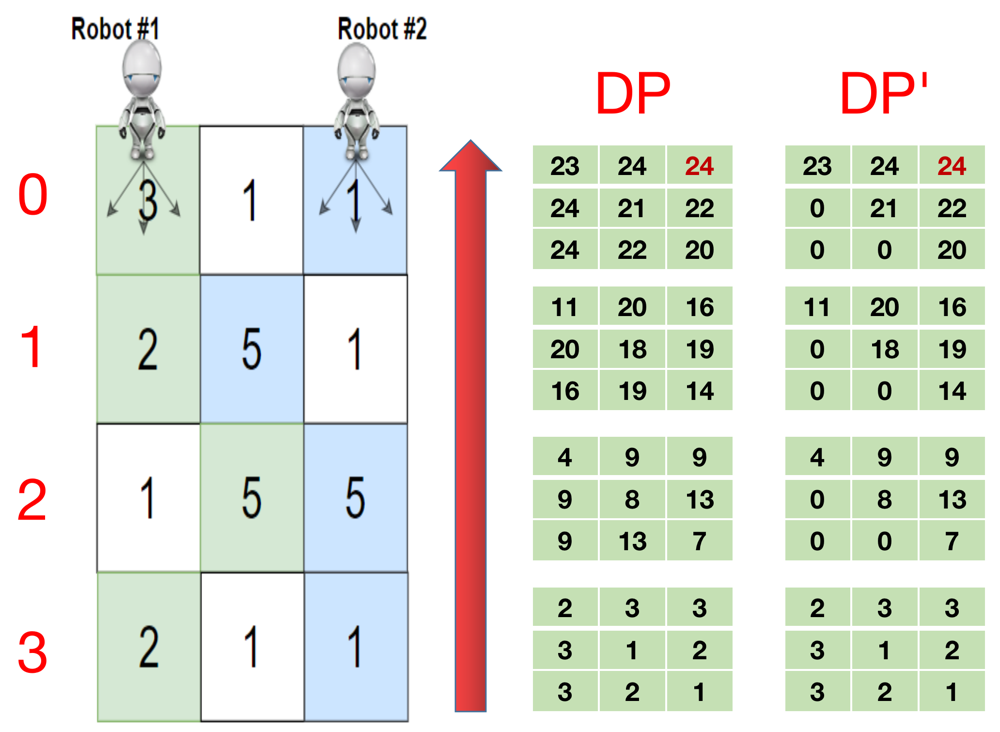
We will therefore have the following code:

It's not very optimal. Here is a better optimized code in python (in 2D with a DFS approach):