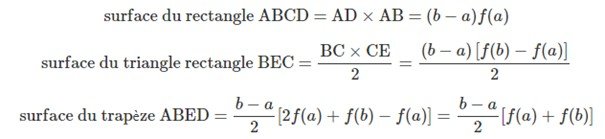Contents
ToggleCorrected exercises with divide and conquer algorithm
The following corrected exercises concern the creation of algorithms according to the structure of the divide and rule (divide&conquer). Algorithms of the dichotomy type will also be studied.

Exercise 1
We are going to play the game of “smaller, bigger”. The goal is to guess a number between 1 and n (integer). We consider that the algorithm takes as input the value of n and the number x to guess, and that it returns the number of moves to find this number.
a – State the problem more formally.
b – Write the iterative algorithm solving this problem.
c – Write the algorithm recursive solving this problem.
d – Compare complexities.
a – The problem could be rewritten as follows: Given an array sorted in ascending order of integers, how to determine whether an element belongs to this array or not? The principle is well known: the element sought is compared to the median element, and if necessary, the search is repeated in the left or right part of the table.
b- The iterative algorithm is as follows:

Since the array is cut in two each time, we will go through at most log n element before finding the right one or knowing that it does not exist. The complexity is therefore O(log n)
vs - By default the response of the algorithm is false, unless there is a true which is returned which will give in the main then the method:

Since the operation is exactly the same as the iterative algorithm, one suspects that the complexity is the same.
Exercise 2
We are looking for the sum of an array B of n integer elements.
1 – Write a divide-and-conquer algorithm that solves this problem.
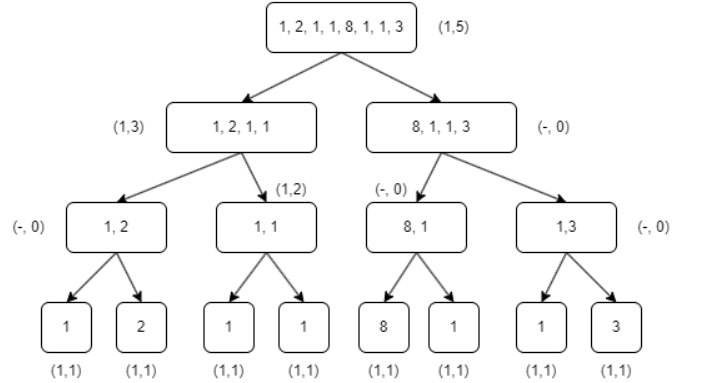
2 – Analyze its complexity and make the call tree for the array [3,4,2,3,4].
3 – Compare it with an iterative algorithm that you will describe
We define the function Sum(B,i,j) which is the sum of the elements of B between positions i and j. So the sought value is Sum(B,1,n). We will calculate Sum(B,i,j) by dividing the array B[i..j] into two halves; calculating sums for each half; and adding these two sums. This gives the following code:

For complexity, since we haven't seen the Master Theorem yet, we'll use the call tree:

We understand that we cut the painting in two each time. The calculation is simple, so the complexity only depends on the depth of the tree p such that 2^p > n (array size) hence p > log n and a complexity of O(log n).
The iterative algorithm is as follows:

Here the complexity is O(n).
Exercise 3
We say that an array has a majority element if a value of the array is present at least n/2 times out of n elements.
1 – Propose an iterative algorithm to solve this problem.
2 – Propose a method to solve this divide and conquer problem.
3 – Write the method described by an algorithm.
Modify your algorithm taking into account the following properties:
- if only one of the halves provides a majority, only that element can be a majority in the full array.
- if the two recursive calls provide majorities, they are different, with a different number of occurrences: the only one that can be a majority is the one with the greatest number of occurrences.
- in the case where n is a power of 2, and therefore the halves always of equal size, if there are two different majorities with the same number of occurrences, then there can be no majorities in the complete table.
1 – We count the number of occurrences of each element (no need to count to the left because if it exists then it has already been counted before). For the first loop, we could have stopped at n/2 + 1 because even if all the following elements were identical, it would still not be the majority.

2 – We will start from the principle of divide and conquer:

If there is a majority element x in E, then x is in the majority in at least one of the two lists E1 and E2 (indeed if x does not have a majority in E1, nor in E2, then in E, number of x ≤ n/4 + n/4 = n/2).
The principle of recursion is then as follows: calculate the majority elements of E1 and E2 (if they exist) with the total number of occurrences of each and deduce whether one of the two is the majority in E.
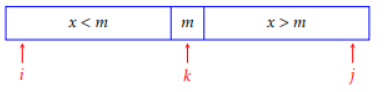
The following algorithm Majority(i, j) returns a couple which equals (x, cx) if x is the majority in the sub-array E[i..j] with cx occurrences and which equals (−, 0) if it there is no majority in E[i..j], the initial call being Majority(1, n). The Occurence(x, i, j) function calculates the number of occurrences of x in the sub-array E[i..j].

It is not so easy to understand, let's take an example of an 8 element array with 5 identical elements to fully understand how it works.
Here is the majority algorithm taking into account the new properties:

Exercise 4
1 – Propose a divide-and-conquer algorithm seeking the minimum of an array.
2 – Likewise with the maximum.
3 – Similarly by looking for both the minimum and the maximum.
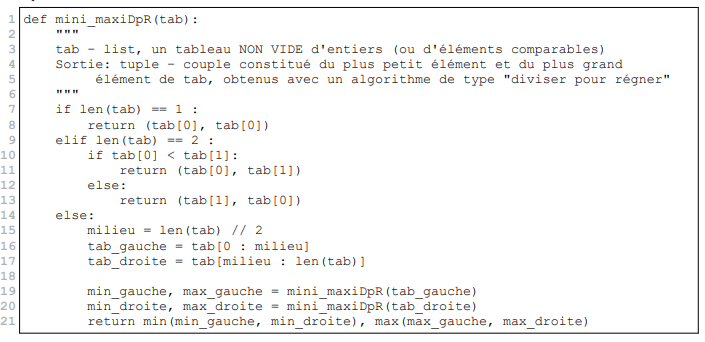
I will give the answer directly to question 3 since it contains the answer to the two previous ones. In this method, it is necessary to remember the positions in the table as well as the value of min and max.
Exercise 5
Here is the matrix product formula:
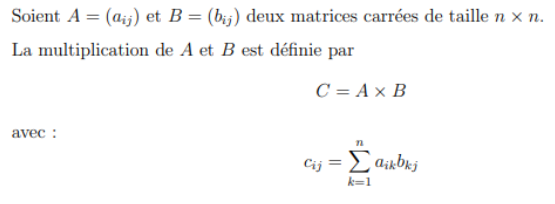
1 – Propose an iterative algorithm and give its complexity.
To decompose a matrix into a dichotomy, it must be done both on the rows and on the columns, therefore in 4 parts like the following diagram:
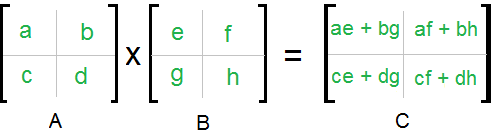
Each element is a square matrix. Let us denote r=ae+bg, s=af+bh, t=ce+dg and u=cf+dh.
2 – Strassen has found a method to further reduce the number of calculations. It proposes to calculate r, s, t, u using a linear combination (addition or subtraction) of the following matrices:

Express r, s, t, u in terms of pi.
3 – Propose a recursive algorithm based on Strassen's calculations for the matrix product.
1 – We notice in the formula that we will have to make three loops according to i, j and k.

Deep within the iteration structures, there are three nested 1 to n loops, so a complexity of O(n^3)
2 – This gives the following linear relations:
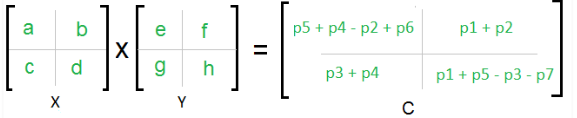
3 – The divide and conquer algorithm is as follows:

Exercise 6
Write a pseudo code for a Divide and Conquer algorithm to find the position of the largest element in an array of numbers. Write a pseudocode for a brute force algorithm, compare with the previous one. Show a tree of the divide and conquer algorithm process. What is the maximum tree level for numbers?

The brute force algorithm is trivial: a loop.
At each level l, the complete binary tree is composed of 2^(l-1) leaves. So the total of the vertices is 2^l -1. Let l be the level of the tree, so l=sup(log_2 (n)).
Exercise 7
Write pseudocode for a divide-and-conquer algorithm for the exponentiation problem of computing a^n where a>0 and n is a positive integer. Write a pseudocode for a brute force algorithm, compare with the previous one. Show a process tree of the divide and conquer algorithm. What is the maximum level of the tree for n not given? Check the termination, accuracy and completeness.
Exercise 8
To multiply two whole numbers of n digits, a naive method consists in multiplying each digit of the first number by each digit of the second, and making the correct offsets and the correct sums. The calculation time is then in O(n²).
Karatsuba's algorithm uses the principle that the calculation used in this naive approach:
(a × 10^k+ b)(c × 10k+ d) = ac × 10^2k+ (ad + bc) × 10^k+ bd
requiring four products (ac, ad, bc and bd) can be done with only three products by grouping the calculations in the following form:
(a × 10^k + b)(c × 10^k + d) = ac × 10^2k + (ac + bd − (a − b)(c − d)) × 10^k + bd
Certainly subtractions have been introduced, but only three products of large numbers are now necessary: ac, bd and (a − b)(c − d).
As additions and subtractions are inexpensive (negligible compared to multiplications), we will save calculation time. For information, multiplication by a power of the calculation base corresponds to a digit shift and is very quick to execute on a machine.
Write the code of the karatsuba() function allowing to multiply two large integers of n digits according to this principle.
Exercise 9
Given a set of real points, find the minimum distance between two points using a Divide and Conquer type algorithm. For this we will use the Euclidean distance between two points.
The obvious solution is to make a distance matrix between each pair of points. The divide and conquer algorithm cuts the space recursively into 2 blocks and looks at the minimum distance in each block. Moreover, it is then necessary to look at the smallest distance between points of two different blocks.
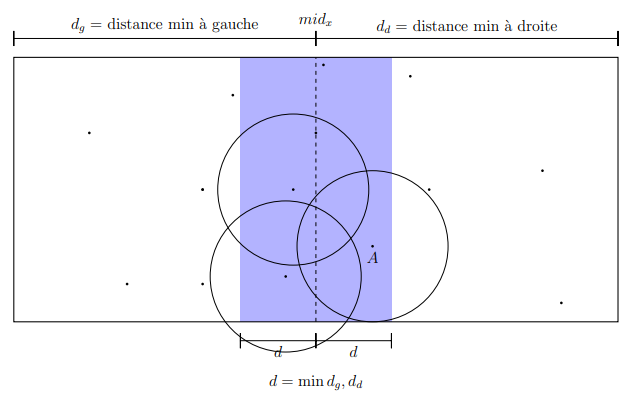
Divide-and-rule solution
— Sort the points relative to their x coordinates.
— Divide the points into two groups: the left half and the right half.
— Use recursion to find dg, the min distance between points of
left.
— Use recursion to find dd, the min distance between line points.
— The optimal solution is:
— either dg,
— either dd,
— let be the distance between two points A and B such that A is in the part
left and B is in the right part.
Let midx be the x coordinate of the rightmost point among the left points. Note that in the third case cited above, the two points A and B are located in a thin band of width min(dg, dd), centered at midx.
We notice in the central band, two points located on the same side of the
midx boundary are at least distance d from each other. This information is used as follows:
— We start by sorting all the points present in the central band according to their y coordinate.
— For each point A in the central band, we look at the distance that separates it from the points located in its radius.

Exercise 10
In this exercise, we are interested in the complexity in the worst case and in the number of comparisons of the algorithms.
1. To find the largest and second largest element of n integers, give a naive algorithm and its complexity.
2. To improve performance, we propose to consider the solution consisting in calculating the maximum according to the principle of Divide and Conquer
1.

2.
The principle is quite simple since it is close to the Merge Sort algorithm. During the reign, a tuple of two elements is raised (max1, max2) or max1 > max2. The reign consists of comparing the left and right tuples and returning the two largest. Thus, each branch will return the two largest of its sub-array until obtaining the two largest of the array in its entirety.
Exercise 11
Given an array of integers, find the maximum sum among all possible subarrays. Sub-arrays must occupy consecutive positions in the original array.
Input: numbers[] = [2, -4, 1, 9, -6, 7, -3]
Output: the maximum sum of the sub-array is 11 (marked in bold)
The idea is to use the Divide and Conquer technique to find the maximum sum of the sub-arrays. The algorithm works as follows:
- Divide the array into two equal sub-arrays.
- Recursively calculate the maximum sum of subarrays for the left subarray,
- Recursively calculate the maximum sum of subarrays for the right subarray,
- Find the maximum sum of the subarray that crosses the middle element.
- Returns the maximum of the above three sums.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 | #include <stdio.h> #include <limits.h> // Utility function to find the maximum of two numbers int max(int x, int y) { return (x > y) ? x : y; } // Function to find the maximum subarray sum using divide-and-conquer int maximum_sum(int nums[], int low, int high) { // If the array contains 0 or 1 element if (high <= low) { return nums[low]; } // Find the middle array element int mid = (low + high) / 2; // Find maximum subarray sum for the left subarray, // including the middle element int left_max = INT_MIN; int sum = 0; for (int i = mid; i >= low; i—) { sum += nums[i]; if (sum > left_max) { left_max = sum; } } // Find maximum subarray sum for the right subarray, // excluding the middle element int right_max = INT_MIN; sum = 0; // reset sum to 0 for (int i = mid + 1; i <= high; i++) { sum += nums[i]; if (sum > right_max) { right_max = sum; } } // Recursively find the maximum subarray sum for the left // and right subarray, and take maximum int max_left_right = max(maximum_sum(nums, low, mid), maximum_sum(nums, mid + 1, high)); // return the maximum of the three return max(max_left_right, left_max + right_max); } int main(void) { int arr[] = { 2, –4, 1, 9, –6, 7, –3 }; int n = sizeof(arr) / sizeof(arr[0]); printf(« The maximum sum of the subarray is %d », maximum_sum(arr, 0, n – 1)); return 0; } |
We can easily solve this problem in linear time using Kadane's algorithm. The idea is to maintain a maximum (positive sum) subarray "terminating" at each index of the given array. This subarray is either empty (in which case its sum is zero) or consists of one element more than the maximum subarray ending at the previous index.
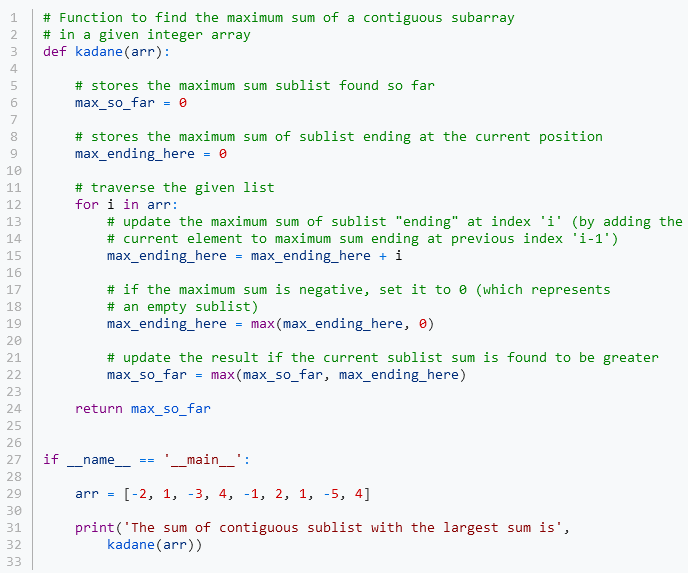
Exercise 12
Given an array of integers, find the peak element it contains. A peak element is an element superior to its neighbors. There can be multiple peak elements in an array and the solution should report any peak element.
An element A[i] of an array A is a peak element if it is not smaller than its neighbor(s).
A[i-1] <= A[i] >= A[i+1] for 0 < i < n-1
A[i-1] <= A[i] if i = n – 1
A[i] >= A[i+1] if i = 0
For instance,
Entry: [8, 9, 10, 2, 5, 6]
Output: peak element is 10 (or 6)
Entry: [8, 9, 10, 12, 15]
Output: peak element is 15
Entry: [10, 8, 6, 5, 3, 2]
Output: peak element is 10
A naive solution would be to test all elements for the spike by running a linear search on the array and returning the element larger than its neighbors. Two particular cases must be treated. If the array is sorted in descending order, its peak element is the first element. If the array is sorted in ascending order, the peak element is last. The problem with this approach is that its worst-case time complexity is O(n), where n is the size of the input.
We can easily solve this problem in O(log(n)) time using an idea similar to the binary search algorithm. The idea is to calculate the median index, and if the middle element is greater than its two neighbors, return the element as it is a peak. If the right neighbor of the median index is greater than the middle element, recursively search for the peak on the right side of the array. If the left neighbor of the middle index is greater than the middle element, recursively search for the peak in the left side of the array.

Exercise 13
Given a sorted array with possibly duplicate elements, the task is to find the indexes of the first and last occurrences of an element x in the given array.
Examples:
Input: tab[] = {1, 3, 5, 5, 5, 5, 67, 123, 125}, x = 5
Output: First Occurrence = 2
Last occurrence = 5
Input: tab[] = {1, 3, 5, 5, 5, 5, 7, 123, 125 }, x = 7
Output: First Occurrence = 6
Last occurrence = 6
The idea to solve this problem is to iterate over the elements of a given array and check the given elements in an array and keep track of the first and last occurrence of the index of the found element .
Run a for loop and for i = 0 to n-1
Take first = -1 and last = -1
When we find an element for the first time, we first update = i
We always update last=i each time we find the element.
We print first and last.

An efficient approach using binary search:
1. For the first occurrence of a number
a) If (high >= low)
b) Calculate medium = low + (high – low)/2;
c) If ((middle == 0 || x > arr[middle-1]) && arr[middle] == x)
middle back;
d) Else if (x > arr[medium])
return first(arr, (middle+1), top, x, n);
e) Otherwise
return first(arr, low, (mid-1), x, n);
f) Else return -1;
2. For the last occurrence of a number
a) if (high >= low)
b) calculate medium = low + (high – low)/2;
c)if( ( middle == n-1 || x < arr[middle+1]) && arr[middle] == x )
middle back;
d) else if(x < arr[middle])
return last(arr, low, (mid-1), x, n);
e) else
return last(arr, (mid + 1), high, x, n);
f) else return -1;

Exercise 14
Given n rectangular buildings in a 2-dimensional city, calculate the skyline of these buildings, eliminating hidden lines. The main task is to view buildings from one side and remove all non-visible sections.
All buildings share a common background and each building is represented by a triplet (left, ht, right)
'left': is the x coordinate of the left side (or of the wall).
'right': is the x coordinate of the right side
'ht': is the height of the building.
A horizon line is a set of rectangular bands. A rectangular strip is represented by a pair (left, ht) where left is the x coordinate of the left side of the strip and ht is the height of the strip.
Examples:
Input: array of buildings
{ (1, 11, 5), (2, 6, 7), (3, 13, 9), (12, 7, 16), (14, 3, 25),
(19, 18, 22), (23, 13, 29), (24, 4, 28) }
Output: Skyline (a set of rectangular strips)
A strip has the x coordinate of the left side and the height
(1, 11), (3, 13), (9, 0), (12, 7), (16, 3), (19, 18),
(22, 3), (25, 0)
The image below is for input 1:

We can find Skyline in time Θ(nLogn) using Divide and Conquer. The idea is similar to Merge Sort, splitting the given set of buildings into two subsets. Recursively construct the horizon for two halves and finally merge the two horizons.
The idea is similar to merging merge sort, start with the first bands of two horizons, compare the x coordinates. Choose the band with the smallest x coordinate and add it to the result. The height of the added strip is taken as the maximum of the current heights of skyline1 and skyline2.
The height of the new strip is always obtained by taking the following maximum
(a) Current height of skyline1, say 'h1'.
(b) Current height of skyline2, say 'h2'
h1 and h2 are initialized to 0. h1 is updated when a SkyLine1 strip is added to the result and h2 is updated when a SkyLine2 strip is added.
Skyline1 = {(1, 11), (3, 13), (9, 0), (12, 7), (16, 0)}
Skyline2 = {(14, 3), (19, 18), (22, 3), (23, 13), (29, 0)}
Result = {}
h1 = 0, h2 = 0
Compare (1, 11) and (14, 3). Since the first band has a smaller left x, add it to the result and increment the index for Skyline1.
h1 = 11, new height = max(11, 0)
Result = {(1, 11)}
Compare (3, 13) and (14, 3). Since the first band has a smaller left x, add it to the result and increment the index for Skyline1
h1 = 13, new height = max(13, 0)
Result = {(1, 11), (3, 13)}
Similarly (9, 0) and (12, 7) are added.
h1 = 7, new height = max(7, 0) = 7
Result = {(1, 11), (3, 13), (9, 0), (12, 7)}
Compare (16, 0) and (14, 3). Since the second band has a smaller left x, it is added to the result.
h2 = 3, new height = max(7, 3) = 7
Result = {(1, 11), (3, 13), (9, 0), (12, 7), (14, 7)}
Compare (16, 0) and (19, 18). Since the first band has a smaller left x, it is added to the result.
h1 = 0, new height = max(0, 3) = 3
Result = {(1, 11), (3, 13), (9, 0), (12, 7), (14, 7), (16, 3)}
Since Skyline1 has no more elements, all remaining elements of Skyline2 are added
Result = {(1, 11), (3, 13), (9, 0), (12, 7), (14, 7), (16, 3),
(19, 18), (22, 3), (23, 13), (29, 0)}
An observation regarding the above output is that the strip (14, 7) is redundant (there is already a strip of the same height). We remove all redundant elements
bands.
Result = {(1, 11), (3, 13), (9, 0), (12, 7), (16, 3), (19, 18),
(22, 3), (23, 13), (29, 0)}
In the code below, redundancy is handled by not adding a band if the previous band in the result has the same height.


Exercise 15
Given an array of integer citations where citations[i] is the number of citations a researcher received for their ith paper and the citations are sorted in ascending order, return to calculate the researcher's h-index.
According to Wikipedia's definition of h-index: a scientist has an h-index if h of his n papers have at least h citations each, and the other n − h papers have no more than h citations each.
If there are several possible values for h, the maximum value is taken as the index h.
Input: quotes = [0,1,3,5,6]
Output: 3
Explanation: [0,1,3,5,6] means that the researcher has 5 articles in total and each of them received 0, 1, 3, 5, 6 citations respectively.
Since the researcher has 3 papers with at least 3 citations each and the other two with no more than 3 citations each, their h-index is 3.
Just binary search, each time check quotes[mid]
case 1: citations[mid] == len-mid, then that means there are citations[mid] articles that have at least citations[mid] citations.
case 2: quotes[mid] > len-mid, then that means there are quotes[mid] articles that have more quotes[mid] quotes, so we should keep looking in the left half
case 3: citations[mid] < len-mid, you must continue the search in the right part
After iteration, right+1 is guaranteed to be the one we need to find (i.e. len-(right+1) papers has at least len-(righ+1) citations)
The following algorithm is written in iterative form but it is Divide and Conquer:

Exercise 16
In the “Koko Eating Bananas” problem, we are given an array of size n that contains the number of bananas in each pile. In one hour, Koko can eat a maximum of K bananas. If the pile contains less than K bananas, then if Koko finishes all the bananas in this pile, she cannot start eating bananas from another pile in the same hour.
Koko wants to eat all the bananas in H hours. We are supposed to find the minimum value of K.
batteries = [30,11,23,4,20], H = 6. Here the answer is 23.

Koko will eat bananas in this way to eat all the bananas in 6 hours:
First hour: 23
Second hour: 7
Third hour: 11
Fourth hour: 23
Fifth hour: 4
Sixth hour: 20
The first and most important thing to solve this problem is to bring out observations. Here are some observations for our search range:
Koko must eat at least one banana per hour. So this is the minimum value of K. let's name it as Start
We can limit the maximum number of bananas Koko can eat in one hour to the maximum number of bananas in a pile among all piles. It is therefore the maximum value of K. Let's call it End.
We now have our search range. Suppose the size of the interval is Length and the number of stacks is n. The naive approach might be to check every value in between. if for this value of K Koko can eat all the bananas in H hour successfully, choose the minimum of them. The time complexity for the naive approach will be Length*n in the worst case.
We can improve time complexity by using binary search instead of linear search. The algorithm is written iteratively but it is indeed a Divide and Conquer approach
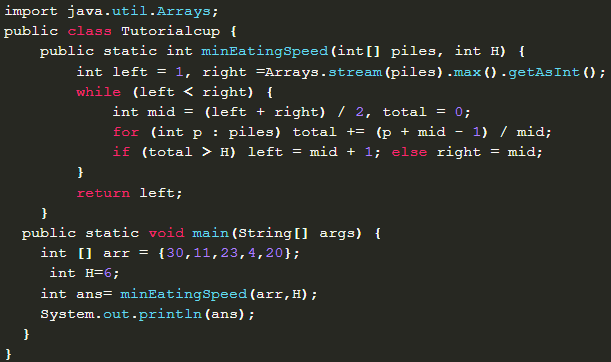
Exercise 17
Given a sorted array of nonnegative distinct integers, find the smallest missing nonnegative element in it.
For instance,
Input: numbers[] = [0, 1, 2, 6, 9, 11, 15]
Result: The smallest missing element is 3
Input: numbers[] = [1, 2, 3, 4, 6, 9, 11, 15]
Output: smallest missing element is 0
Input: numbers[] = [0, 1, 2, 3, 4, 5, 6]
Result: The smallest missing element is 7
A naive solution would be to run a linear search on the array and return the first index, which does not match its value. If no mismatch occurs, return the array size. The problem with this approach is that its worst-case time complexity is O(n), where n is the size of the input. This solution also does not take advantage of the fact that the input is sorted.
We can easily solve this problem in O(log(n)) time by modifying the binary search algorithm (equivalent to Divide and Conquer). The idea is to compare the median index with the median element. If the two are the same, then the mismatch is in the correct subarray; otherwise, it is in the left sub-array. So we discard one half accordingly and come back for the other.
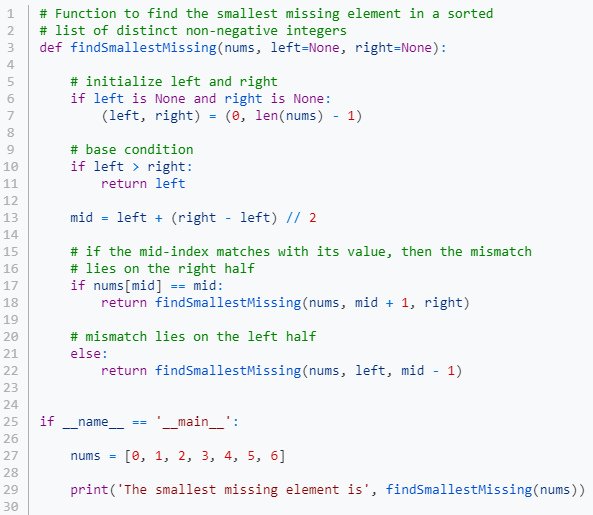
Exercise 18
Given an array of integers nums and an integer k, returns the kth largest element of the array.
Note that this is the kth largest element in sorted order, not the kth distinct element.
You have to solve it in O(nlogn) time complexity.
Example 1:
Input: numbers = [3,2,1,5,6,4], k = 2
Output: 5
Example 2:
Input: numbers = [3,2,3,1,2,4,5,5,6], k = 4
Output: 4
To solve this problem we must go to the simplest. Sort the array in O(nlogn) then iterate through it from largest to smallest. A counter is incremented as soon as we change number, we return the number of the k-th change.
Exercise 19
Given an array of integers nums, return an array of integers counts where counts[i] is the number of smaller elements to the right of nums[i].
Input: numbers = [5,2,6,1]
Output: [2,1,1,0]
Explanation:
To the right of 5 there are 2 smaller elements (2 and 1).
To the right of 2, there is only one smaller element (1).
To the right of 6 there is 1 smaller element (1).
To the right of 1 there is 0 lesser element.
The smallest numbers to the right of a number are exactly those that jump from its right to its left during a stable sort. So I'm doing a merge sort with additional tracking of those jumps from right to left. Here are the algorithms in their iterative form.
We sort the pairs (index, value). The value is used for sorting and the index is used for jump tracking.
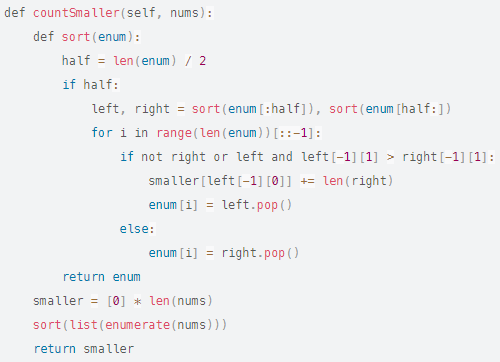
You can also sort indexes only and search actual numbers for on-the-fly comparisons. Maybe a bit easier to understand and port in other languages:

Exercise 20
Given two sorted arrays nums1 and nums2 of size m and n respectively, returns the median of the two sorted arrays.
The overall running time complexity should be O(log (m+n)).
Example 1:
Input: nums1=[1,3], nums2=[2]
Output: 2.00000
Explanation: merged array = [1,2,3] and the median is 2.
Example 2:
Input: nums1=[1,2], nums2=[3,4]
Output: 2.50000
Explanation: merged array = [1,2,3,4] and the median is (2 + 3) / 2 = 2.5.
Let's first look at the concept of 'MEDIAN' in a somewhat unconventional way. That's to say:
“if we cut the sorted array into two halves of EQUAL LENGTHS, then the median is the MEAN OF Max(lower_half) and Min(upper_half), i.e. the two numbers immediately next to the cut”.
For example, for [2 3 5 7], we cut between 3 and 5:
[2 3 / 5 7]
then the median = (3+5)/2.
Here is the Divide and Conquer algorithm:

find the kth element in the two sorted arrays: A[aMid] <= B[bMid], x: mid-length of a, y: mid-length of b, then we can know
(1) there will be at least (x + 1 + y) elements before bMid
(2) there will be at least (m – x – 1 + n – y) = m + n – (x + y +1) elements after aMid
So
if k <= x + y + 1, find the kth element in a and b, but disregard bMid and its suffix
if k > x + y + 1, find the k – (x + 1)th element in a and b, but without considering aMid and its prefix

Exercise 21
Your task is to calculate a^b mod 1337 where a is a positive integer and b is an extremely large positive integer given as an array.
An acquaintance: ab % k = (a%k)(b%k)%k
Since the power here is an array, we'd better handle it digit by digit. A finding :
a^1234567 % k = (a^1234560 % k) * (a^7 % k) % k = (a^123456 % k)^10 % k * (a^7 % k) % k
Does it seem complicated to you? Let me put it another way:
Suppose that f(a, b) computes a^b % k; Then translate the above formula using f:
f(a,1234567) = f(a, 1234560) * f(a, 7)% k = f(f(a, 123456),10) * f(a,7)%k ;
Implementation of this idea:

Exercise 22
To calculate the area under the curve, it is possible to surround the curve with a rectangle and to deduce that the area of the curve is in the order of magnitude of the area of the rectangle.
The method of rectangles is a method algorithmic which makes it possible to obtain a framing of an integral. As a reminder ; a positive function over an interval [a,b], whose integral over this interval is the area under the curve representing f and the abscissa axis.
In the Divide and Conquer algorithm, the interval [a,b] is subdivided into n intervals of width less than a threshold k (k being the calculation precision of the integral).
Let I be the middle of an interval, the area under the curve in this interval is therefore equal to the rectangle whose height is defined by f(I). The area in the original interval is therefore equal to the sum of all the subdivided areas.
It is also possible to bound the area under the curve by considering that it is of the same size as the sum of the rectangles of height f(a) and of the same size as the sum of the rectangles of height f(b).
A third method exists to simulate the area under the curve: the trapezium method.
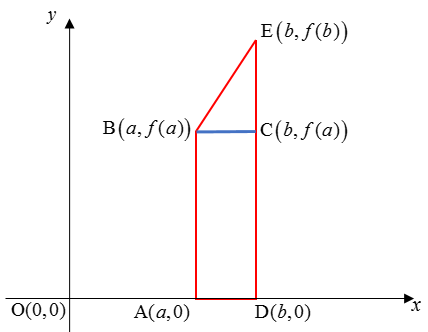
To calculate the area of the trapezium ABED, we add the areas of the rectangle ABCD and the right triangle BEC. The area of the trapezium is a representation of the area under the curve in the interval [a,b].
The algorithms are very simple. As long as the threshold size is not reached, we return method(a, (a+b)/2, function) + method ((a+b)/2, b, function).
This calculation makes it possible to sum the left and right parts of the divide of the interval. Once the threshold has been reached, the method returns the calculation of the area corresponding to the statement studied.
For the rectangles said to the right we will have as total sum:
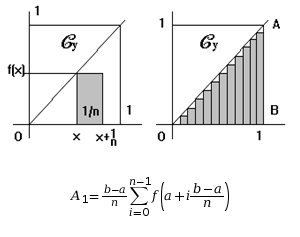
For the rectangles said to the left we will have as total sum:

For the trapezium method, the calculation of each sub-interval is given by the following formula: