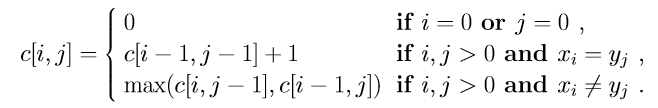Contents
ToggleCorrected exercises about Divide & Conquer and Dynamic programming
This page purposes several corrected exercises about algorithms, more particularly on Divide & Conquer paradigm and dynamic programming.
Exercise 1
Write a pseudocode for a divide-and-conquer algorithm for finding the position of the largest element in an array of numbers. Write a pseudo code for a brute-force algorithm, compare with the previous one. Show a tree of the divide-and-conquer algorithm's process. What is the max level of the tree for numbers?

The brute-force algorithm is trivial: a loop.
At each level l, the complete binary tree is composed of 2 ^ (l-1) leaf. So the total of vertices is 2 ^ l -1. Let l be the level of the tree, so l = sup (log_2 (n)).
Exercise 2
Write a pseudo code for a divide-and-conquer algorithm for the exponentiation problem of computing a ^ n where a> 0 and n is a positive integer. Write a pseudo code for a brute-force algorithm, compare with the previous one. Show a tree of the divide-and-conquer algorithm's process. What is the max level of the tree for n not given? Verify termination, correctness and completeness.
Exercise 3
You are given an array with integers (positive, negative, zero) and you are supposed to find the maximum contiguous sum in this array. Hence, you have to find a sub-array which results in the largest sum. Example, if the given array is: 5, -6, 7, 12, -3, 0, -11, -6
Assume your input array is called A. What you need to do is form another array, say B, whose each value i is calculated by using the recursive formula, max (A [i], B [i-1] + A [i ])
What you are doing effectively is that you are choosing whether to extend the earlier window or start a new one. You can do this since you are only supposed to select continuous elements as part of your subsets.
5, -6, 7, 12, -3, 0, -11, -6
The answer would be, 19 (from the sub-array {7,12})
Exercise 4
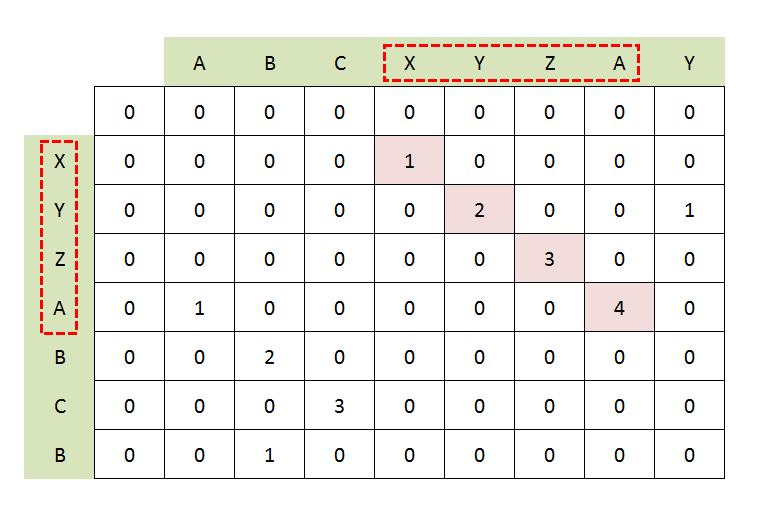
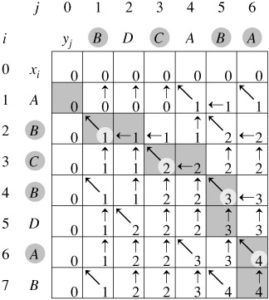
Use the Longest Common Substring for: BDCABA and ABCBDAB

Exercise 5
Adapt the Longest Common Substring to the Longest Common Subsequence: BDCABA and ABCBDAB. The longest common subsequence (LCS) problem is the problem of finding the longest subsequence common to all sequences in a set of sequences (often just two sequences).
It differs from problems of finding common substrings: unlike substrings, subsequences are not required to occupy consecutive positions within the original sequences.
Exercise 6
The Levenshtein distance is a string metric for measuring the difference between two sequences. Informally, the Levenshtein distance between two words is the minimum number of single-character edits (ie insertions, deletions or substitutions) required to change one word into the other. Offers a dynamic program to solve this problem. Test with MEILENSTEIN and LEVENSHTEIN.