Contents
ToggleRecursive programming
The structure of a algorithm recursive is:
algo () {condition 1 condition 2 ... condition n}The conditions are generally ifs, they include the stop conditions (does not return the function) or continuity conditions (relaunches the function or returns the function). The continuity conditions modify the inputs of the restarted function. A recursive function must have at least one stop condition.
Simple recursion
The mathematical program is of the following type (example for the calculation of a power):
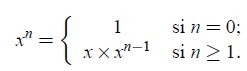
Here is a simple example to calculate the factorial of n:
int fact (n) {if (n == 0) return 1; else return n * fact (n-1); }Here we can see the fact that recursion behaves like a loop.
Multiple recursion
The mathematical program is of the following type (example for Pascal's relation):
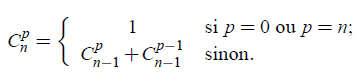
Will give for program:
int pascal (n, p) {if (p == 0 || p == n) return 1; else return pascal (p, n-1) + pascal (p-1, n-1); }Other types
Two algorithms are “mutually” recursive if one calls on the other and vice versa.
An algorithm contains a "nested" recursion if a parameter of the recursion is a call to itself.
Execution stack
The stack of execution of the current program is a memory location intended to memorize the parameters, the local variables as well as the return addresses of the functions being executed.
This stack works according to the LIFO (last in first out) principle and has a fixed size. Here is the stack for the simple factorial, as soon as the program reads a method, it executes it, keeping the rest of the information on the stack, and it adds the new results to the top of the stack. Since it is LIFO, this last piece of information will then be read first, which is why it gives the impression of an execution pyramid:
Call to fact (3) 3 * fact (2) Call to fact (2) 2 * fact (1) Call to fact (1) 1 * fact (0) Call to fact (0) Returns the value 1 Returns 1 * 1 Returns 2 * 1 Returns 3 * 2 Returns 6
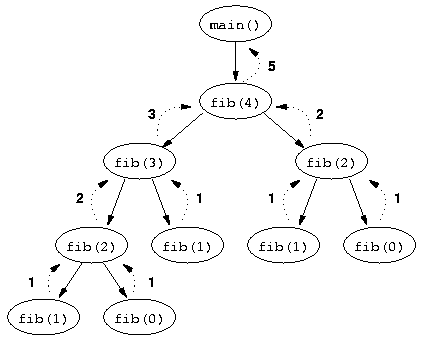
The Fibonacci sequence execution stack follows the same principle:
int fibo (n) {return (n <2)? 1: fibo (n-1) + fibo (n-2); }Fibo (3) Fibo (2) + wait Call to Fibo (2) Fibo (1) + wait Call to Fibo (1) Returns 1 1 + Fibo (0) Call to Fibo (0) Returns 1 Returns 1 + 1 2+ Fibo (1) Call to Fibo (1) Returns 1 Returns 2 + 1 Returns 3
We clearly see here a roller coaster effect due to the successive popping of the function on the left as soon as it is encountered. It is easier to represent the stack of a multiple recursive function by a in-depth journey (we go the farthest in the successors) of its recursive call tree:
Terminal recursion
Thus, the stack has nothing in memory throughout the recursion. This means that the returned value is directly the value obtained without there being any additional operation. Let us take the example of the factorial in a terminal recursive way:
int fact (n, a) {if (n == 0) return a; else return fact (n-1, n * a); } // be careful, the value of a at the start is very importantThis is exactly the same as writing the following loop:
while (n! = 0 {n * = a; n--;}