Contenido
PalancaModelo matematico
El modelado matemático es la base de todo trabajo de ingeniería. El modelado matemático se caracteriza por tres conceptos:
- La presencia de elección, que se hará entre un conjunto finito (noción que se puede comparar con la teoría de probabilidades)
- Un principio de restricciones que define el conjunto finito de opciones.
- Un principio de evaluación de las opciones disponibles.
Modelado matemático de un problema
Las cuatro etapas del modelado matemático de un problema industrial son las siguientes:
- ¿Cuáles son los datos del problema? recopile los datos del problema, comprenda el problema;
- ¿Cómo modelar el problema? los tres puntos de laayuda con la decisión
- ¿Qué decisiones tenemos que tomar? seleccionar / colocar objetos, definir un pedido o cantidad, elegir un evento, realizar una operación en particular;
- ¿Cuáles son las limitaciones del problema? respetar las capacidades o las limitaciones de precedencia;
- ¿Cuál es el objetivo que se busca? maximizar las ganancias, minimizar los costos o la cantidad;
- Cuál es la complejidad de este problema? polinomio, Np, Np-difícil;
- Como resolver el problema ? diseñar algoritmos (exactos vs aproximados) que brinden soluciones factibles / óptimas, desarrollar métodos alternativos o híbridos
Dependiendo del modelo matemático, el modelo también puede servir como simulación. Entonces es posible ver el impacto de ciertas decisiones en un contexto diferente al estudiado (como el estudio de la sensibilidad del símplex).
Toma de decisiones y modelado matemático
La toma de decisiones durante el modelado matemático implica tres fases principales seguidas de la fase de validación:
- Recabando información: Examinar e identificar el problema (variables, funciones, valores, etc.).
- Identificando el problema: Identificación de metas y objetivos organizados relacionados con un problema. Para determinar si existe un problema, identifique sus síntomas, determine su alcance y defínalo explícitamente. Pueden surgir algunos problemas durante la recopilación y estimación de datos, como falta de datos, datos imprecisos o inexactos, estimación deficiente, sobrecarga de información, datos simulados, etc.
- Clasificación del problema: La clasificación del problema es la ubicación de un problema en una categoría definible. Esto conduce a un enfoque de solución estandarizado.
- Desglose de problemas: Muchos problemas complejos se pueden dividir en subproblemas. Algunos problemas no estructurados pueden tener subproblemas muy estructurados.
- Diseño: Construya un modelo que represente el sistema.
- Entender el problema: El modelado implica la abstracción del problema en formas cuantitativas y / o cualitativas.
- Se construye, se prueba y se valida un modelo: Para un modelo matemático, se identifican las variables y se establecen las relaciones entre ellas. Todos los modelos se componen de tres componentes básicos: variables de decisión, variables no controlables y variables de resultado. Las relaciones Matemáticas unir estos componentes. En un modelo no cuantitativo, las relaciones son simbólicas o cualitativas.
- Opcion: Para seleccionar una solución al modelo.
- Recomendación de una solución: Cuando se resuelve el problema, se elige una solución basada en el modelo. Esto se recomienda para todas las soluciones.
- Evaluar una solución: La evaluación es posible si las variables de resultado dan una solución cuantitativa. Una relación de preferencia sobre la solución completa da un orden: f (a) ⪯ f (b) significa que f (b) es mejor o igual af (a) donde a, b son variables yf (.) Es una función matemática basado en las variables de resultado. b es la mejor solución sif: f (x) ⪯f (b) para todo x en el conjunto de la solución.
- Implementación: Implementar software para resolver cualquier instancia de modelado matemático.
- Implementación clásica / iterativa: Los algoritmos iterativos utilizan construcciones repetitivas como bucles y, a veces, estructuras de datos adicionales como pilas para resolver problemas determinados.
- Recursividad: a algoritmo recursivo es un algoritmo que se refiere a sí mismo repetidamente hasta que una condición de terminación partidos.
- Lógica: un algoritmo lógico se compone de un componente lógico y un componente de control.
- Determinista o no determinista: los algoritmos deterministas resuelven el problema con una decisión exacta en cada paso del algoritmo, mientras que los algoritmos no deterministas resuelven los problemas "adivinando". Un algoritmo determinista es un algoritmo que, dada una entrada en particular, siempre producirá la misma salida.
- Exacto o aproximado: Si bien muchos algoritmos alcanzan una solución exacta, los algoritmos de aproximación buscan una aproximación cercana a la verdadera solución. Cuando no es posible encontrar la mejor solución en tiempo humano, podemos buscar una solución aproximada por algoritmos menos complejos.
- Serie, paralelo o distribuido: estas implementaciones dependen de las arquitecturas de la computadora, es decir, del número de procesadores que pueden trabajar en un problema al mismo tiempo, y de cómo descomponer todo el proceso en procesos independientes.
- Paradigma: Fuerza bruta; Divide y conquistaras; Programación dinámica; Buscar; aleatorizado; Reducción. Luego, debemos verificar la terminación, la corrección y la integridad del algoritmo.
- Validación: Validar el software si presenta un tiempo de cómputo razonable y una buena solución.
- La complejidad del mejor caso: Ésta es la complejidad para resolver el problema de la mejor entrada de tamaño n.
- La complejidad del peor de los casos: Ésta es la complejidad para resolver el problema de la peor entrada de tamaño n.
- Complejidad media de casos: Es la complejidad de resolver el problema en promedio. Esta complejidad solo se define con respecto a una distribución de probabilidad en las entradas. Por ejemplo, si se supone que todas las entradas del mismo tamaño tienen la misma probabilidad de aparecer, la complejidad promedio de los casos se puede definir en relación con la distribución uniforme sobre todas las entradas de tamaño n.
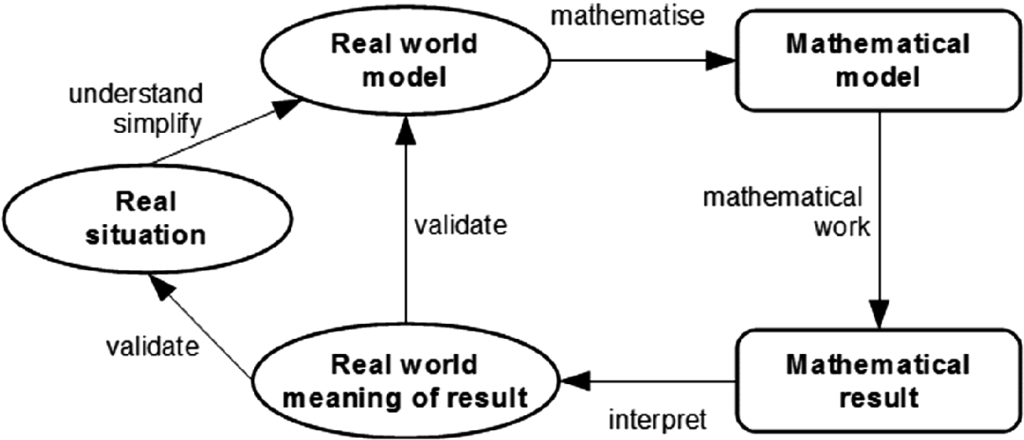
El siguiente diagrama muestra el proceso de modelado matemático: