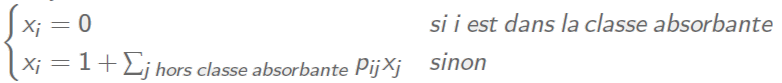Contenido
PalancaAbsorción de un estado
A cadena de markov es absorbente (absorción de un estado) si y sólo si: hay al menos un estado absorbente, de cualquier estado no absorbente se puede llegar a un estado absorbente. Para cualquier cadena de Markov absorbente y para cualquier estado inicial, la probabilidad de estar en un estado absorbente en el tiempo t tiende a 1 cuando t tiende a infinito.
Cuando se trata de una cadena de Markov absorbente, generalmente nos interesan las dos preguntas siguientes:
- ¿Cuánto tardará en promedio en llegar en estado absorbente, dado su estado inicial?
- Si hay varios estados absorbentes, ¿cuál es la probabilidad de caer en un estado absorbente dado?
Si una cadena de Markov es absorbente, colocaremos los estados absorbentes al principio; nosotros
entonces tendrá una matriz de transición de la siguiente forma (I es una matriz unitaria y 0
una matriz de 0):

La matriz N = (IQ)-1 se llama la matriz fundamental de la cadena absorbente. Considere la siguiente matriz estocástica:
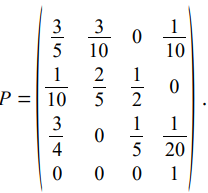
Luego tenemos que calcular N:
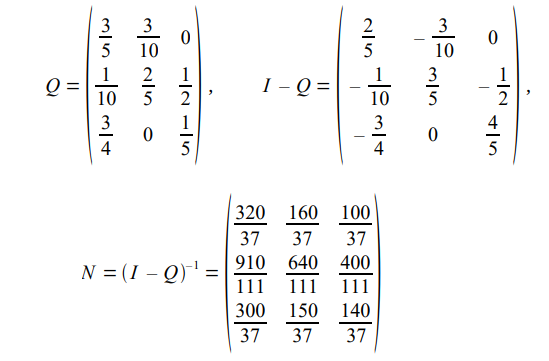
El número medio de pasos antes de la absorción sabiendo que partimos del estado i (no
absorbente) es la suma de los términos de la i-ésima fila de N.
En el ejemplo anterior, el número medio de pasos antes de la absorción se toma de la primera línea, comenzando desde el estado 1: 320/37 + 160/37 + 100/37 = 15,67.
En el mismo ejemplo:
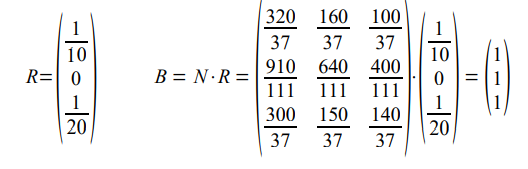
La probabilidad de ser absorbido por el estado absorbente único es 1, sea cual sea el estado inicial.
Ecuaciones lineales
Desde el punto de vista de una ecuación lineal, el vector de probabilidades de absorción es la solución positiva más pequeña del sistema:

El vector de tiempo medio para llegar es la solución positiva más pequeña del sistema: