LP: forma canónica y forma estándar

Forma canónica y forma estándar

Los programas lineales siguen ciertas reglas al escribirlos. A programa lineal que sigue las reglas se dice que está en forma canónica. el algoritmo de símplex solo se puede aplicar a programas lineales en la forma canónica.

Forma canónica

Un programa lineal en su forma canónica es:

• Un problema de maximización, bajo restricciones inferiores o iguales, cuyas variables son estrictamente positivas.
• un problema de Minimización, bajo restricciones mayores o iguales, todas cuyas variables son estrictamente positivas.

Si el programa lineal no se corresponde con estos criterios, es necesario transformar las restricciones o la función objetivo de acuerdo con las siguientes operaciones:

• max z = - min -z
• x + y ≥ b es equivalente a - x - y ≤ - b
• x + y = b es equivalente ax + y ≥ b, x + y ≤ b

La forma canónica a menudo se representa en forma de matriz:

• el vector de los coeficientes de la función objetivo: c de tamaño n
• la matriz de los coeficientes de la parte izquierda de las restricciones: A de tamaño m * n
• el vector de las constantes de la parte derecha de las restricciones: b de tamaño m
• el vector de variables: x de tamaño n

De ahí el siguiente programa lineal:

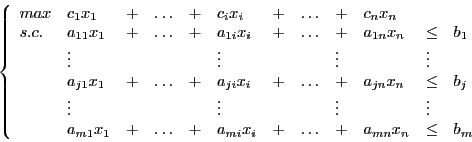
Escrito en la siguiente forma:

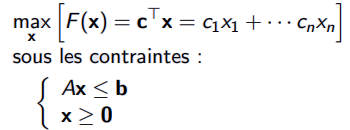
Forma estándar

Para cada restricción de desigualdad de la forma canónica, agregamos un variable de holgura positivo y tal que:

Ax ≤ b ⇔ Ax + e = b, e ≥ 0, aquí e es un vector de tamaño m de variables de desviación.

Por lo tanto, la forma canónica se lleva a la forma estándar mediante la adición de las variables de variación en el vector de variables:

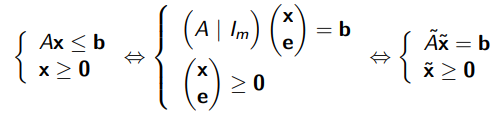
• el vector de los coeficientes de la función objetivo: c de tamaño n + m (n para xym para e aunque estos últimos no entran en el cálculo)
• la matriz de los coeficientes de la parte izquierda de las restricciones: Ã de tamaño m * (n + m), siendo la parte derecha de la matriz una matriz de identidad de tamaño m.
• el vector de las constantes de la parte derecha de las restricciones: b de tamaño m
• el vector de variables de tamaño n + m

Algunas desigualdades no permiten tener variables de base positivas. Para ello debemos sumar otras variables llamadas variables de exceso y artificiales.

Aquí están las reglas a seguir para transformar mejor el simplex en forma estándar:

• Restricciones “mayor o igual” o “menor o igual con b negativo”: haga que b sea positivo y agregue “– variable de holgura + variables artificiales »
• Restricciones de "igualdad": agregue "+ variable artificial"
• restricciones "menor o igual que con b positivo": agregue "+ variable de variación" como se vio anteriormente.