Contenido
PalancaEjercicios de programación lineal corregidos (forma primaria)
Este tutorial ofrece varios ejercicios corregidos sobre modelado en forma básica de programación lineal.

Tutorial
Un fabricante de herramientas de fresado fabrica dos tipos de cortadores: A y B. Los cortadores tipo A se venden a 300 cada uno y se fabrican con 1 unidad de acero, 2 unidades de carburo removible y 1 unidad de diamante sintético. Los cortadores tipo B se venden a 200 cada uno y están hechos con 2 unidades de acero, 1 unidad de carburo removible y 1 unidad de diamante sintético.
Las existencias son 5 unidades de acero, 5 unidades de carburo y 2 unidades de diamante. El fabricante quiere construir al menos 5 cortadores tipo A y 5 cortadores tipo B. El costo de mantenimiento de la fábrica es de 2500. ¿Cómo debe distribuir el fabricante su producción para maximizar sus ganancias, es rentable?
Primero, se debe realizar el programa lineal:
- Función objetivo: z = 300A + 200B-2500
- Restricciones:
- A + 2B ≤ 5
- 2A + B ≤ 5
- A + B ≤ 2
- A ≥ 5
- B ≥ 5
El programa no está en forma canónica, debe renderizarse en esta forma antes de resolverlo.
Sea x1 = A-5 y x2 = B-5. El programa lineal se convierte en el siguiente:
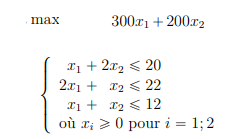
El programa lineal tiene 2 variables, por lo que es posible resolverlo gráficamente. Las restricciones dan el dominio de las siguientes soluciones:
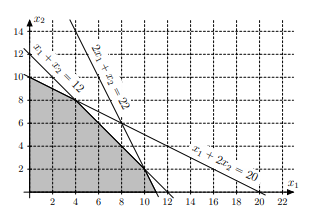
El gradiente de la función objetivo es (3,2), que da como punto final la intersección de la segunda y tercera restricción. Por tanto, debemos resolver el sistema:

Que tiene por solución el vector (10, 2). Esto da en el problema inicial el vector (15, 7) y para la función objetivo igual a 900. La operación es positiva y por lo tanto rentable para la fábrica.
Ejercicio 1
Un corredor necesita, para sus clientes, 108 MWh de electricidad para la ciudad 1 y 96 MWh de electricidad para la ciudad 2. Sin embargo, las leyes de Kirchhoff no permiten que un distribuidor apunte a una sola ciudad para el tránsito de energía. Dos distribuidores atienden estas ciudades: el distribuidor A puede enviar 12 MWh a la ciudad 1 y 8 MWh a la ciudad 2 por lote comprado; El distribuidor B puede enviar 9 MWh a la ciudad 1 y 12 MWh a la ciudad 2 por lote comprado. Todos los lotes tienen el mismo precio. ¿Cuántos lotes debe comprar el corredor para satisfacer la demanda de energía de las dos ciudades? Resuelve por método gráfico.
El programa lineal es el siguiente: X1 para el primer lote y X2 para el segundo lote
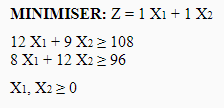
Lo que da por resolución gráfica:
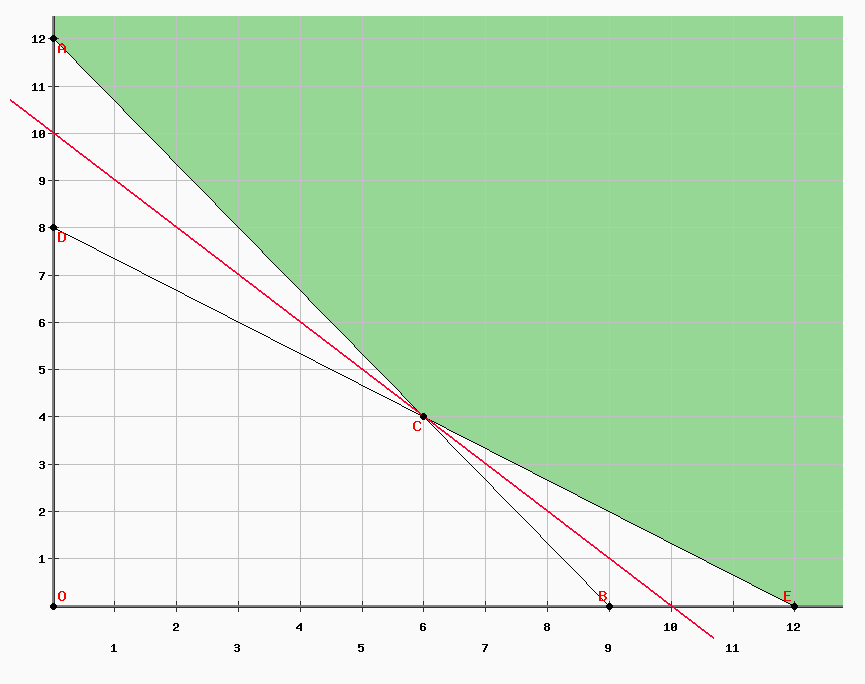
El gradiente es (-1, -1) porque es un mínimo (min f (x) = - max -f (x)). En el campo de la definición en verde, el punto C es el único extremo que es un óptimo global. Resolver el sistema anterior en forma de igualdad da las coordenadas (6, 4) con Z = 10.
Ejercicio 2
Resolver por el método gráfico y luego por el simplex los siguientes problemas:
- Una empresa que fabrica dos tipos de productos busca maximizar su beneficio. Aquí está su hoja de ruta.
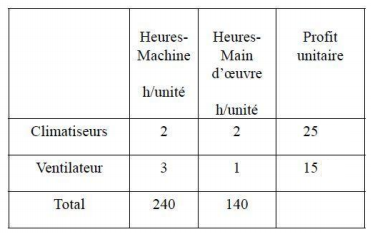
- Así mismo con el siguiente programa lineal:

La metodología es siempre la misma para la parte de resolución gráfica. Aquí están las correcciones de los símplex con el estado inicial y el estado final de la tabla para el primer ejemplo.
Problema 0:

Y para la solución:

La función objetivo tiene para el valor Z = 1875 con P1 y P2 en base (por lo tanto, no cero) teniendo respectivamente para el valor (25,15) como se estipula en la columna b representada por P0.
El segundo programa lineal tiene como solución Z = 8.2 con el vector de variables básicas (3.2, 1.8).
Ejercicio 3
BIM optimiza la construcción, rehabilitación y mantenimiento de edificios. Entre los elementos a optimizar están los trabajadores. En general, hay 4 tipos de trabajadores según su fin de semana. Los salarios de los trabajadores dependen de estos días de licencia:

Las demandas diarias de los trabajadores son las siguientes:

¿Cuántas personas de cada categoría deben emplearse para satisfacer la demanda y minimizar el costo de personal? Da la forma canónica del problema y resuélvelo usando Solver Excel.
El programa lineal es el siguiente:
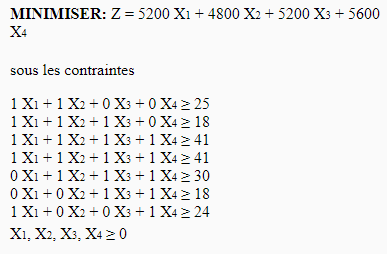
La resolución de Excel es la siguiente:

El resultado es el siguiente:

Tenga en cuenta que la solución óptima no es única. La solución da números enteros, lo cual es práctico dado el problema (parece obvio que se necesitan individuos "enteros").
Ejercicio 4
Una empresa fabrica tres tipos de productos, A, B y C. Cada producto requiere materias primas y mano de obra, así como espacio de almacenamiento. Aquí están las necesidades de materia prima, mano de obra y almacenamiento para una unidad de cada uno de los 3 tipos de productos:
- Producto A: 4 kg de materias primas, 2 horas de mano de obra, 1 unidad de volumen.
- Producto B: 2 kg de materias primas, 1/2 hora de trabajo 1 unidad de volumen.
- Producto C: 1 kg de materia prima, 3 horas de mano de obra, 1 unidad de volumen.
Cada producto aporta 6 euros si es de tipo A, 2 euros si es de tipo B y 4 euros si es de tipo C. Los recursos disponibles son 6000 kg de materias primas, 4000 horas de mano de obra. 2.500 unidades de volumen de almacenamiento.
Modele el programa lineal y resuélvalo a mano usando el simplex.
Un competidor, que carece de materias primas, ofrece comprar 300 kg a esta empresa, a un precio de 1,5 euros el kg. ¿Cree que la empresa debería aceptar esta propuesta? (Suponga que lo acepta si le resulta rentable, resuelva el problema a mano con el simplex).
El problema en forma estándar es el siguiente:

Con la solución simplex:

El problema de redención tiene adicionalmente en la función objetivo 450. La primera variable tiene para el elemento b = 5700. En este caso, la solución óptima es (1310, 0, 460) con Z = 10150, por lo que la proposición es rentable.
Ejercicio 5
Una empresa fabrica tres tipos de baterías: tipo seco 1 (PS1), tipo seco 2 (PS2) y combustible (PC). El proceso de fabricación tiene tres etapas: montaje, prueba de calidad, tratamiento de aislamiento. Solo las baterías que pasan la prueba de calidad se someten al tratamiento de aislamiento. Las baterías que no superan la prueba de calidad se desechan. Durante el próximo mes, la empresa dispondrá de 9.000 horas de tiempo de máquina para el montaje, 1.200 horas para las pruebas de calidad y 8.500 horas para el procesamiento del aislamiento. La siguiente tabla resume la información relevante del proceso de fabricación:

¿Cuál es la cantidad óptima de baterías de cada tipo para fabricar el próximo mes si la empresa está segura de vender toda su producción?
Sean X1, X2, X3 las tres variables que representan el número de pilas válidas de cada tipo y X4, X5, X6 las tres variables que representan el número de pilas inválidas de cada tipo.
El programa lineal en forma canónica es el siguiente:
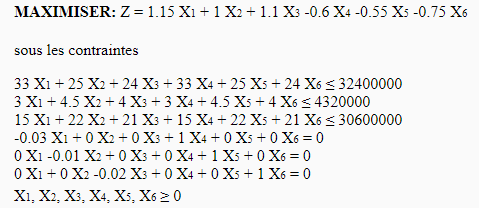
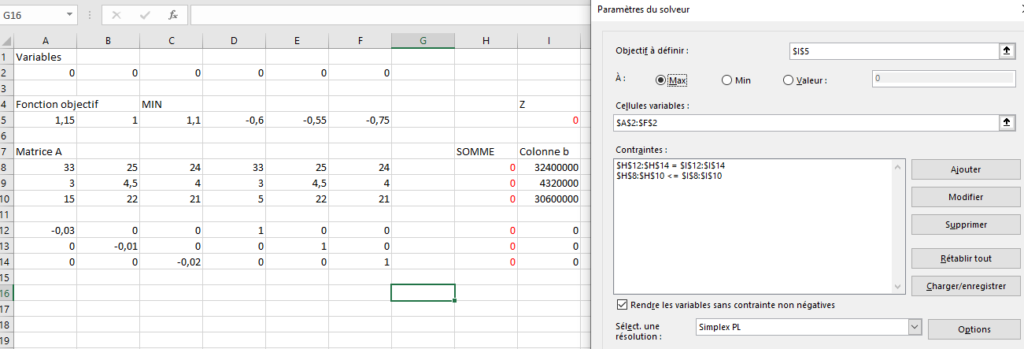
Esto da como solución (419417.476, 0, 741176.471) para baterías válidas y para la función objetivo Z = 1278957.05. Como la solución no da un resultado entero, es posible truncar la parte flotante (¡cuidado, ya no será una solución óptima!).
Ejercicio 6
En una red eléctrica, la cantidad de energía que puede pasar de las centrales eléctricas a las ciudades está limitada por las capacidades de las líneas de muy alta tensión. El problema se describe de la siguiente manera:
- Las fuentes, representadas por vértices, producen una cantidad de energía
- Los pozos, representados por vértices, reciben una cantidad de energía
- Líneas, representadas por aristas entre un par de vértices, por donde pasa la energía.

Este gráfico dice lo siguiente:
- S es una fuente ficticia, que describe la producción de las fuentes de energía representadas por el vértice 1 y el vértice 2.
- T es un pozo ficticio, que describe la recepción de energía de las ciudades representadas por el vértice 3 y el vértice 4.
- Las líneas están orientadas, es decir que la energía solo pasa en una dirección. Por ejemplo, el enlace (1, 3) puede circular hasta 4 unidades de energía entre el vértice 1 y el vértice 3.
- Los vínculos entre S y las fuentes describen la producción de energía de la fuente. Por ejemplo, el enlace (S, 1) dice que la fuente 1 puede producir hasta 10 unidades de energía.
- Los vínculos entre los pozos y T describen la demanda de energía del pozo. Por ejemplo, el enlace (3, T) dice que la ciudad 3 requiere 10 unidades de energía.
La función objetivo de este tipo de problemas es:
- maximizar la cantidad de energía que se puede hacer pasar de S a T. La solución proporcionará la cantidad de energía que pasa por cada línea. Para calcular este flujo, se agrega un arco entre el pozo ficticio y la fuente ficticia no restringida. La solución óptima es igual al flujo que pasa por este arco.
Este problema está sujeto a dos tipos de restricciones:
- la suma de las energías que entran en un vértice menos la suma de las energías que salen del mismo vértice es cero. Es decir que no hay pérdidas de energía en la red.
- la energía que pasa a través de una línea no puede ser mayor que la capacidad de la línea.
- la energía que pasa por una línea es positiva o nula.
Por tanto, las variables son:
- para cada fila, una variable describe la cantidad de energía que la atraviesa.
Formule el problema lineal para el gráfico anterior y resuélvalo a través de Excel.
El problema lineal está escrito en Excel de la siguiente manera:

Lo que da como resultado:

