Contenus
ToggleExercices corrigés : algorithme récursif
Les exercices corrigés suivants concernent le principe d’algorithme récursif, par exemple Fibonacci, les tours de Hanoï et bien d’autres cas mathématiques. Les exercices comprennent la récursion simple, la récursion terminale, la récursion croisée ou récursion mutuelle, et le principe de mémoïsation (pour plus de détail sur ce dernier point merci d’aller voir le principe de programmation dynamique).

Exercice 1
Réécrire les algorithmes suivants sous forme récursive sous forme terminal quand c’est possible.



Un dernier pour la route. Cette fois il faut comprendre ce qu’il fait avant de le rendre récursif terminal !

On considère que n est un entier positif ou nul.


algo3 est déjà récursif mais non terminal. Puisque l’algorithme renvoit 2^n, on va changer sa structure pour le rendre terminal.

Pour le dernier algorithme, il faut d’abord comprendre qu’il calcule le pgcd entre a et b. Faites un test à la main, vous comprendrez que le premier embranchement ne sert à rien, on va donc l’enlever pour la récursion. La variable r n’est pas présente pour remplacer la valeur de a et b, donc elle ne rentrera pas dans la récursion.

Exercice 2
Le problème de Fibonacci (1170 – 1250) :
« Possédant initialement un couple de lapins, combien de couples obtient-on en douze mois si chaque couple engendre tous les mois un nouveau couple à compter du second mois de son existence ? Les lapins ne meurent jamais.”
Donc si on prend un exemple les 7 premiers mois.
Mois | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Couple | 1 | 1 | 2 | 3 | 5 | 8 | 13 |
a – Exprimez la population de couples du mois n en fonction des mois précédents.
b – Ecrire un algorithme itératif qui calcule le nombre de couples au bout de 12 mois.
c – Modifier l’algorithme itératif pour calculer le nombre de mois au bout duquel la population de couples de lapins dépasse 300.
d – Ecrire l’algorithme récursif pour calculer le nombre de couples de lapins après n mois.
a –
Le nombre de couples de lapins au mois n est la somme des couples existants le mois d’avant (au mois n − 1) et des couples naissants au mois n.
Or, le texte précise que tous les couples existants deux mois auparavant (au mois n − 2) se reproduisent.
Par conséquent, au mois n ≥ 2 le nombre de lapins est égale à la somme du mois n-1 et n-2. Au mois 0 et au mois 1, il n’existe qu’un seul couple.
b –

c –

d –

Il est possible de faire Fibonacci sous forme terminale :

Ou alors en utilisant la mémoïsation :

Exercice 3
a – Ecrire un algorithme qui calcule le maximum de 2 nombres réels
b – Ecrire un algorithme récursif qui calcule le maximum de 3 nombres réels en utilisant l’algorithme du a. Montrer l’arbre d’appels.
c – Ecrire un algorithme récursif qui calcule le maximum de 4 nombres réels en utilisant l’algorithme du a. Montrer l’arbre d’appels.
d – L’algorithme est-il récursif ?
a –

b –

Ici, Maximum2 fait office de condition terminal de l’algorithme récursif. La pile d’appels est la suivante :

c –

La pile d’appels est la suivante :

d – Bien qu’on ait l’impression de faire une récursion, il s’agit plutôt d’une surcharge de fonction ou d’appel de fonction pour réduire la taille du problème. Ce n’est pas un algorithme récursif à proprement parler.
Exercice 4
a – Est-ce que les algorithmes ci-dessous sont des algorithmes récursifs ?
b – Est-ce qu’ils sont terminaux ?
c – Est-ce qu’ils se terminent ?



a –
Les algorithmes log et somme sont récursifs : chacun contient au moins un appel à lui même, par contre, puissance ne l’est pas : il fait appel à l’algorithme puis. Il faut remplacer puis par puissance.
b –
log est terminal, puissance et somme ne le sont pas car ils demandent un calcul lors de la récursion.
c –
log se termine pour tout entier x. L’itération de la division entière par 2 mène à 0, et le cas de base 0 se termine par l’exécution de retourner.
Pour l’algorithme puissance (corrigé), le cas de base 0 se termine par l’excéution de retourner. Si l’algorithme se termine pour la valeur n−1 alors il se termine aussi pour la valeur n est exécutant retourner. N’oubliez pas qu’un utilisateur peut rentrer n’importe quoi comme puissance(2, – 5) donc il faut bien vérifier sa terminaison.
somme ne se termine pas lorsque n est strictement positif. En effet, l’algorithme pour n se termine seulement si l’algorithme se termine pour n+1. Or, il n’existe pas d’entier strictement positif pour lesquels l’agorithme s’arrête.
Exercice 5
a – On souhaite écrire une fonction récursive qui calcule le carré d’un entier. Pour cela il va falloir se servir d’une relation entre carre(n) et carre(n-1) sachant que carre(1)=1. Représenter la pile d’appels pour carre(5).
b – Les combinaisons sont un concept de mathématiques décrivant les différentes façons de choisir un nombre donné d’objets dans un ensemble de taille donnée. Par exemple combien il est possible de tirer 6 boules de Loto sur 60 dans le moulinet. Ou de piocher 3 cartes dans un jeu de tarot. La combinaison de choisir p éléments parmi n éléments se notent C(p,n)=(n/p)*C(p-1, n-1). On a aurri C(0,n)=1 et C(n,n)=1.
Ecrire la fonction récursive non terminale puis la fonction récursive terminale, et montrer la pile d’appels pour C(3,7). Via la fonction terminale, en déduire la fonction itérative.
c – Pour les combinaisons, on préfère généralement éviter la méthode du b car les divisions peuvent créer des problèmes d’arrondis. On va plutôt se servir de la relation suivante : C(p,n)=C(p,n-1)+C(p-1, n-1). Ecrire la fonction récursive et la pile ou arbre d’appels pour C(2,4).
a – Pour trouver un lien entre carre(n) et carre(n-1), on utilise la formule : (n+ 1)² = n² + 2n+ 1. On l’écrit en fonction de n vers n-1 : n² = (n−1)²+2(n−1)+1 d’où carre(n)=carre(n-1)+2*n-1. Le tour est joué !

La pile d’appels est :

b – Tout est dit dans l’énoncé, il ne reste qu’à l’écrire.

Voici la liste d’appels pour C(3,7) :

Et maintenant pour la version terminale, c’est un peu plus compliqué car il faut se questionner sur ce qu’on doit garder en mémoire pour la récursion. A chaque itération on a fait n/p fois le précédent, donc n/p * (n-1)/(p-1). On aurait pu l’écrire n(n-1)/p(p-1). Donc on pourrait stocker d’un côté la multiplication de n décroissant et de l’autre de p décroissant.

Voici la pile d’appels pour C(3,7,1,1) :

On déduit de la fonction terminale la fonction itérative. Il suffit de faire un Tant Que la condition d’arrêt n’est pas atteinte.

c – On a déjà la relation récursive dans l’énoncé.

Voici l’arbre d’appels pour C(2,4) :

Exercice 6
On définit la fonction de McCarthy comme suivant :

Que fait la fonction pour n>100 ? pour n=98, 99, 100 ? En général pour n<=100 ?
On va faire un peu de mathématique… Si n > 100 on aura n-10. Le problème se pose quand on commence avec n<=100. Calculer pour 98, 99 et 100. On va faire une démonstration directe.
Pour n entre 90 et 100 compris – soit 11 valeur consécutive, ça nous servira plus tard. On fera Carthy(Carthy(n+11)) donc on dépassera la valeur de 100. Donc on aura Carthy(n+1) au final. Si n+1 n’est toujours pas supérieur à 100, on remet le couvert. Donc on s’arrête quand on passera de 100 à 101, or Carthy(101)=101-10=91.
En reprend ce qu’on a laissé au début du précédent paragraphe. Sur les 11 dernières valeurs consécutives, on aura un résultat de 91. On note que tout nombre entre 0 et 89, auquel on rajoute 11 tant que c’est inférieur à 90 aura une valeur finale entre 90 et 100 compris.
On en déduit que Carthy sur une valeur de 100 ou moins donnera la valeur de 91.
Il fallait bien un peu de mathématique. L’informatique n’est qu’une autre façon syntaxique de faire des maths !
Exercice 7
On parle de récursivité croisée lorsque deux fonctions s’appellent l’une l’autre récursivement.
On va tester sur une récursivité croisée pour savoir si un nombre est pair (vrai) ou impair (faux). Voici la proposition :

Testez pour pair(2), impair(3), pair(3) et impair(2). L’algorithme est-il correct ? Sinon le changer pour vérifier la correction ← P.S: si le prof demande ça c’est que l’algo a un problème CQFD
Evidemment l’algo n’est pas correct. Prenons pair(3) → impair(2) → pair(1) → impair(0) → pair(-1) → impair(-2) → etc. C’est que les conditions d’arrêts ne marchent que si le nombre de la méthode pair est pair et la méthode impair est impair. On va seulement changer la méthode impair.

A vous de retester si c’est correct maintenant !
Pour avoir un algorithme plus solide, il faudrait vérifier que l’entier en entrée soit positif (ou alors faire la valeur absolue).
Dans le cas d’une entrée avec un double ou flottante, il est possible de le rendre entier en l’arrondissant. Pour cela, il faut connaitre le chiffre après la virgule avec le calcul suivant virgule=n*10[10]. Si virgule<5 alors on cast (entier)n, sinon on cast (entier)n+1.
Exercice 8
Il est impossible de conclure sur le récursif sans parler des fameuses Tours de Hanoï (la hantise des étudiants et parfois aussi des chargés de TD et prof !). On va donc s’y prendre doucement.

On dispose de n plateaux de taille différentes, et de 3 tiges, numérotées de 0 à 2.
Initialement, tous les plateaux sont situés sur la tige i. Le but est de les transférer sur la tige j, en respectant les règles suivantes :
– On ne peux déplacer qu’un plateau à la fois.
– Les plateaux doivent toujours rangés par taille décroissante sur une tige (le plus grand en bas puis par ordre décroissant en remontant sur la tige).
1 – Résolvez le problème à la main si n = 2, i = 0 et j = 2 (donc 2 plateaux, ils sont tous de base sur la tige 0 et on veut les mettre sur la tige 2).
2 – Résolvez le problème à la main si n = 3, i = 0 et j = 2 (donc 3 plateaux, ils sont tous de base sur la tige 0 et on veut les mettre sur la tige 2).
3 – Supposez qu’un de vos amis sache résoudre le problème pour un certain n, et n’importe quels i et j. On vous demande de résoudre le problème pour n + 1. Vous avez le droit d’utiliser l’aide de votre ami. Comment vous y prenez-vous ?
4 – Ecrire la fonction récursive qui permet de résoudre ce problème pour tous n, i, j (Si vous y arrivez sans tricher félicitation ! Sinon c’est normal on est presque tous passé par ce grand moment d’incompréhension et de remise en cause de sa carrière…)
1 –
On transfère le petit plateau de 0 à 1.
On transfère le grand plateau de 0 à 2.
On transfère le petit plateau de 1 à 2.
2 –
On transfère le petit plateau de 0 à 2.
On transfère le plateau moyen de 0 à 1.
On transfère le petit plateau de 2 à 1. (on a déplacé 2 plateaux de 0 vers 1).
On transfère le grand plateau de 0 à 2.
On transfère le petit plateau de 1 à 0.
On transfère le plateau moyen de 1 à 2.
On transfère le petit plateau de 0 à 2. (on a déplacé 2 plateaux de 1 vers 2).
3 –
On déplacer n plateaux de i à l’emplacement qui n’est ni i ni j (par les séries de trois manipulations du point 2). On déplace ensuite le dernier plateau (le plus gros) de i à j. On remet à contribution l’ami pour déplacer les n plateaux vers j.
4 –
Si vous trouvez ça… champagne ! On va renommé pour plus de facilité les tiges en d pour celle de départ, a pour celle d’arrivé et r pour celle qui reste

Regardons son fonctionnement, voici la structure générale de l’algorithme :
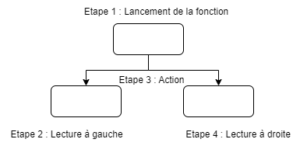
Prenons par exemple Hanoi(2,d,a,r), notons l’ensemble des récursions avec l’ordre de base (d,a,r) même si cela n’a pas de sens d’un poids de vue récursif :
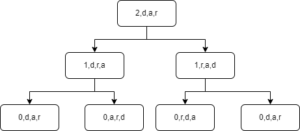
Notons que les noeuds ayant une valeur n de 0 ne servent à rien car la fonction sera vide.
Prenons maintenant l’arbre avec l’ordre des actions. Pour parcourir l’arbre ne faisons un parcours d’arbre

Un noeud réalise son action lorsque nous passons en dessous :
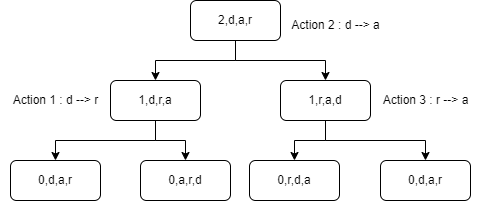
Ce qui donnerait les déplacements suivant :
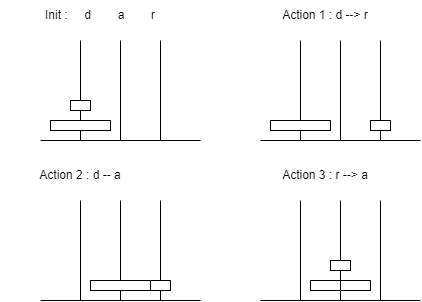
Exercice 9
Écrivez un programme pour trouver le PGCD de deux nombres en utilisant la récursivité.
Voici l’idée derrière l’algorithme :
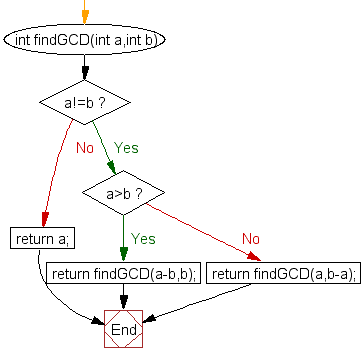
Ce qui donne l’algorithme suivant :

Il est aussi possible de faire directement le modulo (plutôt que a-b plusieurs fois) pour faire une récursion avec le reste :

Exercice 10
Écrivez un programme pour convertir un nombre décimal en binaire en utilisant la récursivité.
Voici l’idée derrière l’algorithme :
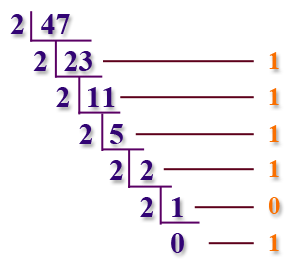

Exercice 11
Écrivez un programme pour trouver le LCM de deux nombres en utilisant la récursivité.

En voici l’algorithme :
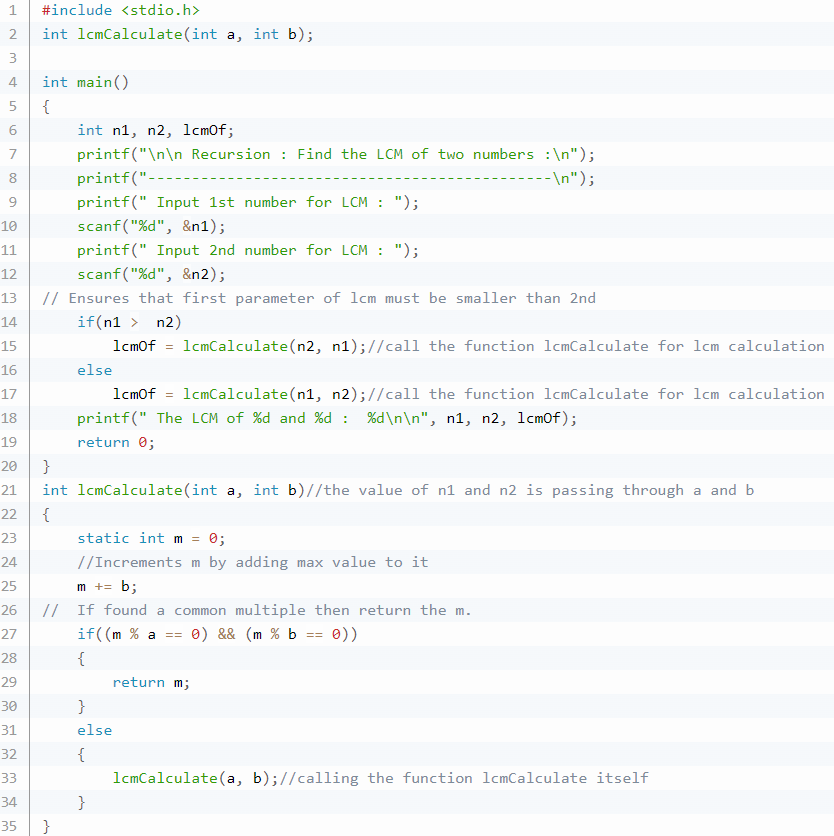
La fonction récursive lcm() prend deux entiers comme argument. Prenez une variable statique m et initialisez-la avec zéro, puis mettez à jour avec l’un des nombres. Ici, nous mettons à jour la variable m avec b, donc la variable m sera toujours divisible par la variable b. Par conséquent, nous devons vérifier uniquement avec la variable a, c’est-à-dire (m%a == 0).
Puisque nous ajoutons le plus grand nombre à la variable m, la variable b doit donc contenir le plus grand nombre. Lors de l’appel de lcm(), nous devons transmettre le plus petit nombre comme a et le plus grand nombre comme b.
Si nous ajoutons le plus grand nombre, le nombre d’appels récursifs sera le minimum, mais si nous ajoutons le plus petit nombre, le nombre d’appels récursifs sera supérieur à celui du cas précédent. Nous savons que moins d’appels récursifs donnent des performances élevées.
Prenons l’exemple des nombres 3 et 7. Si nous ajoutons le plus grand nombre 7 à la variable somme alors,
0+7 = 7 (appel depuis la fonction principale), 7%3 != 0
7+7 = 14 (premier appel récursif), 14%3 != 0
14+7 = 21 (deuxième appel récursif)
21 est divisible par 3 et par 7
Il n’y aura donc que 2 appels récursifs.
De même, si l’on prend le plus petit nombre (3) alors,
0+3 = 3 , 3%7 != 0
3+3 = 6 , 6%7 != 0
6+3 = 9 , 9%7 != 0
9+3 = 12 , 12%7 != 0
12+3 = 15 , 15%7 != 0
15+3 = 18 , 18%7 != 0
18+3 = 21
21 est divisible par 3 et par 7
Il y aura donc 6 appels récursifs.
Exercice 12
Écrivez un programme pour vérifier si une chaîne donnée est Palindrome ou non.
Exercice 13
Le nombre Pi peut être calculé par la formule suivante :
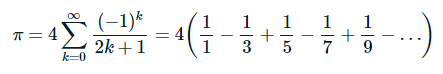
Ecrire un algorithme récursif permettant de calculer la valeur de Pi en considérant la séquence jusqu’au rang n.
Faire de même avec les approximations de Pi suivants.
Série de Gregory-Leibniz :

Et les séries plus anciennes de Madhava, Ramanujan, David et Chudnovsky (la factorielle sera un appel récursif à part entière) :

Voici l’algorithme en récursif :
gregory(n)
{
si(n==0) retourner 4
retourner 4*pow(-1,n)/(2*n+1)+gregory(n-1)
}
Les autres formules suivent le même principe, inutile de tout détailler. Attention tout de même à utiliser le bon calcul dans la récursion ! (les algorithmes seront plus facile à écrire en récursif non terminal.
Exercice 14
Dans les années 1920, Wilhelm Ackermann et Gabriel Sudan, alors étudiants sous la direction de David Hilbert, étudient les fondements de la calculabilité. Sudan est le premier à donner un exemple de fonction récursive mais non récursive primitive, appelée alors fonction de Sudan. Peu après et indépendamment, en 1928, Ackermann publie son propre exemple de fonction récursive mais non récursive primitive. À l’origine, Ackermann considère une fonction ϕ(m, n, p) dépendante de trois variables.
Une fonction de seulement deux variables est donnée plus tard par Rózsa Péter et Raphael Robinson ; c’est cette dernière qui est connue aujourd’hui sous le nom de fonction d’Ackermann.
La fonction d’Ackermann-Péter est définie récursivement comme suit :

La fonction grandit tellement vite qu’il est rapidement impossible de l’écrire avec un nombre classique et qu’il faut utiliser la notation de Knuth !

La solution est très simple, mais je vous déconseille de lancer l’algorithme sur un PC.
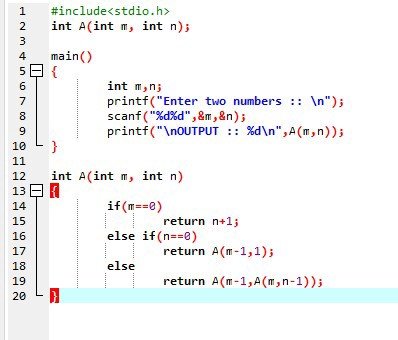
Exercice 15
Voici la fonction de Sudan, autre élève de David Hilbert. Cette fonction a été conçu en 1927 donc une année plus tôt que la fonction d’Ackermann.
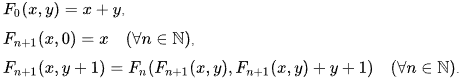
Ici, plus la valeur de n grandit, plus le résultat de la fonction de la fonction explose. En voici l’example pour F_1(14,14).
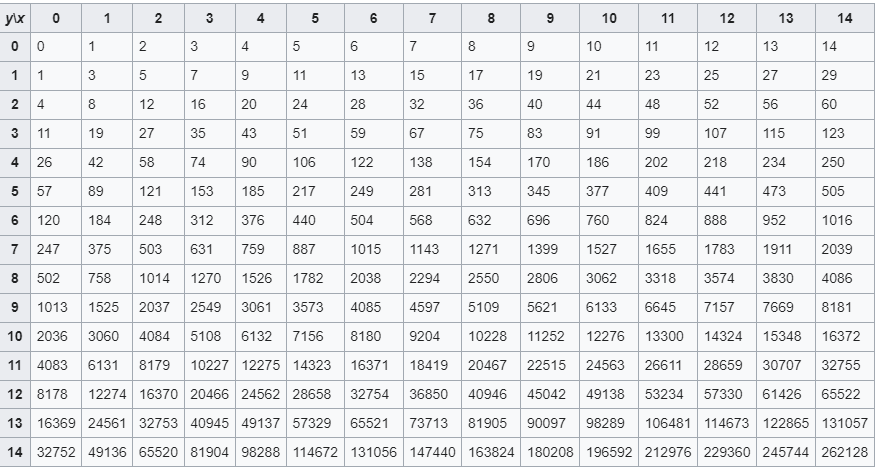
Rien de bien compliqué, il suffit de recopier la formule mathématique sous forme de récursion.

Exercice 16
La fonction de Takeuchi, abrégée tak ou parfois tarai, est la présentation récursive d’une fonction qui doit son nom à Ikuo Takeuchi (竹内郁雄). La présentation de la fonction, qui, par ailleurs, admet une définition non récursive assez simple, peut requérir des calculs très longs si le compilateur qui l’implante n’est pas performant. Pour cette raison, elle est souvent utilisée pour tester les performances de l’implantation des fonctions récursives par le compilateur d’un langage de programmation.
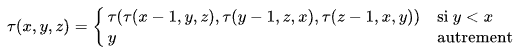
La définition originale de Takeuchi était la suivante :

tarai est l’abréviation de « passer autour » en japonais. John McCarthy a nommé cette fonction tak() d’après Takeuchi.
La récursivité à été amélioré grâce à une récursivité croisée :

Exercice 17
La séquence Male-Female Hofstadter est définie par :
F(0)=1, M(0)=0 et
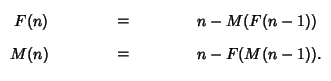
Ecrire un algorithme récursif permettant de calculer la séquence de Hofstadter.
De même pour la séquence G :

Il s’agit d’un algorithme récursif croisé (aussi dit parfait).

Pour la séquence G, le principe est le même :

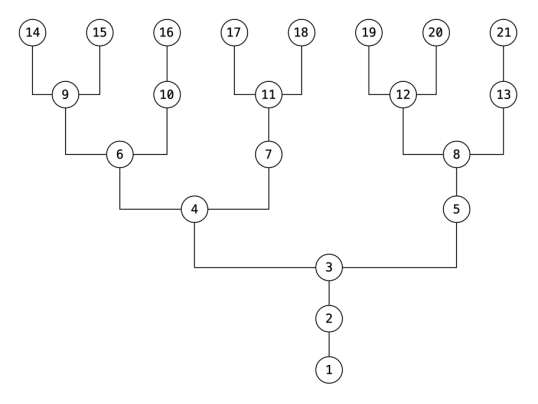
Vous trouverez ci-dessous un exemple d’arbre de nœuds formé lorsque le programme est exécuté avec des valeurs de n comprises entre 1 et 21. Par exemple, G(15) produira la valeur 9, et G(9) produira la valeur 6, etc. Il est intéressant de noter que la séquence de Fibonacci est visible sur le côté droit de l’arbre.
Exercice 18
Certains langages de programmation permettent la mémoïsation. Il s’agit d’une mise en cache des valeurs de retour d’une fonction selon ses valeurs d’entrée. Le but de cette technique d’optimisation de code est de diminuer le temps d’exécution d’un programme informatique en mémorisant les valeurs retournées par une fonction.
Ainsi, en réalisant la suite de Fibonacci, il est possible de se mémoriser les valeurs déjà calculées afin d’éviter de saturer la mémoire avec des valeurs déjà obtenu dans une autre branche de l’arbre d’appel.
En fait, chaque fois que nous calculons fib (i), nous pourrions simplement mettre en cache ce résultat et l’utiliser plus tard. Ainsi, lorsque nous appelons fib (n), nous ne devrions pas avoir à faire beaucoup plus que 0 (n) appels, car il n’y a que O(n) valeurs possibles que nous pouvons lancer sur fib(n).

Ici l’arbre de récursion sera bien différent de celui de la variante non terminale :
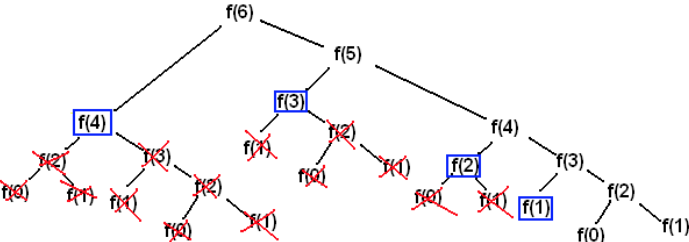
Notez que l’arbre ci-avant ne prend pas compte du sens d’appel gauche puis d’appel droit. Pour plus de confort, il est coutume de mettre le premier appel en fils gauche et le deuxième en fils droit, donc le contraire de l’arbre présenté !
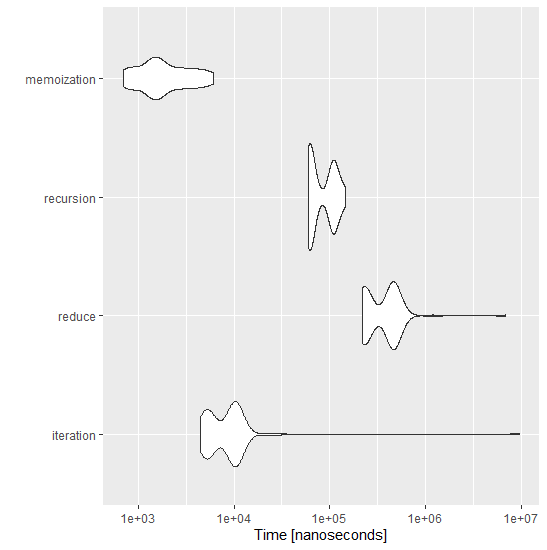
Les temps de calcul s’en retrouvent grandement diminué comme le montre le schéma suivant sur Fibo(100) sous ses variantes :
Exercice 19
Certains langages de programmation permettent la mémoïsation. Il s’agit d’une mise en cache des valeurs de retour d’une fonction selon ses valeurs d’entrée. Le but de cette technique d’optimisation de code est de diminuer le temps d’exécution d’un programme informatique en mémorisant les valeurs retournées par une fonction.
Ecrire un algorithme calculant factoriel n (n!) utilisant le principe de mémoïsation.
Voici la solution classique pour faire le calcul factoriel en récursif :

L’implémentation non mémorisée ci-dessus, étant donné la nature de l’algorithme récursif impliqué, nécessiterait n + 1 invocations de factorielles pour arriver à un résultat, et chacune de ces invocations, à son tour, a un coût associé en termes de temps nécessaire à la fonction. pour renvoyer la valeur calculée. Selon la machine, ce coût peut être la somme de :
Le coût de configuration du cadre de pile d’appels fonctionnel.
Le coût pour comparer n à 0.
Le coût pour soustraire 1 de n.
Le coût de configuration du cadre de pile d’appels récursifs. (Comme ci-dessus.)
Le coût pour multiplier le résultat de l’appel récursif à factoriel par n.
Le coût de stockage du résultat renvoyé afin qu’il puisse être utilisé par le contexte appelant.
Dans une implémentation non mémorisée, chaque appel de niveau supérieur à factorial inclut le coût cumulé des étapes 2 à 6 proportionnel à la valeur initiale de n.
Une version mémorisée de la fonction factorielle suit :

Dans cet exemple particulier, si factorial est d’abord invoqué avec 5, puis invoqué ultérieurement avec une valeur inférieure ou égale à cinq, ces valeurs de retour auront également été mémorisées, puisque factorial aura été appelé de manière récursive avec les valeurs 5, 4, 3, 2, 1 et 0, et les valeurs de retour pour chacune d’entre elles auront été stockées. S’il est ensuite appelé avec un nombre supérieur à 5, comme 7, seuls 2 appels récursifs seront effectués (7 et 6), et la valeur pour 5 ! aura été stocké à partir de l’appel précédent.
De cette manière, la mémorisation permet à une fonction de devenir plus efficace en termes de temps à mesure qu’elle est appelée plus souvent, ce qui entraîne une éventuelle accélération globale.
Exercice 20
Et voici un petit exercice mêlant tout ce que vous avez pu voir récursivité, croisé et mémoïsation.
Il y a n oranges dans la cuisine et vous avez décidé de manger quelques-unes de ces oranges tous les jours comme suit :
- Mangez une orange.
- Si le nombre d’oranges restantes n est divisible par 2 alors vous pouvez manger n/2 oranges.
- Si le nombre d’oranges restantes n est divisible par 3 alors vous pouvez manger 2*(n/3) oranges.
Vous ne pouvez choisir qu’une seule des actions par jour.
Étant donné l’entier n, renvoie le nombre minimum de jours pour manger n oranges.
Entrée : n = 10
Sortie : 4
Explication : Vous avez 10 oranges.
Jour 1 : Mangez 1 orange, 10 – 1 = 9.
Jour 2 : Mange 6 oranges, 9 – 2*(9/3) = 9 – 6 = 3. (Puisque 9 est divisible par 3)
Jour 3 : Mange 2 oranges, 3 – 2*(3/3) = 3 – 2 = 1.
Jour 4 : Mangez la dernière orange 1 – 1 = 0.
Il faut au moins 4 jours pour manger les 10 oranges.


