Contenus
ToggleArbres couvrants
Afin de minimiser le coût des réseaux électriques, des connexions de câblage, de la tuyauterie, de la reconnaissance vocale automatique, etc., nous utilisons des algorithmes qui construisent progressivement un arbre couvrant (ou plusieurs de ces arbres) comme étapes intermédiaires du processus de recherche des arbres couvrants minimum.
L’Internet et de nombreux autres réseaux de télécommunication ont des liens de transmission qui relient les nœuds ensemble dans une topologie maillée qui inclut certaines boucles. Afin d’éviter les boucles de pont et les boucles de routage, de nombreux protocoles de routage conçus pour de tels réseaux exigent que chaque routeur se souvienne d’un arbre couvrant.
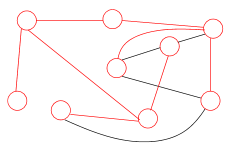
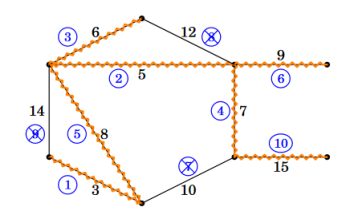
Il est facile de construire un arbre couvrant :
- tant qu’on a pas ajouter n-1 arêtes à G’, avec n le nombre de sommets du graphe, on choisit une arête de G de telle façon que son ajout ne crée pas un cycle dans G’.
- tant que le nombre d’arêtes restantes est supérieur à n-1, on retire une arête de G tel que G soit toujours connexe.
La problématique des arbres couvrants est très utilisée dans le cadre d’arêtes pondérées.
Pour fabriquer un arbre couvrant de poids minimal, nous énoncerons deux algorithmes gloutons.
Algorithme de Kruskal
Au début, le graphe G’ ne contient que les sommets de G et nous possédons une file (fifo) vide f :
- pour chaque sommet v de G
- ajouter v à f
- trier f par ordre croissant
- tant que la file n’est pas vide
- défiler f -> arête a
- si l’ajout de a ne crée pas de cycle dans G’ alors ajouter a dans G’
- retourner G’
Pour savoir si l’on crée un cycle, il suffit de savoir si l’on peut atteindre un sommet de l’arête en partant de l’autre sommet dans G’. Pour rappel, dans un arbre il n’existe qu’un seul chemin d’un sommet à un autre.
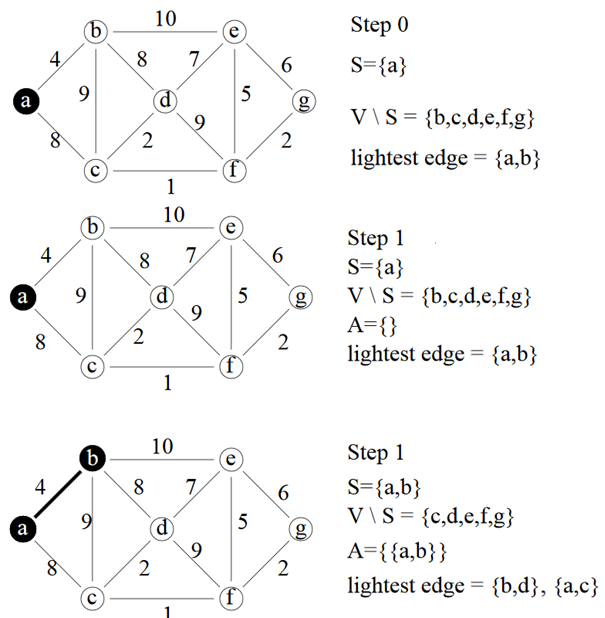
Algorithme de Prim
Le principe consiste à agrandir un arbre en ajoutant une arête de poids minimum incidente à l’arbre.
Au début, le graphe G’ ne contient qu’un sommet de G :
- tant que G’ ne contient pas tous les sommets de G
- mettre dans une file toutes les arêtes de G qui relient un sommet de G’ à un sommet qui n’est pas dans G’
- trier par ordre croissant la file
- tant que la file n’est pas vide ou qu’on n’a pas rajouté d’arête
- défiler la file -> arête a
- si l’ajout de a ne crée par de cycle dans G’ alors ajouter a dans G’
L’algorithme étant complexe à comprendre par l’écrit, nous allons montrer un exemple :

Kruskal pas à pas
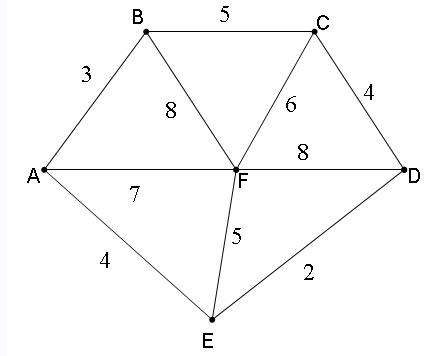
Ci-dessous la liste des arêtes triées par ordre de poids :
| Arête | ED | AB | CD | AE | BC | EF | CF | AF | BF | FD |
| Poids | 2 | 3 | 4 | 4 | 5 | 5 | 6 | 7 | 8 | 8 |
______________

Pas de cycle détecté
| Arête | ED | AB | CD | AE | BC | EF | CF | AF | BF | FD |
| Poids | 2 | 3 | 4 | 4 | 5 | 5 | 6 | 7 | 8 | 8 |
______________
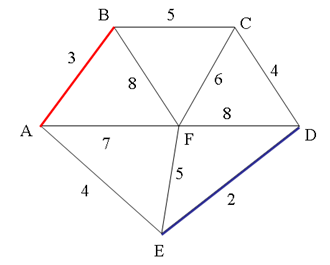
Pas de cycle détecté
| Arête | ED | AB | CD | AE | BC | EF | CF | AF | BF | FD |
| Poids | 2 | 3 | 4 | 4 | 5 | 5 | 6 | 7 | 8 | 8 |
______________
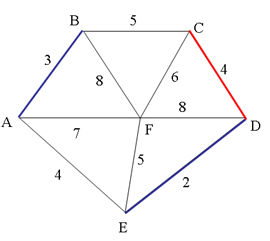
Pas de cycle détecté
| Arête | ED | AB | CD | AE | BC | EF | CF | AF | BF | FD |
| Poids | 2 | 3 | 4 | 4 | 5 | 5 | 6 | 7 | 8 | 8 |
______________
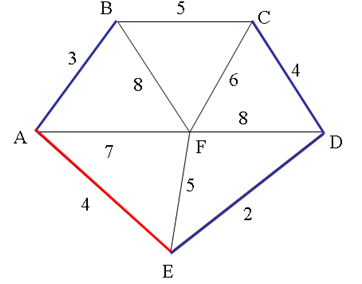
Pas de cycle détecté
| Arête | ED | AB | CD | AE | BC | EF | CF | AF | BF | FD |
| Poids | 2 | 3 | 4 | 4 | 5 | 5 | 6 | 7 | 8 | 8 |
______________

| Arête | ED | AB | CD | AE | BC | EF | CF | AF | BF | FD |
| Poids | 2 | 3 | 4 | 4 | 5 | 5 | 6 | 7 | 8 | 8 |
- Cycle détecté: ne pas utiliser BC
Pas de cycle détecté, n-1 arête-> END
| Arête | ED | AB | CD | AE | BC | EF | CF | AF | BF | FD |
| Poids | 2 | 3 | 4 | 4 | 5 | 5 | 6 | 7 | 8 | 8 |
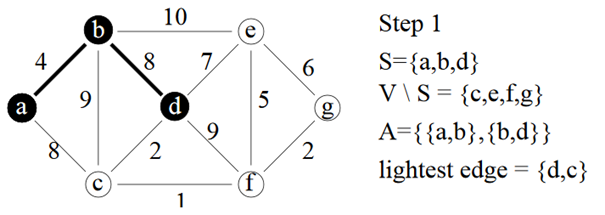
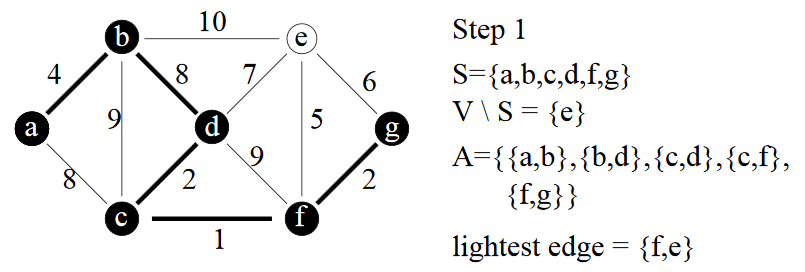
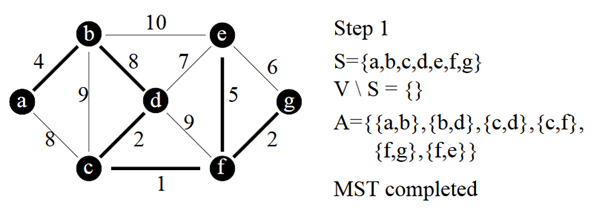
Prim pas à pas