Contenus
ToggleAlgorithme de Ford-Bellman
Le problème des plus courts chemins à partir d’une origine n’a de solution que s’il n’existe pas de circuit absorbant atteignable. L’algorithme de Ford-Bellman vérifie qu’il n’existe pas de circuit absorbant atteignable à partir de s. Si c’est le cas, il retourne les plus courts chemins à partir de s. L’algorithme de Ford-Bellman est un algorithme de programmation dynamique gourmand qui calcule les chemins les plus courts de taille croissante. Il convient à n’importe quel graphe.
Conditions.
- Cas général
Au départ, la distance est initialisée à 0 pour l’origine et à l’infini pour les autres sommets.

On va examiner tous les arcs et améliorer si possible la valeur des chemins. La nouvelle valeur pour chaque sommet est la distance minimale de tous les chemins de taille k-1 auxquels on rajoute les arêtes entrant dans le sommet. Comme il peut y avoir des circuits, il faut recommencer.
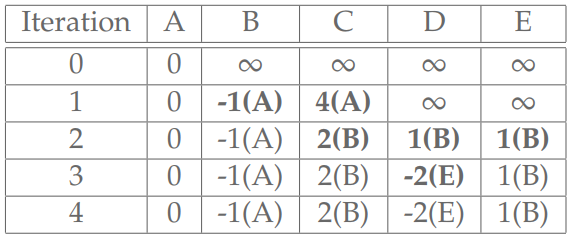

Pour des raisons pratiques, la résolution du l’algorithme de Ford-Bellman ne retourne qu’un vecteur. Ce qui correspond à une colonne courante du tableau présenté.
Optimalité.
Le chemin le plus court de l’origine à lui-même est de 0. Puis les chemins de taille 1 sont calculés de telle sorte que nous ne gardons que le plus court chemin de l’origine à tout autre sommet.
l’algorithme calcule les plus courts chemins des chemins de taille k (pour l’itération k) à partir des plus courts chemins des chemins de taille k-1, il est donc optimal quelle que soit l’itération d’arrêt de l’algorithme.
S’il n’y a pas ce circuit absorbant, un plus court chemin est nécessairement élémentaire. On est donc sûr qu’un plus court chemin doit alors être trouvé en au plus n-1 étapes de l’itération. Si une valeur de D est améliorée, c’est qu’il y a un circuit absorbant.
pour chaque sommet u du graphe
d[u, 0] = +∞
d[s, 0] = 0
pour k = 1 jusqu'à Nombre de sommets - 1 faire
pour chaque arc (u, v) du graphe faire
d[v, k] := min(d[v, k-1], d[u, k-1] + poids(u, v))
fin
fin
retourner dExemple
Prenons pour exemple le graphe suivant :
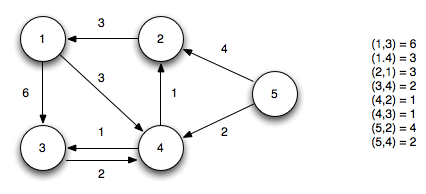
Prenons le noeud 5 comme source, puis on initialise les autres distances à l’infini. Le vecteur π représente les prédécesseurs.

Itération 1: Les arcs (u5,u2) et (u5,u4) sont relaxés, on met à jour les distances et les prédécesseurs.
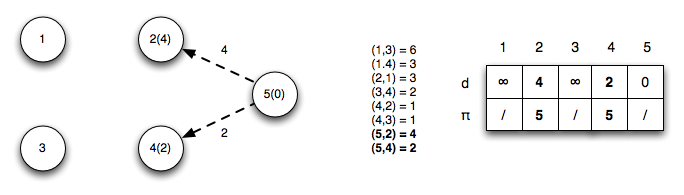
Itération 2: Les arcs (u2,u1), (u4,u2) et (u4,u3) sont relaxés, on met à jour les distances aux noeuds 1, 2, et 4. Notons que (u4,u2) trouve un plus court chemin vers 2 en passant par le noeud 4.

Itération 3: Les arcs (u2,u1) sont relaxés (car on a trouvé un chemin plus court pour aller au noeud 2 dans la dernière itération).

Itération 4: Aucun arc n’est relaxé.

Les chemins les plus courts partant du noeud 5 sont :
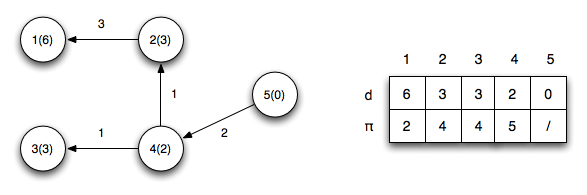
L’algorithme se présente sous la forme d’un tableau comme ci-dessous :
| Iteration | 1 | 2 | 3 | 4 | 5 |
| 0 | inf | inf | inf | inf | 0 |
| 1 | inf | 4(5) | inf | 2(5) | 0 |
| 2 | 7(2) | 3(4) | 3(4) | 2(5) | 0 |
| 3 | 6(2) | 3(4) | 3(4) | 2(5) | 0 |
| 4 | 6(2) | 3(4) | 3(4) | 2(5) | 0 |
Les distances en rouge montre les noeuds qui ont subi un changement dans l’itération courante. Pour l’itération suivante il faut donc relaxé les arcs provenant de ces noeuds. L’algorithme s’arrête lorsqu’il n’y a plus de changement.
